Пример выполнения задания № 1.
Преобразование исходной схемы представлено на рис. 10-12.
Рис.
10. Объединение звеньев
и
в звено и объединение
и
звеньев
и в звено,
где
=
,
=
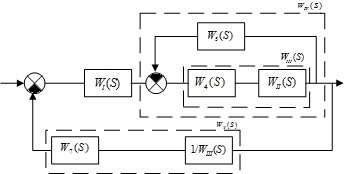
Рис.
11. Объединение звеньев
и
в
звено
,
объединение звеньев
и
в
звено
,
перенос линии связи за звено
и объединение звеньев
и 1/
в
звено , где
=
,
,
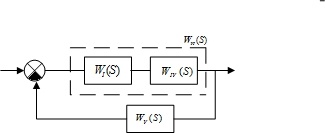
Рис.
12. Объединение звеньев
и
в звено
и
объединение
звеньев
и
в звено
,
где
=
,
После преобразований получили передаточную функцию разомкнутой системы в общем виде:
,
и в числовом виде:
Дале получили передаточная функция замкнутой системы в общем виде:
,
и в числовом виде:
.
Характеристическое уравнение имеет вид:
.
Для того что бы построить годограф Михайлова необходимо найти действительную и мнимую части характеристического уравнения, заменим S на j:
,
где,
действительная часть
,
а
мнимая часть:
.
После преобразований схемы и получения необходимых значений, построим годограф Михайлова, в разных масштабах (рис. 13-17).
Рис.13. Часть годографа Михайлова в 1 квадранте
Рис. 14. Часть годографа Михайлова в 1,2 и 3 квадранте
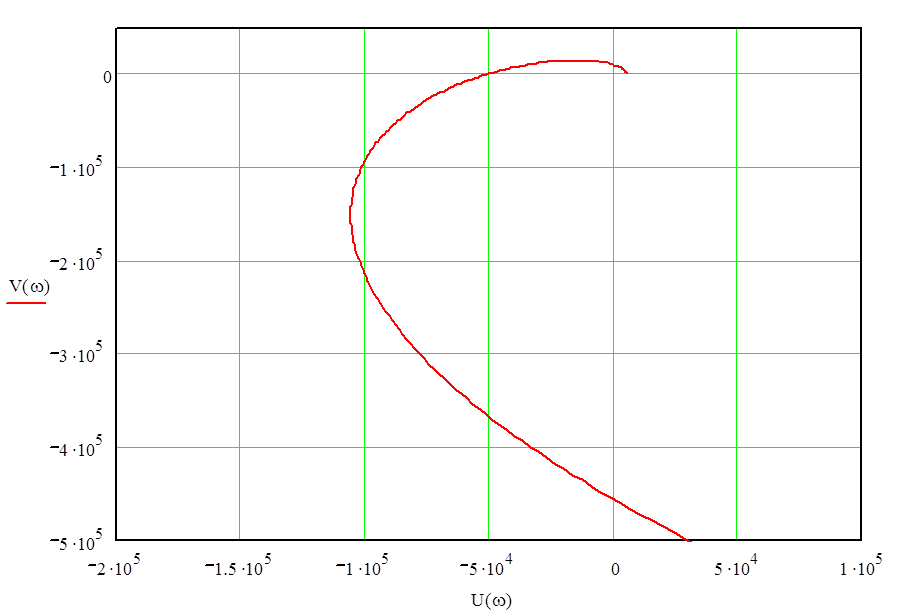
Рис. 15. Часть годографа Михайлова в 1,2,3 и 4 квадранте
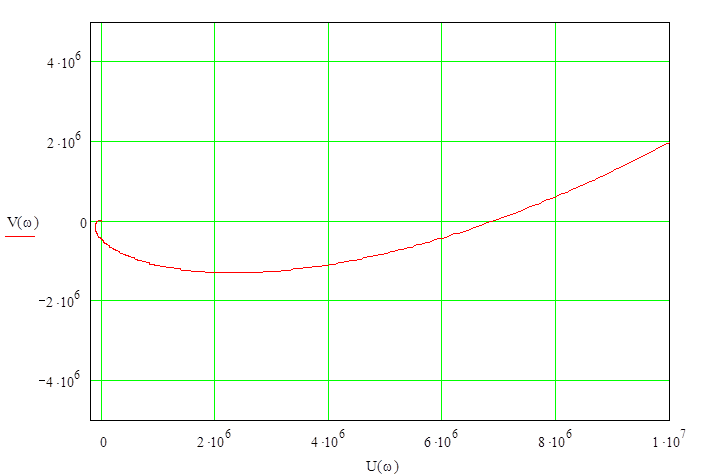
Рис. 16. Часть годографа Михайлова в 3,4,5 квадранте
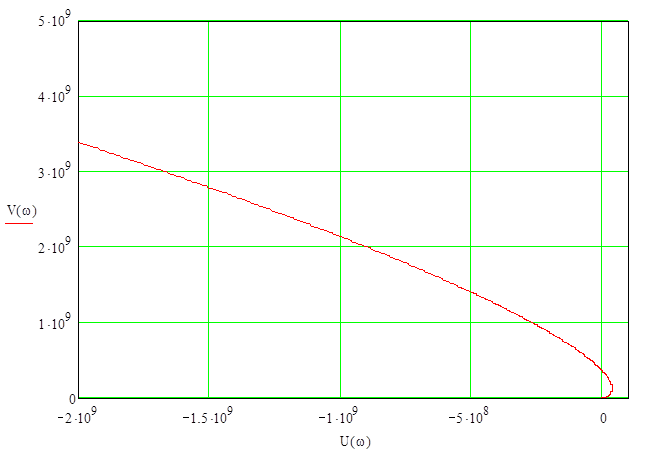
Рис. 17. Часть годографа Михайлова в 5, 6 квадранте
Вывод: данная замкнутая система является устойчивой, так как годограф Михайлова начинается на положительной части вещественной оси и проходит последовательно против хода часовой стрелки, не попадая в начало координат 6 квадрантов (характеристическое уравнение 6 порядка).
Пример выполнения задания № 2.
Для суждения об устойчивости замкнутой системы по критерию Найквиста необходимо определить передаточную функцию разомкнутой системы, поэтому необходимо преобразовать исходную систему к общему виду, то есть произвести преобразование цепи.
Преобразование производилось по следующему принципу: так как элементы исходно цепи соединены последовательно, то их заменяем одним элементом, имеющим передаточную функцию равной произведению всех трех передаточных функций исходной цепи, то есть: W=W1*W2*W3. Если использовать математический вид полученной передаточной функции, то он выглядит так:
.
Для того, чтобы применить критерий Найквиста необходимо построить амплитудно-фазовую частотную характеристику. Этот можно реализовать, заменив в формуле для передаточной функции преобразованной системы р на j. Далее разделим на действительную и мнимую части передаточную функцию преобразованной системы: W(j)=U()+jV(),
где
,
.
Теперь можно построить график амплитудно-фазовой частотной характеристики. Полученная зависимость представлена на рис. 18.
Согласно критерию Найквиста, замкнутая система будет устойчива, если амплитудно-фазовая частотная характеристика разомкнутой системы не охватывает точку (-1,0). Анализируя полученный результат, устанавливаем, что полученная нами кривая не охватывает точку (-1,0), следовательно, система устойчива.
Далее определим запас устойчивости, используя график представленный на рис. 18. Запасом по модулю |М| является отрезок, начало которого находится в точке пересечения кривой с осью абсцисс, а конец – точка (-1,0). Длина этого отрезка и будет являться запасом по модулю. В нашем случае М=0,31. Запас по фазе Δφ равен: Δφ=π-|φ(wi)|. В нашем случае запас по фазе составляет примерно -11˚ (рис. 19).
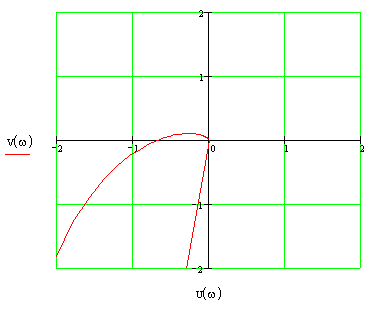
Рис. 18. Амплитудно-фазовая частотная характеристика
М
Рис. 19. Запасы устойчивости по критерию Найквиста
Далее необходимо провести расчет запасов по амплитуде и по фазе, используя логарифмическую зависимость амплитуды от частоты и фазовую зависимость (рис. 20). Система является устойчивой, так как при ()=0, 20log(A())<0, а при 20log(A())=0, ()>0.
М
Рис. 20. Логарифмическая амплитудная и фазовая частотные
характеристики
Для анализа запасов устойчивости, определим точку пересечения логарифмической амплитудной зависимости с нулевым уровнем. При =5,716, 20log(A())=0. Далее подставив найденное значение в формулу описывающую фазовую зависимость, получим, что запас по фазе составляет 0,199 рад. или 11,4˚.
Для нахождения запаса по амплитуде, необходимо определить точку пересечения фазовой зависимости с уровнем 0, т.е. определить при которой ()= 0, в данном случае =7,07. Далее подставив найденное значение в формулу для логарифмической амплитудной характеристики, получим значение запаса устойчивости по амплитуде в децибелах: 20log(A(7,07))= - 3,519.