Вычислить интегралы

1. Ответ:

2. Ответ:

3. Ответ:

4.

.

5. Ответ:

6. Ответ:

7. .

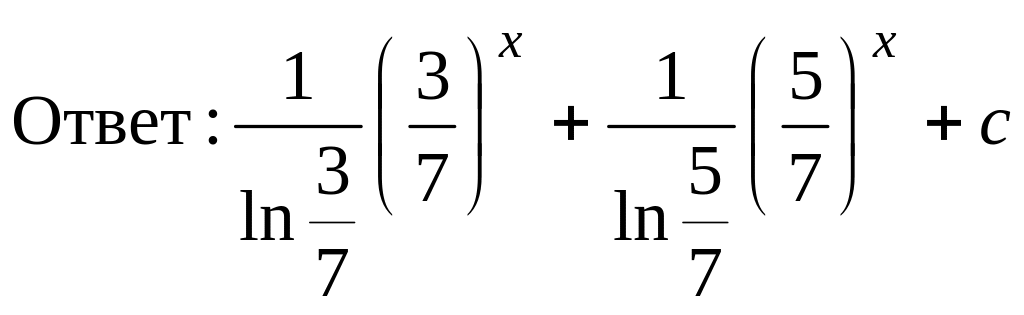Занятие 2. Интегрирование по частям

Пример 2.1. Вычислить интеграл

Решение. Положим здесь u=lnx, dv=dx, откуда du=dx/x и v=x.

Применяя формулу интегрирования по частям, получим:

Пример 2.2. Вычислить интеграл

Решение. Положим u=x², dv=e^xdx, откуда du=2xdx, v=e^x.

Применяя формулу интегрирования по частям, получим

Для вычисления опять применим формулу

интегрирования по частям. Положим откуда

Подставляя, находим

Пример 2.3. Вычислить интеграл

Решение. Здесь после интегрирования по частям получим в правой части тот же интеграл, что и в левой. Решая полученное уравнение относительно интеграла, находим значение интеграла.

Значит,

Отсюда

И окончательно имеем

Вычислить интегралы:

Занятие 3. Интегралы от функций, содержащих

квадратный трехчлен

Рассмотрим интегралы вида:

Для отыскания указанных интегралов от функций, содержащих квадратный трехчлен, для преобразования их к формулам интегрирования, следует в начале выделить полный квадрат из квадратного трехчлена.

Пример 3.1. Вычислить интеграл

Решение. Выделим из квадратного трехчлена полный квадрат

:

Сделаем замену: Получаем:

Пример 3.2. Вычислить интеграл

Решение. Выделим из квадратного трехчлена полный кварат

и заменим переменную х, полагая .Тогда получим dx=dt, 7-8x=1-8t и

Далее разложим полученный интеграл на два слагаемых, соответственно двум слагаемым в числителе, и находим по формулам

Возвращаясь к переменной х, окончательно получим

Пример 3.3. Вычислить интеграл

Решение. Выделим из трехчлена полный квадрат

.

Записав d (x-2) вместо dx и интегрируя, найдем

Пример 3.4. Вычислить интеграл

Решение. Выделяем из трехчлена полный квадрат:

и вводим новую переменную z =x-1. Тогда получим: dz= dx,

Разложив полученный

интеграл на два интеграла,

,

Находим каждый из них отдельно:

Подставляя найденные интегралы I₁ и I₂ и возвращаясь к переменной х, получим

Вычислить интегралы.

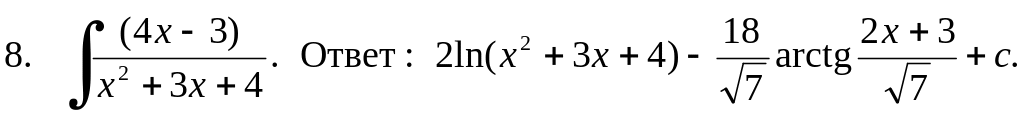
Занятие 4. Интегрирование рациональных дробей

Пример 4.1. Вычислить интеграл

Решение. Разложим знаменатель на множители. Замечая,

что х₁=-1, х₂=1, х₃=-2, х₄=2 являются корнями многочлена

Поэтому подынтегральную функцию разложим на такие простейшие дроби

Приводим равенство (1) к общему знаменателю и отбрасываем его

Отсюда, перемножив и приведя подобные члены, будем иметь

Приравняв коэффициенты при одинаковых степенях х в обеих частях тождества, получим систему уравнений для определения коэффициентов A, B, C, D :

Решив систему, получим:

Таким образом, мы получили разложение рациональной дроби на простейшие:

Интегрируя, получим:

.

Замечание. Часто нахождение коэффициентов разложения значительно упрощается, если применить так называемый метод произвольных значений. Рассмотрим с этой точки зрения только что приведенный пример.

Полученное в этом примере равенство (2) есть тождество, справедливое при любом значении х. Поэтому выберем четыре (по количеству неизвестных коэффициентов) значения х таким образом, чтобы каждое обратило в нуль какой-нибудь из сомножителей в примере такими значениями являются корни знаменателя х₁=1, х₂=-1, х₃=2, х₄=-2.

Подставив поочередно эти значения в равенство (2), получим:

при х=-1 имеем: 4=A·(-2)·1·(-3)+B∙0+C∙0+D∙0, то есть А=2/3;

при х=1 имеем: 2=A·0+B·2 правой части равенства (2).

В нашем ·3·(-1)+C·0+D·0, то есть В=-1/3;

при х=-2 имеем: 8=A·0+B·0+C·(-1)(-3)-4)+D·0, то есть С=-2/3;

при х=2 имеем: 4=A·0+B·0+C·0+D·3·1·4, то есть D=1/3.

На практике указанный метод наиболее целесообразно применять в случае, когда знаменатель Q(x) правильной рациональной дроби имеет вещественные корни.

Пример 4.2. Вычислить интеграл

Решение. Разложение на простейшие дроби имеет вид

Приводим правую часть к общему знаменателю и приравниваем числители

(3)

Полагая последовательно х=0, х=2, х=-1, находим, что A=1/2, С=1/36, D=2/3. Подставляя эти значения в (3) и раскрывая скобки, получим:

Приравнивая коэффициенты при х³ и х, получим

, откуда

Таким образом,

Пример 4.3. Вычислить интеграл

Решение. Знаменатель не имеет вещественных корней. Разложение данной правильной дроби на простейшие имеет вид:

Приводим дроби в правой части равенства к общему знаменателю и приравниваем числители:

Приравнивая коэффициенты при одинаковых степенях х, в левой и правой частях равенства, будем иметь:

Отсюда, решая систему, получим:

откуда

и

Вычислить интегралы:

4.

Занятие 5. Интегрирование тригонометрических функций

I.Рассмотрим интегралы вида

где m и n – целые положительные числа.

Эти интегралы берутся с помощью тригонометрических формул

Пример 5.1. Вычислить интеграл

Решение. Так как,

то

II. Рассмотрим интегралы вида

где т, п – целые числа.

Интегралы таких типов можно свести к формулам интегрирования, руководствуясь следующими правилами:

1. Интегралы от четной степени синуса или косинуса можно найти путем понижения степени по формулам

2. Интегралы от нечетной степени синуса или косинуса можно найти путем отделения от нее одного множителя и замены кофункции новой переменной.

3. Интегралы вида (2) можно найти по правилу 1, если т и п оба четные, или по правилу 2, если т или п (или и т, и п) нечетно.

4. Интегралы вида (2) можно найти с помощью замены tgx=t или ctgx = t, если оба показателя т и п четные, причем хотя бы один из них отрицателен.

5. С помощью замены tgx = t или ctgx = t можно найти интегралы вида (2), если т и п – целые отрицательные числа одинаковой четности.

6. Интегралы вида (3) также можно найти с помощью замены tgx=t или ctgx=t.

Пример 5.2. Вычислить интеграл

Решение. Преобразуем подынтегральную функцию:

Таким образом,

Пример 5.3.Вычислить интеграл

Решение. Преобразуем подынтегральное выражение:

Сделаем замену cosx= t, тогда –sinxdx=dt. Таким образом,

Возвращаясь к переменной х, окончательно получим

Пример 5.4. Вычислить интеграл

Решение. Преобразуем подынтегральное выражение:

Сделаем подстановку tgx=t, тогда

Возвращаясь к переменной х, окончательно получим

Вычислить интегралы.

Занятие 6. Интегрирование тригонометрических функций (продолжение)

Рассмотрим интегралы вида

Интегралы данного вида преобразуются в интегралы от рациональных функций подстановкой

Для этого с помощью равенства (*) выражаем: cosx, sinx и х через t, а также dx через t и dt:

Подстановка (*) называется универсальной тригонометрической подстановкой. Иногда вместо