Гоувпо “Воронежский государственный технический университет “

Кафедра робототехнических систем

Методические указания

к выполнению контрольных работ № 1 - 2

по дисциплине “Теория автоматического управления”

для студентов специальностей

151001 “Технология машиностроения”,

151002 “Металлорежущие станки и комплексы”, 150201 “Машины и технология обработки металлов давлением”

очной формы обучения

Воронеж 2011

Составители: канд. техн. наук А.П. Харченко,

канд. техн. наук В.В. Кольцова

УДК 612.313

Методические указания к выполнению контрольных работ № 1-2 по дисциплине “Теория автоматического управления” для студентов специальностей 151001 “Технология машиностроения”, 151002 “Металлорежущие станки и комплексы”, 151201 “Машины и технология обработки металлов давлением” очной формы обучения/ ГОУВПО ”Воронежcкий государственный технический университет”; сост. А.П.Харченко, В.В. Кольцова. Воронеж, 2011. 16 с.

В методических указаниях представлены варианты контрольных работ. Контрольные работы содержат вопросы по типовым динамическим звеньям, структурным схемам, переходным процессам с различными типами регуляторов.

Предназначены для студентов 3-4 курса.

Методические указания подготовлены в электронном виде в текстовом редакторе MS Word 7.0 и содержатся в файле метТAUkr. doc.

Табл. 5 . Библиогр.: 4 назв.

Рецензент канд. техн. наук, доц. В.А. Трубецкой

Ответственный за выпуск зав. кафедрой д-р техн. наук, проф. А.И. Шиянов

Издается по решению редакционно-издательского совета

Воронежского государственного технического университета

© ГОУВПО «Воронежский государственный

технический университет», 2011

Контрольная работа № 1

ПЕРЕХОДНЫЕ ПРОЦЕССЫ НА ВЫХОДЕ

МАТЕМАТИЧЕСКОЙ МОДЕЛИ РЕДУКТОРА

1. Теоретические сведения

В теории автоматического управления передаточная функция (ПФ) или иногда называемая в моделировании технических систем математическая модель (ММ) находится из уравнения (уравнение элемента или системы в операторной форме, где символ производной d/dt заменен оператором р или переменной s, а символ интегрирования ∫dt заменен величиной обратной 1/ р или 1/s), как отношение выходного сигнала элемента Yвых(p) к входному сигналу Хвх(р).

Передаточные функции редуктора, как типового динамического звена при заданных входных сигналах определяется тремя видами:

Пропорциональное звено

W(p) = Y(p) / X(p) = Ω2(p) / Ω1(p) = K1.

Интегрирующего звена

W(p) = Y(p) / X(p) = 1/p * [Ψ2(p) / Ω1(p) ] = K2 / p.

Дифференцирующего звена

W(p) = Y(p) / X(p) = p*Ω2(p) / Ψ1(p) = K3 *p,

где Y(p), X(p) – символическое изображение выхода и входа модели редуктора; Ω2(p), Ω1(p) – символическое обозначение скорости вращения выходного и входного вала редуктора; Ψ1(p), Ψ2(p) - символическое обозначение перемещения выходного и входного вала редуктора; К1-К3 – значения коэффициента передачи редуктора, как, пропорционального, интегрирующего и дифференцирующего звеньев;

В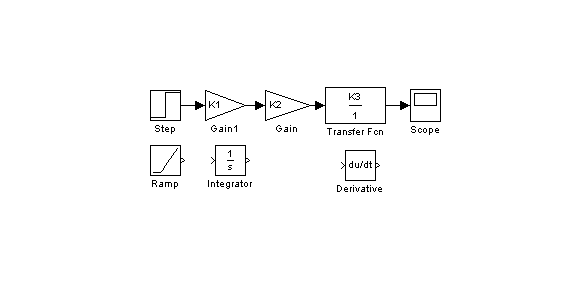 теории автоматического управления для исследования ММ элементов и систем используются следующие типовые входные сигналы.

Ступенчатый единичный сигнал

Х1(t) = К*1(t),

где К– амплитуда ступенчатого сигнала.

Линейный сигнал

Х2(t) = К*t,

где К – крутизна линейного сигнала.

Нелинейный сигнал

Х3(t) = К*t²/2,

где К – коэффициент нелинейного сигнала.

Переходная функция h(t) ( ее график – переходная характеристика ) на выходе редуктора при ступенчатом входном сигнале 1(t) (временные функции y(t) на выходе редуктора при линейном и нелинейном входных сигналах x(t) ) определяется выражениями, поученными из уравнения пропорционального, интегрирующего и дифференцирующего типовых динамических звеньев при заданном входном сигнале.

Ступенчатая функция

h1(t) = K1*1(t).

Линейная функция

h2(t) = K2*t.

Нелинейная функция

h3(t) = K3*t²/2.

2. Методические указания к выполнению контрольной работы

2.1. Варианты заданий параметров временных функций на выходе модели 1-го и 2-го редуктора приведены в табл.1.

2.2. Выбрать передаточную функцию или математическую модель 1-го и 2-го редуктора.

2.3. Определить тип входного сигнала 1-го и 2-го редукторов.

Входные типовые сигналы для моделей 1-го и 2-го редукторов могут быть одинаковые или разные.

2.4. Записать выражение для выбранных входного сигнала Х1(t) 1-го и Х2(t) 2-го редукторов для получения заданных временных функций на выходе 1-го h1(t) и на выходе 2-го h2(t).

2.5. Записать выражение для заданной временной функции на выходе модели 1-го h1(t) и 2-го h2(t) редуктора.

В табл. 1 используются следующие обозначения временных функций и коэффициентов передачи моделей:

В – вариант задания;

С1, С2 – ступенчатая функция на выходе 1-го и 2-го редуктора;

Л1, Л2 – линейная функция на выходе 1-го и 2-го редуктора;

Н1, Н2 – нелинейная функция на выходе 1-го и 2-го редуктора;

О1, О2 – функция, расположенная по осям h и t, на выходе 1-го или 2-го редуктора

Кс1, Кс2 – коэффициент передачи ступенчатой функции 1-го и 2-го редуктора;

Кл1, Кл2 – коэффициент передачи линейной функции 1-го и 2-го редуктора;

Кн1, Кн2 – коэффициент передачи нелинейной функции 1-го и 2-го редуктора;

Ко12 – коэффициент передачи функции по осям h и t.

2.6. Изобразить графически в выбранном масштабе временные характеристики y(t) или h(t) моделей 1-го и 2-го редуктора.

Представить форму и параметры типового входного сигнала Х1(t) и Х2(t) в выбранном масштабе и изобразить в том же масштабе форму заданной временной функции h1(t) и h2(t) для выбранных моделей 1-го и 2-го редуктора.

Параметры временной функции на выходе модели 1-го и 2-го редуктора

Таблица 1

В

С1

Л1

Н1

О1

С2

Л2

Н2

02

Кc1

Кл1

Кн1

Кс2

Кл2

Кн2

Ко12

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

1

-

–

+

–

+

–

–

–

–

–

30

0.7

–

–

–

2

–

+

–

–

–

–

–

+

–

3

–

–

–

–

2

3

–

–

+

–

–

+

–

–

–

–

3

–

12

–

–

4

–

+

–

–

–

–

–

+

–

5

–

–

–

–

4

5

–

–

+

–

–

–

–

+

–

–

2

–

–

–

1

6

–

–

+

–

–

+

–

–

–

–

15

–

0.9

–

–

7

–

–

+

–

+

–

–

–

–

–

0.5

2

–

–

–

8

–

+

–

–

–

–

–

+

–

1

–

–

–

–

3

9

–

–

+

–

–

+

–

–

–

–

4

–

11

–

–

10

–

+

–

–

+

–

–

–

–

2

–

8

–

–

–

11

–

–

+

–

–

–

–

+

–

–

0.5

–

–

–

5

12

–

–

+

–

–

+

–

–

–

–

0.1

–

0.5

–

–

13

–

–

+

–

+

–

–

–

–

–

5

12

–

–

–

14

–

+

–

–

–

–

–

+

–

0.7

–

–

–

–

6

15

–

–

+

–

–

+

–

–

–

–

2

–

7

–

–

16

–

+

–

–

+

–

–

–

–

4.5

–

9

–

–

–

17

–

–

+

–

+

–

–

–

–

–

0.1

0.5

–

–

–

18

–

+

–

–

+

–

–

–

–

2.5

–

7

–

–

–

19

–

–

+

–

–

–

–

+

–

–

3.2

–

–

–

7

20

–

–

+

–

–

+

–

–

–

–

0.2

–

1

–

–

21

–

–

+

–

+

–

–

–

–

–

0.7

3

–

–

–

22

–

+

–

–

–

–

–

+

–

0.6

–

–

–

–

1.5

23

–

–

+

–

–

+

–

–

–

–

2

–

10

–

–

24

–

+

–

–

+

–

–

–

–

0.3

–

0.6

–

–

–

25

–

–

+

–

–

–

–

+

–

–

6

–

–

–

2.5

26

–

–

+

–

–

+

–

–

–

–

1

–

4

–

–

27

–

–

+

–

+

–

–

–

–

–

6

5

–

–

–

28

–

+

–

–

–

–

–

+

–

0.5

–

–

–

–

3.5

29

+

–

–

–

–

–

+

–

2

–

–

–

–

4

–

30

+

–

–

–

–

+

–

–

4

–

–

–

2

–

–

31

+

–

–

–

–

+

–

6

–

–

–

–

2

–

1 Продолжение табл. 1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

32

–

+

–

–

–

–

–

+

–

60

–

–

–

–

4.5

33

–

–

–

+

–

+

–

–

–

–

–

–

3

–

5.5

34

+

–

–

–

–

–

+

–

3

–

–

–

–

6

–

35

–

–

–

+

–

+

–

–

–

–

–

–

50

–

6.5

36

+

–

–

–

–

+

–

–

50

–

–

–

30

–

–

37

+

–

–

–

–

–

+

–

60

–

–

–

–

50

–

38

–

–

+

–

–

–

–

+

–

–

–

–

–

40

7.5

39

–

+

–

–

–

–

–

+

–

10

–

–

–

–

8

40

+

–

–

–

–

–

+

–

8

–

–

–

–

30

–

41

+

–

–

–

–

+

–

–

10

–

–

–

6

–

–

42

–

–

–

+

–

–

+

–

–

–

–

–

–

8

9

43

–

–

+

–

–

–

–

+

–

–

20

–

–

–

10

44

+

–

–

–

–

+

–

–

30

–

–

–

20

–

–

45

+

–

–

–

–

–

+

–

20

–

–

–

–

48

–

46

–

+

–

–

–

–

–

+

–

16

–

–

–

–

12

47

–

–

–

+

–

+

–

–

–

–

–

–

28

–

14

48

–

–

+

–

–

–

–

+

–

–

12

–

–

–

16

49

–

+

–

–

+

–

–

–

–

18

–

14

–

–

–

50

+

–

–

–

–

+

–

–

32

–

–

–

28

–

–

51

–

–

+

–

–

–

–

+

–

–

16

–

–

–

8.5

52

–

–

–

+

–

–

+

–

–

–

–

–

–

12

18

53

–

+

–

–

+

–

–

–

–

22

–

24

–

–

–

54

+

–

–

–

–

–

+

–

16

–

–

–

–

14

–

55

–

+

–

–

–

–

–

+

–

24

–

–

–

–

20

56

–

–

+

–

–

–

–

+

–

–

24

–

–

–

22

57

–

–

–

+

–

+

–

–

–

–

–

–

30

–

24

58

+

–

–

–

–

+

–

–

22

–

–

–

24

–

–

59

–

+

–

–

–

–

–

+

–

14

–

–

–

–

26

60

–

–

+

–

–

–

–

+

–

–

26

–

–

–

28

61

–

–

–

+

–

–

+

–

–

–

–

–

–

16

30

62

+

–

–

–

–

+

–

–

24

–

–

–

18

–

–

63

–

+

–

–

+

–

–

–

–

6

–

8

–

–

–

64

–

–

+

–

+

–

–

–

–

–

22

28

–

–

–

Контрольная работа № 2

ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ

ПОСЛЕДОВАТЕЛЬНОГО, ПАРАЛЛЕЛЬНОГО И ВСТРЕЧНО-ПАРАЛЛЕЛЬНОГО СОЕДИНЕНИЙ ТИПОВЫХ

ДИНАМИЧЕСКИХ ЗВЕНЬЕВ