2. Свойства однородных полупроводников

2.1. Вывести закон действующих масс для концентраций основных и неосновных носителей в полупроводнике, предполагая, что для носителей тока в зоне проводимости и в валентной зоне, так же как для классических свободных частиц, применима ста­тистика Максвелла − Больцмана и что функция плотности состояний параболическая для обеих зон. Эффективные массы (для электронов) и (для дырок) считать известными и постоянными.

Решение. В любом полупроводнике равновесные концентрации электронов п₀ (в зоне проводимости) и дырок р₀ (в валентной зоне) можно записать в виде

(2.1)

(2.2)

где f₀(ξ) − функция распределения Ферми − Дирака

(2.3)

Функции плотности состояний g_c(ξ) для зоны проводимости и g_v(ξ) для валентной зоны можно аппроксимировать функциями плотности состояний свободной частицы:

(2.4)

(2.5)

Интегралы в выражениях (2.1) и (2.2) берутся соответственно по зоне проводимости и валентной зоне.

Из выражений (2.1) и (2.2) следует, что величины п₀ и р₀ могут трактоваться как площади областей под кривыми f₀(ξ)g_c(ξ) и [1 − f₀(ξ)]g_v(ξ) (см. заштрихованные области на рис. 2.1).

Рис. 2.1. Распределение электронов и дырок в

полупроводнике

На рис. 2.1 эти кривые приведены для трех случаев: образец «почти собственного» полупроводника (п₀ ≈ р₀), образец сильнолегированного полупроводника п-типа (п₀ >> р₀), образец сильнолегированного полупроводника p-типа (п₀ << р₀).

Из приведенных графиков видно, что уровень Ферми должен располагаться около середины запрещенной зоны для образцов с проводимостью, близкой к собственной (если бы это было не так, то п₀ и р₀ не были бы приблизительно равными).

Из аналогичного рассуждения следует, что в образце n-типа уровень Ферми должен быть выше, а в образце p-типа − ниже, чем в образце с почти собственной проводимостью. Заметим также, что если образец содержит лишь небольшое количество донорных или акцепторных примесей, уровень Ферми должен быть на несколько kT дальше от края ближайшей зоны. (Вспомним, что kT = 1/40 эВ при 300 °К, Δξ = ξ_c − ξ_υ = 0,72 эВ для Ge и 1,15 эВ для Si.)

При таких условиях для каждого значения энергии в зоне проводимости (ξ – ξ_F)/kT >> 1 и для каждого значения энергии в валентной зоне (ξ_F – ξ)/kT >> 1. Это означает, что для зоны проводимости (ξ > ξ_c)

(2.6)

а для валентной зоны

(2.7)

Эти выражения означают, что при описанных выше условиях распределение Ферми − Дирака электронов в зоне проводимости и дырок в валентной зоне можно очень хорошо аппроксимировать распределением Максвелла − Больцмана (2.6) и (2.7).

Подставим выражения (2.4) и (2.6) в (2.1) и (2.5), а (2.7) в (2.2). При этом пределы для интеграла по зоне проводимости следует выбрать так: от дна зоны проводимости ξ_c до +∞, и для интеграла по валентной зоне – от −∞ до ξ_υ (потолка валентной зоны). Тогда, соответственно изменяя начало отсчета энергий для п₀ и р₀, получим выражения

(2.8)

(2.9)

где

x_c = (ξ – ξ_c)/kT, x_υ = (ξ_υ – ξ)/kT. (2.10)

Верхний предел интеграла по зоне проводимости мы взяли рав­ным +∞, а не действительной энергии, соответствующей вер­шине зоны проводимости; возникающая при этом погрешность невелика, поскольку значение функции распределения f₀(ξ) с увеличением ξ уменьшается так быстро, что в любом случае сколько-нибудь значительный вклад в интеграл дает лишь часть зоны проводимости. Аналогично можно объяснить, почему за нижний предел интеграла для валентной зоны выбрана −∞.

Интегралы в выражениях (2.8) и (2.9) можно оценить с помощью таблиц или заметив, что каждый интеграл сводится к гамма-функции . Подставляя эту величину, можно получить

(2.11)

(2.12)

где

(2.13)

Согласно (2.11), (2.12) и (2.13) произведение п₀р₀ (при фиксированной температуре) имеет постоянное значение

(2.14)

где Δξ = ξ_c − ξ_υ − ширина запрещенной энергетической зоны между зоной проводимости и валентной зоной. Это и есть закон действующих масс для полупроводников. Заметим, что прибли­жение Больцмана (и, следовательно, закон действующих масс) не выполняется, когда экспоненциальный множитель в (2.11) или в (2.12) равен единице или больше, т. е. когда n₀>U_с или p₀ > U_v. В германии и кремнии при комнатной температуре значения U_c и U_v порядка 10¹⁹ см^-3.

В собственном полупроводнике концентрации п₀ и р₀ равны. Подставляя п₀ = р₀ = п_i (п_i − концентрация электронов и дырок собственного полупроводника) в (2.14), получим

(2.15)

где

(2.16)

Концентрация носителей тока в собственном полупроводнике будет, очевидно, экспоненциальной функцией температуры с энер­гией активации Δξ/2.

2.2. Найти энергию Ферми для собственного полупроводника, принимая, что статистика Максвелла − Больцмана применима и для зоны проводимости, и для валентной зоны.

Решение. В общих выражениях (2.11) и (2.12) для п₀ и р₀ содержится также зависимость п₀ и р₀ от ξ_F. Однако для соб­ственного полупроводника п₀ = р₀ = n_i.

Приравнивая правые части выражений (2.11) и (2.12) и решая полученное уравнение относительно ξ_F с учетом (2.13), получаем

(2.17)

Отсюда ясно, что при уровень Ферми лежит в запре­щенной зоне посередине между краями зоны проводимости и валентной зоны; если то он смещается слегка вверх из этого положения, если , он смещается вниз.

Поскольку kT обычно много меньше ширины запрещенной зоны Δξ, то даже если одна эффективная масса много больше другой, смещение уровня Ферми от среднего положения между зонами (в масштабе энергии запрещенной зоны) будет не очень большим.

2.3. В полупроводнике, в котором все донорные и акцептор­ные атомы ионизованы, найти концентрации электронов п₀ и дырок р₀, выразив их через концентрации донорных и акцеп­торных примесей N_d, N_a и через концентрацию собственных носи­телей n_i.

Решение. В кристалле, который является электрически нейтраль­ным, полная сумма зарядов всех носителей и примесных ионов должна быть равна нулю. Если на единицу объема приходится N_d донорных атомов, из которых n_d не отдали свои электроны (и, следовательно, нейтральны), то оставшиеся N_d − n_d доноров (на единицу объема) будут ионизованы (следовательно, положи­тельно заряжены).

Аналогично на единицу объема приходится N_a − р_а отрица­тельно заряженных ионизованных акцепторов, где р_а − число акцепторных атомов, не захвативших электроны. Условие элек­тронейтральности можно тогда записать так:

e(p₀ – n₀ + N_d − n_d − N_a + р_а) = 0. (2.18)

Если же все доноры и акцепторы ионизованы, тогда n_d = p_a = 0, и равенство (2.18) примет вид

p₀ – n₀ + N_d − N_a = 0. (2.19)

Но согласно (2.15) где n_i определено соотношением (2.16). Подставляя в условие (2.19) и находя из него п₀, получим

(2.20)

В полученном решении квадратного уравнения знак радикала (корня) можно взять положительным, так как концентрация п₀ должна уменьшаться до + n_i, если N_d = N_a = 0.

Аналогично вместо п₀ можно подставить в (2.19) и решить полученное уравнение, что даст

(2.21)

Заметим, что если речь идет о заполнении уровней зоны про­водимости и валентной зоны носителями тока, то чистые кри­сталлы, в которых N_d = N_a = 0, и скомпенсированные кристаллы, в которых N_d = N_a ≠ 0, совершенно тождественны; в обоих слу­чаях п₀ = р₀ = n_i. Для сильнолегированных кристаллов n-типа (N_d − N_a >> n_i)

(2.22)

для сильнолегированных образцов p-типа (N_a – N_d >> n_i)

(2.23)

2.4. Показать, что в схеме опыта, показанной на рис. 2.2, на клеммах A и В появляется напряжение, которое соответствует электрическому полю при условии, что (эффект Холла).

Рис. 2.2. Образец p-типа в однородном магнитном поле B₀

Показать, что когда длина среднего свободного пробега не зависит от скорости, то

Решение. Выражение для y-компоненты электрического поля:

(2.24)

Так как зависящий от магнитного поля член в выражении для х-компоненты плотности тока

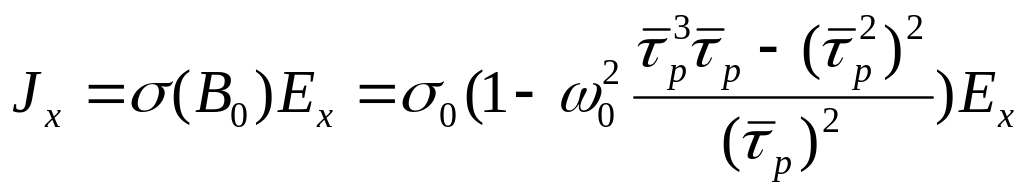(2.25)

мал по сравнению с σ₀ (по­скольку второй член в скобках порядка а ), то в первом приближении им можно пренебречь и записать

(2.26)

Подставляя (2.26) в (2.25) и выражая ω₀ через В₀ (2.27) и μ_p через (2.28),

(2.27)

(2.28)

получаем

(2.29)

где

(2.30)

Здесь с – скорость электрона.

Поле Е_у, пропорциональное произведению J_XB₀, называется полем Холла, а коэффициент пропорциональности R − коэффициентом Холла. Если средняя длина свободного пробега не зависит от скорости, то, согласно (2.31) и с учетом (2.32) и (2.33),

(2.31)

(2.32)

(2.33)

получим

(2.34)

Для примесного полупроводника n-типа рассуждения анало­гичны, разница лишь в знаке заряда. Это означает, что коэффици­ент Холла будет отрицателен, и его величина равна .

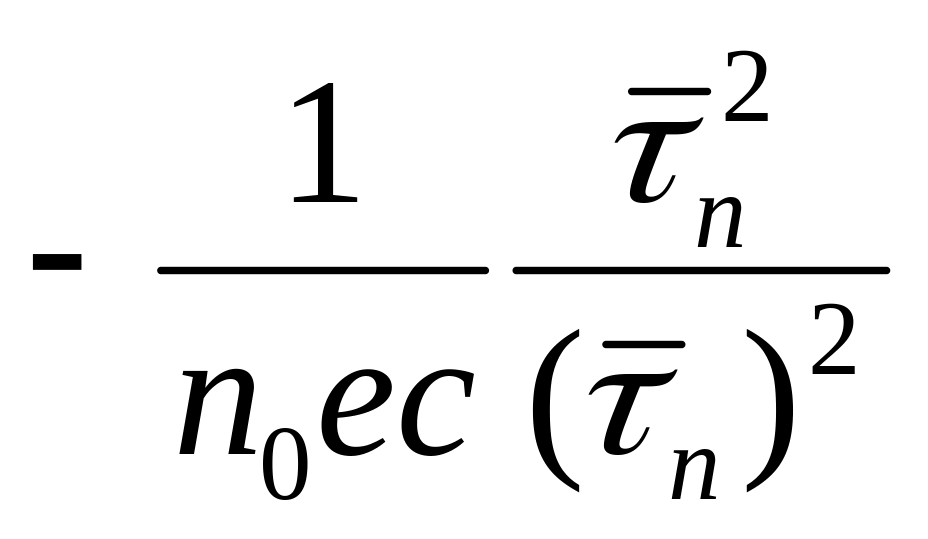Коэффициент Холла легко находится экспериментально из измерения напряжения Холла на клеммах A и B на установке типа изображенной на рис. 2.2. Это позволяет легко устано­вить, является ли образец полупроводником п- или p-типа, и определить концентрацию носителей заряда.