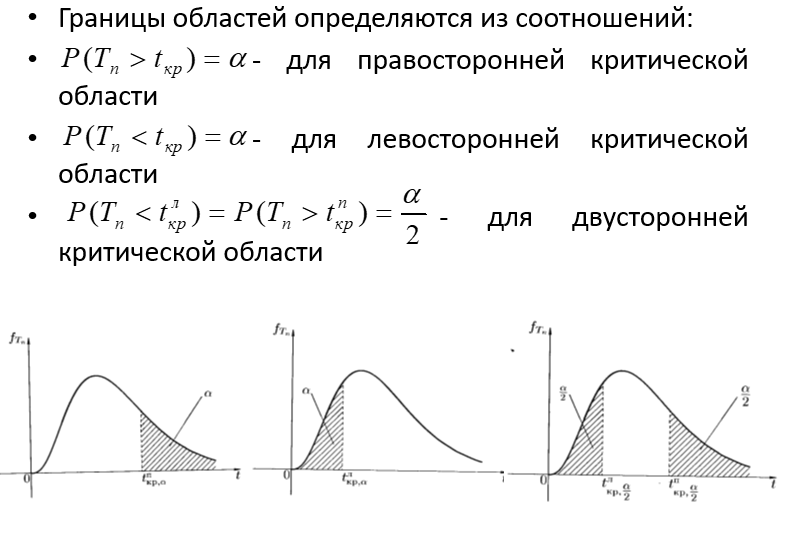
- •1 Раздел. Случайные события
- •Случайное событие. Достоверное событие. Невозможное событие.
- •Классическое и геометрическое определения вероятности.
- •Статистическое определение вероятности.
- •Аксиоматическое определение вероятности
- •Раздел 2. Одномерные случайные величины
- •Раздел 3. Двумерные случайные величины, функции от случайных величин, предельные теоремы
- •Раздел 4. Математическая статистика
- •Эмпирическая функция распределения
- •Критерий согласия - Пирсона
- •Критерий согласия Колмогорова
Эмпирическая функция распределения
Эмпирическая функция распределения (выборочная функция распределения) — естественное приближение теоретической функции распределения данной случайной величины, построенное по выборке. В отличие от эмпирической функции распределения выборки, функцию распределения F (x) генеральной совокупности называют теоретической функцией распределения.
Эмпирической функцией распределения (функцией распределения выборки) называют функцию, определяющую для каждого х относительную частоту события Х<х. где число вариант, меньших х, n - объем выборки.

Полигон частот
Полигон частот - графическое изображение статистического ряда (статистическая оценка неизвестного закона распределения).
Гистограмма

Выборочные квантили

Статистическая оценка

Статистическая оценка - некоторая функция от результатов наблюдений, предназначенная для статистического оценивания неизвестных характеристик и параметров распределения вероятностей
Свойства точечных оценок
То́чечная оце́нка в математической статистике — это число, оцениваемое на основе наблюдений, предположительно близкое к оцениваемому параметру.

Состоятельность оценки
Оценка параметра называется состоятельной, если она сходится по вероятности к оцениваемому параметру при
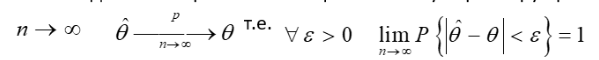
Т.е. с увеличением объема выборки качество оценки улучшается. Свойство состоятельности является обязательным для любого правила оценивания (несостоятельные оценки не рассматриваются).
Несмещенность оценки
Несмещённая оце́нка в математической статистике — это точечная оценка, математическое ожидание которой равно оцениваемому параметру.

Эффективность оценки

Метод моментов
Идея: приравнивание теоретических и выборочных моментов. Оценки, полученные данным методов не всегда эффективны.
Если необходимо оценить n параметров, то получим систему:
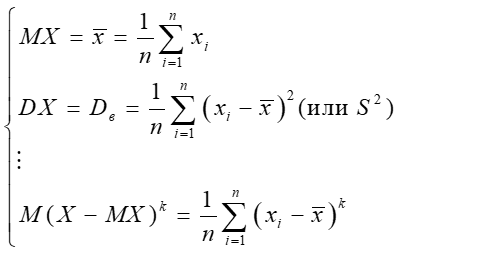
Если рассматривать не центральные моменты:
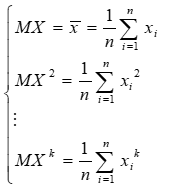
Метод максимального правдоподобия
Идея: найти максимум функции правдоподобия, т.е. подобрать такие значения параметров распределения, при которых выборка наиболее правдоподобна.
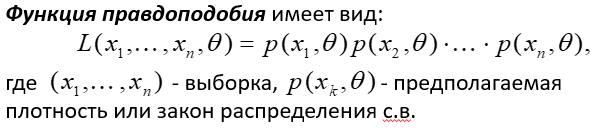
Если найти максимум этой функции, получим уравнение правдоподобия

Если оценивать n параметров, получим систему:
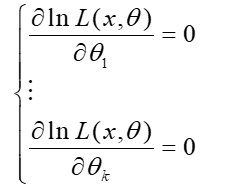
Интервальное оценивание
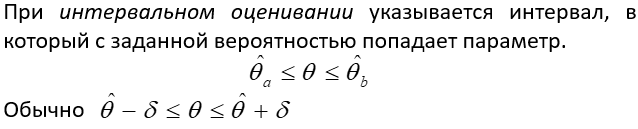
Этот интервал называется доверительным интервалом, а вероятность называется доверительной вероятностью или надежностью оценки (обозначается γ).
Уровень значимости при интервальном оценивании
Уровнем значимости оценки называется величина, равная α=1-γ
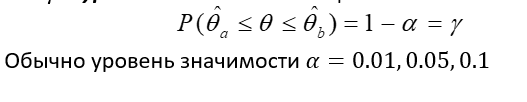
Статистическая гипотеза
Статистической гипотезой H 一 предположение относительно параметров или вида распределения случайной величины.
Статистические гипотезы делятся на:
параметрические гипотезы – гипотезы о параметрах распределения известного вида,
непараметрические гипотезы - гипотезы о виде неизвестного распределения .
Ошибки первого и второго рода при проверке гипотезы

Общая схема проверки гипотез
Проверка статистических гипотез может быть разбита на следующие этапы:
Располагая выборкой
 формулируют нулевую (H0)
и альтернативную (H1)
гипотезы;
формулируют нулевую (H0)
и альтернативную (H1)
гипотезы;Назначается уровень значимости α (обычно 0.1, 0.05, 0.01);
Выбирается тип/статистика критерия
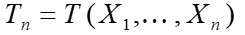 .
Обычно
это:
.
Обычно
это:
U - нормальное распределение;
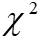 - распределение
x квадрат (Пирсона);
- распределение
x квадрат (Пирсона);t - распределение Стьюдента;
F - распределение Фишера-Снедекора.