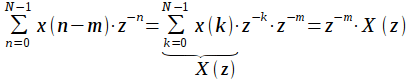- •Разностное уравнение и системная функция цф 1-го порядка
- •Структурная схема цф
- •Рассчитать и построить импульсную реакцию и ачх цф
- •1.3 Выполнение лабораторной работы
- •1.3.1 Исходные данные эксперимента
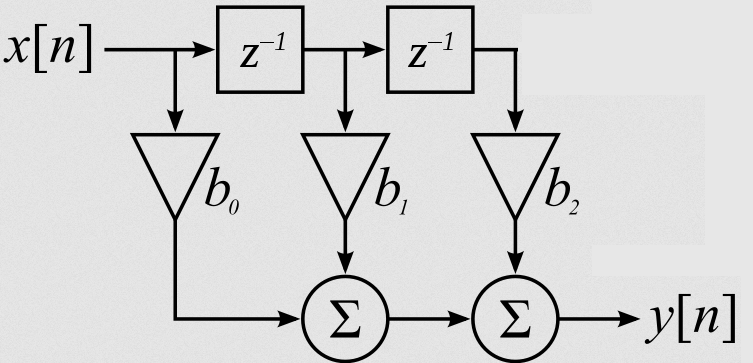
- •1.3.2 Структурная схема нерекурсивного цф 2-го порядка
- •1.3.3. Результаты лабораторного эксперимента
- •А) цф первого порядка:
- •Цф первого порядка:
- •Б) цф второго порядка:
- •1.4 Детальные выводы по проделанной работе.
- •1.4.1. Устойчивость.
- •1.4.2.Типы исследуемых фильтров.
- •1.4.3. Сравнение ачх нерекурсивных цф 1-го и 2-го порядка.
- •1.4.4. Преимущества нерекурсивных фильтров.
- •Контрольные вопросы:
- •Как определяется порядок цф?
- •При каком воздействии отклик цф называется переходной функцией?
- •Требуется ли проверять ких фильтр на устойчивость?
1.4.4. Преимущества нерекурсивных фильтров.
Нерекурсивные ЦФ обладают рядом преимуществ, а именно:
1) Нерекурсивные ЦФ являются всегда устойчивыми ввиду отсутствия полюсов в системной функции.
2) Возможность реализации линейной фазы нерекурсивных ЦФ.
3) Нерекурсивные ЦФ просты в реализации.
4) При реализации нерекурсивные ЦФ не требуют наличия цепей обратной связи.
Контрольные вопросы:
Запишите выражение для прямого Z-преобразования.
Переход
от оригинала
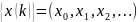 к изображению
к изображению
 определяемый равенством:
определяемый равенством:
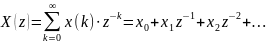
Называется z-преобразованием.
Чему равно Z-преобразование единичного импульса?
Z-преобразование единичного импульса есть точка на z-плоскости, поскольку функция не зависит от комплексной переменной z. Областью сходимости будет являться вся z-область.
Как называется отклик ЦФ на воздействие единичного импульса?
Импульсной характеристикой системы называется её реакция на единичный импульс при нулевых начальных условиях.
Свойства Z-преобразования.
Свойство
1.
Линейность. Z-образ суммы двух сигналов
равен сумме z-образов этих сигналов.
Действительно, пусть есть два дискретных
сигнала ![]() и
и ![]() ,
,![]() .
Найдем z-преобразование их суммы
.
Найдем z-преобразование их суммы![]() :
:
|
(11) |
Свойство
2.
Свойство задержки. Пусть дан исходный
дискретный сигнал
,
.
Найдем z-преобразование сигнала ![]() ,
задержанного на
,
задержанного на ![]() отсчетов:
отсчетов:
|
(12) |
При
выводе была введена переменная ![]() ,
тогда
,
тогда ![]() и
получили, что задержка исходного сигнала
на
добавляет
множитель
и
получили, что задержка исходного сигнала
на
добавляет
множитель ![]() к
z-преобразованию сигнала. Тогда задержка
на один отсчет соответствует
к
z-преобразованию сигнала. Тогда задержка
на один отсчет соответствует ![]() .
.
Свойство 3. Теорема о свертке. Пусть дано два сигнала и , . Найдем z-преобразование их круговой свертки.
|
(13) |
При выводе было использовано свойство задержки z-преобразования. Таким образом, z-преобразование свертки сигналов равно произведению их z-образов.
Как определяется порядок цф?
Порядок ЦФ определяется количеством реактивных элементов в цепи.
При каком воздействии отклик цф называется переходной функцией?
Импульсная переходная функция — выходной сигнал динамической системы как реакция на входной сигнал в виде дельта-функции Дирака. В цифровых системах входной сигнал представляет собой простой импульс минимальной ширины (равной периоду дискретизации для дискретных систем) и максимальной амплитуды.
Коэффициенты разностного уравнения ЦФ равны b0 = 1, b1 = 0.5. Чему равно численное значение импульсной реакции при n = 0?
1
Коэффициенты разностного уравнения ЦФ равны b0 = 1, b1 = 0.5, b2 = 0.8. Чему равно численное значение импульсной реакции при n = 1?
0.5
Требуется ли проверять ких фильтр на устойчивость?
Нет, не требуется, КИХ фильтр устойчив по сравнению с БИХ-фильтром. БИХ-фильтр будет устойчивым, если полюсы передаточной функции лежат внутри единичной окружности в z-плоскости.
На нерекурсивный ЦФ 2 порядка с коэффициентами b0=b1=b2=1 действует сигнал, состоящий из трех временных отсчетов: x(0)=x(1)=x(2)=1. Каково значение отсчета отклика фильтра y(2)?
yi=b0*xi+b1*xi-1+b2*xi-2
y(2)=b0*x2+b1*x1+b2*x0
y(2)=1+1+1=3
11) Как называется ЦФ, если все коэффициенты разностного уравнения ai=0?
Нерекурсивный.
12) Как определяется системная функция ЦФ?
Системная функция ЦФ определяется отношением Z-преобразования отклика Y(z) и Z-преобразования входного воздействия X(z).
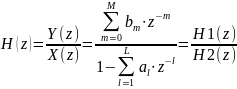
13) На нерекурсивный ЦФ 2 порядка с коэффициентами b0=b1=b2=1 действует сигнал, состоящий из трех временных отсчетов: x(0)=x(1)=x(2)=1. Каково максимальное значение отклика фильтра y(nT)?
3
14) Осуществляет ли нерекурсивный ЦФ 1 порядка полосовую фильтрацию?
Нет.
15) На нерекурсивный ЦФ 2 порядка с коэффициентами b0=b1=b2=1 действует сигнал, состоящий из трех временных отсчетов: x(0)=x(1)=x(2)=1. Сколько ненулевых отсчетов содержит отклик фильтра y(nT)?
y0=1
y1=2
y2=3
y3=2
y4=1
16) Как называется модуль комплексного коэффициента передачи K(jw) ЦФ?
АЧХ.
17) Как называется отклик ЦФ на воздействие в виде единичной функции включения(скачка) 1(nT)?
Переходная функция.
18) Запишите разностное уравнение нерекурсивного ЦФ.

19) Поясните, что такое дискретная свертка сигналов?
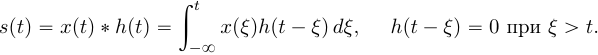 позволяет
рассчитать сигнал
позволяет
рассчитать сигнал
![]() на
выходе линейного фильтра с импульсной
характеристикой
на
выходе линейного фильтра с импульсной
характеристикой
![]() ,
при входном сигнале
,
при входном сигнале
![]() .
При этом предполагается, что
и
—
абсолютно интегрируемые на всей числовой
оси функции, для того чтобы интеграл
сходился.
.
При этом предполагается, что
и
—
абсолютно интегрируемые на всей числовой
оси функции, для того чтобы интеграл
сходился.
20)
Нарисовать структурную схему нерекурсивного
ЦФ 2-го порядка.