- •1. Понятие сау и сар. Функциональные схемы сар
- •2. Классификация автоматических систем
- •– Система стабилизации.
- •3. Описание линейных систем в пространстве переменных состояния
- •4. Построение линейной модели следящей системы
- •5. Определение передаточной функции. Вычисление матричной передаточной функции системы
- •6. Элементы структурных математических моделей систем
- •7. Способ составления смм по дифференциальным уравнениям, представленным в форме Коши
- •Когда задана система уравнений логичней выбрать координаты вектора состояний как переменные, которые входят в состав дифференциальных уравнений.
- •Записываются вектора входа, выхода и состояний.
- •Правила эквивалентных преобразований структурных схем
- •Правила преобразования основных типов соединений динамических элементов
- •14. Понятие переходной и импульсной переходной характеристик и способы нахождения их аналитических выражений
- •15. Понятие типовых динамических звеньев, неминимально-фазовые тдз
- •16. Амплитудная и фазовая частотные характеристики элемента. Их математическая и физическая интерпретация
- •17. Какие преимущества дает использование логарифмических масштабов при построении частотных характеристик по сравнению с линейными масштабами
- •28. Прямой метод исследования устойчивости линейных систем
- •29. Алгебраический критерий устойчивости Гурвица.
- •30. Частотный критерий устойчивости Михайлова. (Принцип аргумента)
- •31. Критерий устойчивости Найквиста для устойчивых разомкнутых систем
- •32. Обобщенный критерий Найквиста
- •33. Понятие запасов устойчивости по фазе и модулю. Исследование устойчивости с помощью лафчх
- •34. Анализ устойчивости многоконтурных систем. Номограмма замыкания
- •35. Метод корневого годографа
- •36. Правила построения траекторий корней в методе корневого годографа
- •37. Определение свободного движения в системе с помощью обратного преобразования Лапласа выражения от ненулевых начальных условий
- •Определение вынужденной составляющей движения в системе
- •38. Основные показатели качества регулирования системы. Их связь с запасами устойчивости
- •39. Приближенная оценка показателей качества по доминирующим полюсам передаточной функции системы
- •40. Анализ и проектирование систем с помощью метода корневого годографа
- •41. Исследование точности регулирования с помощью разложения в степенной ряд передаточной функции ошибки
- •42. Исследование точности регулирования при наличии возмущающего воздействия
- •43. Анализ точности регулирования в статической системе
- •44. Анализ точности регулирования в системах с астатизмом 1-го и 2-го порядка
- •45. Повышение точности методом комбинированного управления
- •47. Построение желаемой логарифмической амплитудной частотной характеристики следящей системы
- •48. Синтез последовательного корректирующего устройства следящей системы
- •49. Назначение корректирующих устройств в сар. Понятие жесткой и гибкой ос
- •50. Понятие управляемости и наблюдаемости. Исследование управляемости и наблюдаемости с помощью приведения системы к диагональному виду.
- •Вопросы к экзамену по курсу “Основы автоматики”
Определение вынужденной составляющей движения в системе
Для любого сигнала:
 ,
где
,
где
 .
Тогда
.
Тогда
 .
.
Найдем свободное
движение в системе:
 .
L
–простые корни, r
– комплексно-сопряженные, k
– кратные. Вычет:
.
L
–простые корни, r
– комплексно-сопряженные, k
– кратные. Вычет:
 .
.
Если все корни
уравнения
 простые и
простые и
 .
Тогда использую теорему разложения
получим:
.
Тогда использую теорему разложения
получим:

Если имеются кратные корни, то
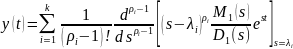
Если имеются комплексно-сопряженные корни, то

Обобщая все сказанное получаем общую формулу:
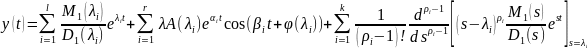

38. Основные показатели качества регулирования системы. Их связь с запасами устойчивости
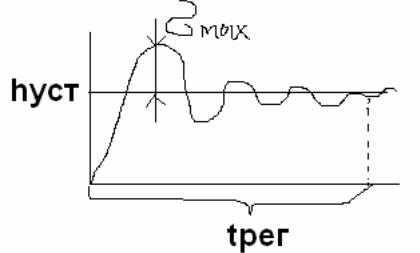
Показателями качества являются:
Время регулирования
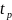 – время, за которое выходной сигнал
перестанет отклоняться более чем на
5% от установившегося значения.
– время, за которое выходной сигнал
перестанет отклоняться более чем на
5% от установившегося значения.Максимальное перерегулирование:
 .
.Число N колебаний за время регулирования.
Собственная частота колебаний
 .
.Логарифмический декремент затухания.
Максимальная скорость.
Возможны следующие
типы переходных процессов: колебательный,
монотонный (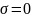 ,
присутсвуют колебания)
и апериодический (
,
отсутствуют колебания).
,
присутсвуют колебания)
и апериодический (
,
отсутствуют колебания).
Для частной задачи может быть введена аналитическая зависимость, связывающая характер переходного процесса и запасов устойчивости:
Апериодический:
 .
.Монотонный:
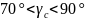 .
.Колебательный:

39. Приближенная оценка показателей качества по доминирующим полюсам передаточной функции системы
Пусть доминирующими
полюсами являются
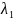 и
и
 ,
причем
,
причем
 .
Тогда на координатной плоскости
отмечаются эти полюса, а также полюса
(крестиками) и нули (ноликами) данной
функции.
.
Тогда на координатной плоскости
отмечаются эти полюса, а также полюса
(крестиками) и нули (ноликами) данной
функции.
Время регулирования оценивается следующим образом:
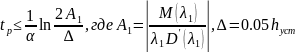
Если
 ,
то используют следующую формулу:
,
то используют следующую формулу:

Максимальное перерегулирования оценивается по формуле:

Здесь
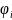 – углы векторов, проведенные из полюсов
системы (комплексно-сопряженная точка
и точка покоя уже учтены в формуле) к
,
– углы векторов, проведенные из полюсов
системы (комплексно-сопряженная точка
и точка покоя уже учтены в формуле) к
,
 – углы векторов, проведенные из нулей
к
.
– углы векторов, проведенные из нулей
к
.
При расположении
полюсов под углом
 скорость установления системы будет
максимальной, т.е. время регулирования
будет минимальным.
скорость установления системы будет
максимальной, т.е. время регулирования
будет минимальным.
 Наибольшее
влияние на переходный процесс оказывают
полюса, находящиеся ближе к мнимой оси.
Удаленные полюса мало влияют на переходный
процесс, а на качество вообще не влияют
можно
пренебрегать этими составляющими
движения.
Наибольшее
влияние на переходный процесс оказывают
полюса, находящиеся ближе к мнимой оси.
Удаленные полюса мало влияют на переходный
процесс, а на качество вообще не влияют
можно
пренебрегать этими составляющими
движения.
Вычеты в ближних полюсах больше - полюса доминируют (доминировать могут как действительные, так и комплексные полюса).
40. Анализ и проектирование систем с помощью метода корневого годографа

В данной системе истинный коэффициент
усиления
 ,
кроме того система имеет два полюса:
,
кроме того система имеет два полюса:
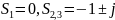 .
.
Согласно правилам построения траекторий корней годографа:
Имеется три ветви корневого годографа, картина будет симметричной, траектории непрерывные.
Ветви начинаются в полюсах.
При
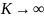 :
:
 .
.При
 :
:
 ,
,
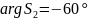 ,
при
,
при
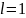 :
:
 .
.Точка пересечения:
 .
.
Полюс находится на действительной оси, значит корень в нуле движется к
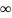 .
.Углы выхода корневого годографа из мнимых полюсов:
 .
.Пересечений с действительной осью нет.
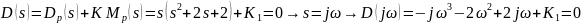 :
:

Откуда получаем корни:
 .
.
При
 Система будет неустойчивой. При
Система будет неустойчивой. При
 третий корень на вещественной оси будет
находиться в точке
третий корень на вещественной оси будет
находиться в точке
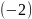 .
.