- •1. Понятие сау и сар. Функциональные схемы сар
- •2. Классификация автоматических систем
- •– Система стабилизации.
- •3. Описание линейных систем в пространстве переменных состояния
- •4. Построение линейной модели следящей системы
- •5. Определение передаточной функции. Вычисление матричной передаточной функции системы
- •6. Элементы структурных математических моделей систем
- •7. Способ составления смм по дифференциальным уравнениям, представленным в форме Коши
- •Когда задана система уравнений логичней выбрать координаты вектора состояний как переменные, которые входят в состав дифференциальных уравнений.
- •Записываются вектора входа, выхода и состояний.
- •Правила эквивалентных преобразований структурных схем
- •Правила преобразования основных типов соединений динамических элементов
- •14. Понятие переходной и импульсной переходной характеристик и способы нахождения их аналитических выражений
- •15. Понятие типовых динамических звеньев, неминимально-фазовые тдз
- •16. Амплитудная и фазовая частотные характеристики элемента. Их математическая и физическая интерпретация
- •17. Какие преимущества дает использование логарифмических масштабов при построении частотных характеристик по сравнению с линейными масштабами
- •28. Прямой метод исследования устойчивости линейных систем
- •29. Алгебраический критерий устойчивости Гурвица.
- •30. Частотный критерий устойчивости Михайлова. (Принцип аргумента)
- •31. Критерий устойчивости Найквиста для устойчивых разомкнутых систем
- •32. Обобщенный критерий Найквиста
- •33. Понятие запасов устойчивости по фазе и модулю. Исследование устойчивости с помощью лафчх
- •34. Анализ устойчивости многоконтурных систем. Номограмма замыкания
- •35. Метод корневого годографа
- •36. Правила построения траекторий корней в методе корневого годографа
- •37. Определение свободного движения в системе с помощью обратного преобразования Лапласа выражения от ненулевых начальных условий
- •Определение вынужденной составляющей движения в системе
- •38. Основные показатели качества регулирования системы. Их связь с запасами устойчивости
- •39. Приближенная оценка показателей качества по доминирующим полюсам передаточной функции системы
- •40. Анализ и проектирование систем с помощью метода корневого годографа
- •41. Исследование точности регулирования с помощью разложения в степенной ряд передаточной функции ошибки
- •42. Исследование точности регулирования при наличии возмущающего воздействия
- •43. Анализ точности регулирования в статической системе
- •44. Анализ точности регулирования в системах с астатизмом 1-го и 2-го порядка
- •45. Повышение точности методом комбинированного управления
- •47. Построение желаемой логарифмической амплитудной частотной характеристики следящей системы
- •48. Синтез последовательного корректирующего устройства следящей системы
- •49. Назначение корректирующих устройств в сар. Понятие жесткой и гибкой ос
- •50. Понятие управляемости и наблюдаемости. Исследование управляемости и наблюдаемости с помощью приведения системы к диагональному виду.
- •Вопросы к экзамену по курсу “Основы автоматики”
35. Метод корневого годографа

Пусть имеется
разомкнутая система:
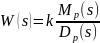 ,
где
,
где
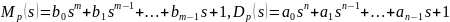 .
Здесь
.
Здесь
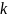 – истинный коэффициент усиления
разомкнутой системы. Тогда запишем:
– истинный коэффициент усиления
разомкнутой системы. Тогда запишем:
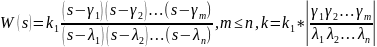
Для замкнутой
системы:
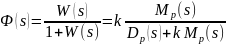 .
.
Нули разомкнутой системы остаются нулями замкнутой системы, а полюса замкнутой системы изменяются.
Метод корневого
годографа заключается в отыскании
корней
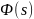 :
:
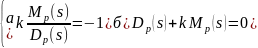
Корневой годограф
– это траектории корней характеристического
уравнения замкнутой системы, полученные
при изменении
разомкнутой системы (передаточной
функции) от
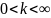 на комплексной плоскости S.
на комплексной плоскости S.
Уравнение (а) распадается на уравнение для модулей и уравнение для аргументов:

Пусть траектория
проходит через исследуемую точку, тогда:
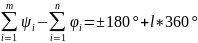 ,
где
,
где
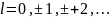 - не длина векторов.
- не длина векторов.
Если выполняется
уравнение (а), то через исследуемую точку
обязательно пройдет одна из ветвей
корневого годографа. Чтобы определить
при каком
это будет выполняться составляют
уравнения для модулей по уравнению (а):
 .
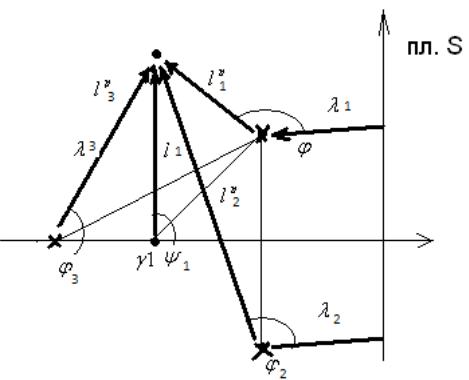
И находят
.
И находят
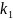 из которого пересчитывается истинный
коэффициент.
из которого пересчитывается истинный
коэффициент.
 Для
устойчивости системы достаточно, чтобы
корни располагались слева.
Для
устойчивости системы достаточно, чтобы
корни располагались слева.
36. Правила построения траекторий корней в методе корневого годографа
Количество годографов равно порядку
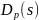 .
Каждая ветвь корневого годографа
является непрерывной кривой, зависящей
от K.
Комплексные части годографов всегда
сопряженные (можно рассматривать только
половину полуплоскости).
.
Каждая ветвь корневого годографа
является непрерывной кривой, зависящей
от K.
Комплексные части годографов всегда
сопряженные (можно рассматривать только
половину полуплоскости).Поведение корневого годографа при
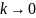 .
Из уравнения
.
Из уравнения
 видно, что ветви корневого годографа
начинаются в полюсах разомкнутой
системы.
видно, что ветви корневого годографа
начинаются в полюсах разомкнутой
системы.Поведение корневого годографа при
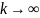 .
.
Если
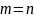 ,
то
,
то
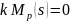 ,
значит ветви корневого годографа
заканчиваются в нулях передаточной
функции.
,
значит ветви корневого годографа
заканчиваются в нулях передаточной
функции.
Если
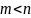 ,
то рассматривается его поведение на
,
то рассматривается его поведение на
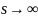 :
:
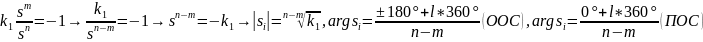 ,
т.е.
,
т.е.
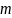 штук ветвей корневого годографа
заканчиваются в нулях передаточной
функции и разомкнутой системы, а
остальные
штук ветвей корневого годографа
заканчиваются в нулях передаточной
функции и разомкнутой системы, а
остальные
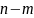 уходят на бесконечность вдоль асимптот
в виде прямых, расположенных под углами
уходят на бесконечность вдоль асимптот
в виде прямых, расположенных под углами
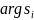 .
.Уточнение точки пересечения асимптот.
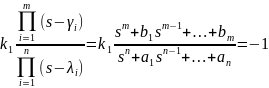 .
В результате деления полинома получаем:
.
В результате деления полинома получаем:
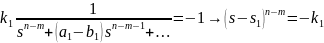 ,
где
,
где
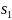 – точка пересечения асимптот по формуле
бинома Ньютона. При
получаем:
– точка пересечения асимптот по формуле
бинома Ньютона. При
получаем:
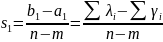 .
.
Корневой годограф на вещественной оси определяется с помощью уравнения для аргумента:
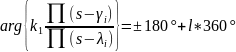
Определение углов выхода ветвей корневого годографа из комплексно-сопряженных полюсов (
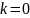 ).
Из действительной может двигаться либо
к 0, либо к 180, т.е. движение по действительной
оси. Для системы третьего порядка угол
выхода определяется по формуле:
).
Из действительной может двигаться либо
к 0, либо к 180, т.е. движение по действительной
оси. Для системы третьего порядка угол
выхода определяется по формуле:
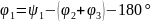 .
.Точки пересечения ветвей годографа с действительной осью. Либо приходят, либо уходят.
Точки пересечения ветвей годографа с мнимой осью. Записываем уравнение
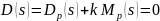 ,
подставляем
,
подставляем
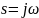 и из полученной системы двух уравнений:
и из полученной системы двух уравнений:
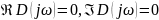 находим точку пересечения мнимой оси
(
находим точку пересечения мнимой оси
(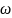 )
и угол (
).
)
и угол (
).Если все звенья в разомкнутой системе положительные и не выше второго порядка, то в результате замыкания единичной ООС система никогда не станет неустойчивой.
37. Определение свободного движения в системе с помощью обратного преобразования Лапласа выражения от ненулевых начальных условий
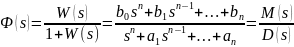

Пусть имеется n произвольных начальных условий:
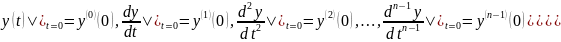
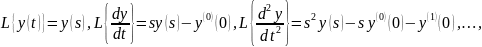
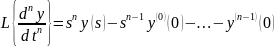
Применим преобразования Лапласа к
выражению (*):
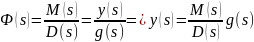 – при ненулевых начальных условиях.
Окончательно получаем:
– при ненулевых начальных условиях.
Окончательно получаем:
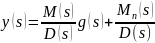 ,
где
,
где
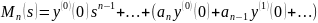 .
Тогда
.
Тогда
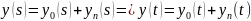 .
.
Найдем свободное движение в системе:
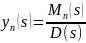 .
Порядок числителя меньше порядка
знаменателя (если они равны, то свободное
движение невозможно). При разбиении на
дроби целая часть не отображается. L
–простые корни, r –
комплексно-сопряженные, k
– кратные.
.
Порядок числителя меньше порядка
знаменателя (если они равны, то свободное
движение невозможно). При разбиении на
дроби целая часть не отображается. L
–простые корни, r –
комплексно-сопряженные, k
– кратные.
Вычет:
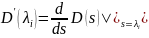 .
.