32. Обобщенный критерий Найквиста

Пусть – количество корней характеристического уравнения разомкнутой системы в правой полуплоскости, а – количество характеристических уравнений замкнутой системы в правой полуплоскости.

Перейдем к частотам : . Где – количество оборотов годографа относительно «-1».

Формулировка критерия:

1. Если разомкнутая система устойчива ( ), то для устойчивости замкнутой системы ( ) годограф не должен охватывать «-1».

2. Пусть разомкнутая система неустойчива и имеет коней, то для устойчивости замкнутой системы ( ) количество оборотов должно быть равно для полного диапазона и для половинного диапазона.

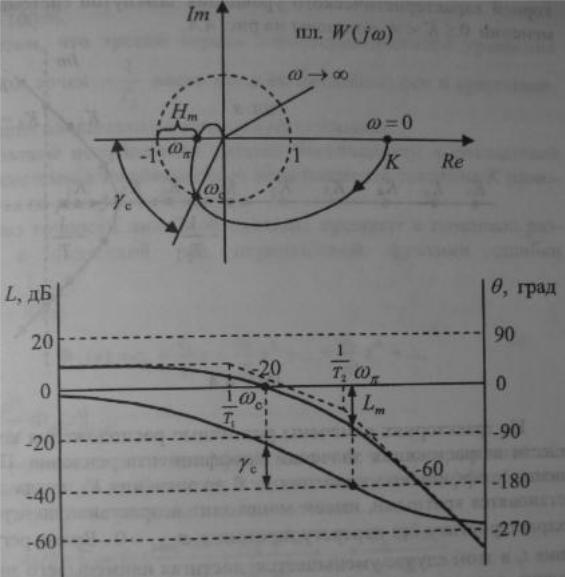
33. Понятие запасов устойчивости по фазе и модулю. Исследование устойчивости с помощью лафчх

В условии эксплуатации параметры системы по тем или иным причинам могут меняться в определенных пределах. Эти колебания параметров могу привести к потере устойчивости системы, если она работает вблизи границы устойчивости. Поэтому стремятся спроектировать САУ так, чтобы она работала вдали от границы устойчивости, степень этого удаления называют запасом устойчивости. По годографу и соответствующим ЛАФЧХ разомкнутой системы вводится количественная мера устойчивости в виде запасов устойчивости по фазе и модулю.

Запас по фазе определяют на частоте среза системы, т.е. когда амплитуды входного и выходного сигналов равны. Запас по фазе показывает, какой дополнительный отрицательный фазовый сдвиг допустим в системе прежде, чем она окажется на границе устойчивости.

Запас по модулю определяется на частоте , где фазовая характеристика равна .Запас по модулю показывает во сколько раз может быть увеличен коэффициент усиления системы, прежде чем она окажется на границе неустойчивости.

Логорифмический запас устойчивости: .

При увеличении K ЛАФЧХ смещается вверх на значение , годограф раздувается, частота среза увеличивается, а запас фазы уменьшается.

Из практики были получены следующие значения нормативных запасов устойчивости запасов устойчивости в зависимости от :

34. Анализ устойчивости многоконтурных систем. Номограмма замыкания

Исследование с помощью критерия Найквиста начинаем с внутреннего контура. Размыкаем его по сигналу обратной связи. . Если , то система устойчива, а если , то система неустойчива. Далее строится ЛАФЧХ, а по нему годограф. Смотрят, сколько раз он охватывает точку «-1» и делают вывод об устойчивости. Если оказывается, что система неустойчива, то определяют количество корней в правой полуплоскости.

Переходят к исследованию внешнего контура. Размыкают: . Для построения характеристики , т.е. исследования замкнутой системы рассматриваем:

Подставляя в получаем связь:

Для решения задачи построения ЛАФЧХ замкнутой системы по ЛАФЧХ разомкнутой системы используется номограмма Никольса. и являются функциями двух переменных и представляют собой поверхность. В области высших частот замкнутая система ведет себя как разомкнутая , значит амплитудная и фазовая характеристики будут совпадать.