28. Прямой метод исследования устойчивости линейных систем

Пусть задана линеаризованная автономная система: , то его решение , а положение равновесия одно и тоже: . Ищут решения в виде: , используя условие: , при этом задают заранее.

1. Условие асимптотической устойчивости: ,т.е. все корни характеристического уравнения лежат в левой полуплоскости. Если линейная система асимптотически устойчива, то и исходная нелинейная система асимптотически устойчива.

2. Как только найдется хотя бы одно , линеаризованная модель неустойчива, переходная характеристика уходит на бесконечность, исходная нелинейная модель неустойчива.

3. Если из всех , обнаруживается λ лежащее на мнимой оси, то возникает неопределенность.

4. Если имеется звено , то получаем устойчивое положение равновесия, а – неустойчива.

Задача: При исследовании систем на устойчивость ориентироваться на корни характеристического уравнения. Прямой метод исследования устойчивости линейных систем сводится к анализу расположения и поиска на комплексной плоскости.

29. Алгебраический критерий устойчивости Гурвица.

Строится матрица . Первая строка – нечетные индексы, вторая строка – четные индексы, последующие строки – смещение блока вправо на один столбец, причем пропуски заполняются нулями, до тех пор, пока не заполнится n-ая строка.

Необходимое условие асимптотической устойчивости: Все коэффициенты являются положительными, т.е. .

Достаточное условие устойчивости (Матрица Гурвица): Все угловые миноры являются положительными.

30. Частотный критерий устойчивости Михайлова. (Принцип аргумента)

Пусть корни характеристического уравнения : Тогда . Рассмотрим данное выражение как произведение векторов на комплексной плоскости:

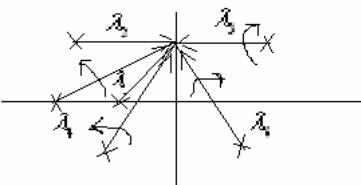
Здесь n – число всех корней, а m – число корней в правой полуплоскости. – функция четных степеней (четная функция), – функция нечетных степеней (нечетная функция).

Значит можно отбросить отрицательный диапазон частот и перейти к физическим:

Для установившейся системы: :

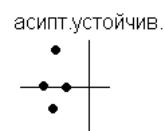
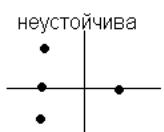
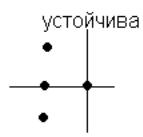
Формулировка критерия. Для того, чтобы линейная система была асимптотически устойчива, необходимо и достаточно, чтобы годограф характеристического уравнения начинался на положительной части действительной оси, проходил последовательно n квадрантов в положительном направлении, не попадая в начало координат.

31. Критерий устойчивости Найквиста для устойчивых разомкнутых систем

Позволяет исследовать устойчивость замкнутой системы по частотным характеристикам разомкнутой. Основан на критерии Михайлова. Рассмотрим передаточную функцию разомкнутой системы: . Нули замкнутой системы сохраняются: . Тогда характеристическое уравнение замкнутой системы: . Вспомогательная функция: .

Применяя к функции критерий Михайлова:

Формулировка. Если разомкнутая система является устойчивой, то для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф разомкнутой системы не охватывал «-1» при изменении частоты .

Формулировка. Если разомкнутая система является неустойчивой, то замкнутая система будет устойчивой, если годограф охватывает «-1» в положительном направлении раз при .