
- •1. Понятие сау и сар. Функциональные схемы сар
- •2. Классификация автоматических систем
- •– Система стабилизации.
- •3. Описание линейных систем в пространстве переменных состояния
- •4. Построение линейной модели следящей системы
- •5. Определение передаточной функции. Вычисление матричной передаточной функции системы
- •6. Элементы структурных математических моделей систем
- •7. Способ составления смм по дифференциальным уравнениям, представленным в форме Коши
- •Когда задана система уравнений логичней выбрать координаты вектора состояний как переменные, которые входят в состав дифференциальных уравнений.
- •Записываются вектора входа, выхода и состояний.
- •Правила эквивалентных преобразований структурных схем
- •Правила преобразования основных типов соединений динамических элементов
- •14. Понятие переходной и импульсной переходной характеристик и способы нахождения их аналитических выражений
- •15. Понятие типовых динамических звеньев, неминимально-фазовые тдз
- •16. Амплитудная и фазовая частотные характеристики элемента. Их математическая и физическая интерпретация
- •17. Какие преимущества дает использование логарифмических масштабов при построении частотных характеристик по сравнению с линейными масштабами
- •28. Прямой метод исследования устойчивости линейных систем
- •29. Алгебраический критерий устойчивости Гурвица.
- •30. Частотный критерий устойчивости Михайлова. (Принцип аргумента)
- •31. Критерий устойчивости Найквиста для устойчивых разомкнутых систем
- •32. Обобщенный критерий Найквиста
- •33. Понятие запасов устойчивости по фазе и модулю. Исследование устойчивости с помощью лафчх
- •34. Анализ устойчивости многоконтурных систем. Номограмма замыкания
- •35. Метод корневого годографа
- •36. Правила построения траекторий корней в методе корневого годографа
- •37. Определение свободного движения в системе с помощью обратного преобразования Лапласа выражения от ненулевых начальных условий
- •Определение вынужденной составляющей движения в системе
- •38. Основные показатели качества регулирования системы. Их связь с запасами устойчивости
- •39. Приближенная оценка показателей качества по доминирующим полюсам передаточной функции системы
- •40. Анализ и проектирование систем с помощью метода корневого годографа
- •41. Исследование точности регулирования с помощью разложения в степенной ряд передаточной функции ошибки
- •42. Исследование точности регулирования при наличии возмущающего воздействия
- •43. Анализ точности регулирования в статической системе
- •44. Анализ точности регулирования в системах с астатизмом 1-го и 2-го порядка
- •45. Повышение точности методом комбинированного управления
- •47. Построение желаемой логарифмической амплитудной частотной характеристики следящей системы
- •48. Синтез последовательного корректирующего устройства следящей системы
- •49. Назначение корректирующих устройств в сар. Понятие жесткой и гибкой ос
- •50. Понятие управляемости и наблюдаемости. Исследование управляемости и наблюдаемости с помощью приведения системы к диагональному виду.
- •Вопросы к экзамену по курсу “Основы автоматики”
14. Понятие переходной и импульсной переходной характеристик и способы нахождения их аналитических выражений
Переходная характеристика – реакция системы на единичное ступенчатое входное воздействие, представленная как функция времени.

 – переходная
характеристика.
– переходная
характеристика.
Импульсная
характеристика – реакция системы на
абстрактный импульс:
 .
.


Гармоническое входное воздействие:
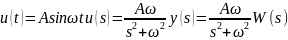
Кроме того выходной сигнал можно вычислять как интеграл свертки:
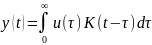
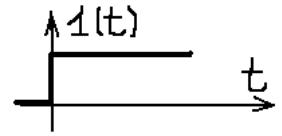
15. Понятие типовых динамических звеньев, неминимально-фазовые тдз
Динамическое звено — математическая модель элемента или его части, записанная в виде дифференциального уравнения или передаточной функции.
Динамические звенья, которые описываются дифференциальными уравнениями не выше 2-го порядка, принято называть типовыми динамическими звеньями. Передаточная функция называется минимально-фазовой, если все её нули расположены в левой половине S плоскости.
Типовые динамические звенья:
Апериодическое устойчивое звено:

Апериодическое неустойчивое звено:
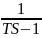
Интегрирующее звено:

Колебательное устойчивое звено:

Колебательное неустойчивое звено:

Вырожденное колебательное звено:
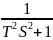
Минимально-фазовое дифференциальное звено первого порядка:
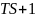
Неминимально-фазовое дифференциальное звено первого порядка:
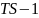
Идеальное дифференциальное звено первого порядка:

Минимально-фазовое дифференциальное звено второго порядка:
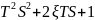
Неминимально-фазовое дифференциальное звено II-го порядка:

Вырожденное дифференциальное звено второго порядка (пробка):

Звено запаздывания:
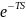
16. Амплитудная и фазовая частотные характеристики элемента. Их математическая и физическая интерпретация
Частотной
характеристикой ТДЗ называют функцию
комплексного аргумента jω
полученную путём формальной замены
 .
Тем самым переходят к частотным
характеристикам (от преобразований
Лапласа к Фурье). Преобразование Фурье
показывает, как распределена по частотам
характеристика системы.
.
Тем самым переходят к частотным
характеристикам (от преобразований
Лапласа к Фурье). Преобразование Фурье
показывает, как распределена по частотам
характеристика системы.
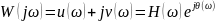
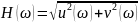

Частотные
характеристики исследуются при подаче
гармонического входного воздействия
 ,
при этом в установившемся режиме:
,
при этом в установившемся режиме:
 .
Т.е. на выходе устанавливается гармоническое
колебание с той же частотой, а если
колебания будут не гармоническими, то
мы имеем дело с нелинейным элементом.
.
Т.е. на выходе устанавливается гармоническое
колебание с той же частотой, а если
колебания будут не гармоническими, то
мы имеем дело с нелинейным элементом.
Если начать изменять
частоту, то заметим, что
 .
Изменяя
.
Изменяя
 устанавливается область линейности, а
изменяя частоту находят вырождение
передаточной функции.
устанавливается область линейности, а
изменяя частоту находят вырождение
передаточной функции.

17. Какие преимущества дает использование логарифмических масштабов при построении частотных характеристик по сравнению с линейными масштабами
График ЛАЧХ произведения ТДЗ является суммой ЛАЧХ каждого из них, таким образом, получение ЛАЧХ системы ТДЗ существенно упрощается.
Асимптотические ЛАЧХ являются прямыми линиями, а не экспонентами, это упрощает их получение и отображение на соответствующих плоскостях.
Асимптотические ЛАЧХ имеют фиксированный наклон, кратный 20 дБ (40 дБ, 60 дБ и т.д.) на декаду, что эквивалентно 6 дБ/октаву (иногда удобнее использовать) (декада — изменение частоты в 10 раз, октава — в 2 раза).
Изменения происходят в пределах декады (+- 10 раз) от характерной точки (
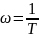 ),
а для более сложных систем в +10 раз от
максимальной характерной точки и в –10
раз от минимальной характерной точки.
),
а для более сложных систем в +10 раз от
максимальной характерной точки и в –10
раз от минимальной характерной точки.ЛФЧХ, чаще всего, является симметрична или кососимметрична относительно сопрягающей частоты (для типовых звеньев).
ЛФЧХ сложной системы является суммой ФЧХ ТДЗ.
Большое количество номограмм, шаблонов и приближённых формул составлены именно для систем изображенных в логарифмическом масштабе.
ЛАФЧХ дифференциального звена – это перевернутая ЛАФЧХ соответствующего интегрального звена, т.е. число соответствующих ЛАФЧХ для исследуемых ТДЗ уменьшается почти в два раза.
Если
 – АЧХ в линейном масштабе, то в
логарифмическом масштабе это
представляется следующим образом:
– АЧХ в линейном масштабе, то в
логарифмическом масштабе это
представляется следующим образом:
 ,
таким образом, если в линейном масштабе
график построен на интервале
,
таким образом, если в линейном масштабе
график построен на интервале
 ,
то в логарифмическом масштабе это
выглядит так:
,
то в логарифмическом масштабе это
выглядит так:
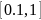 .
.
18. Годограф и логарифмические амплитудные и фазовые частотные характеристики апериодического устойчивого и неустойчивого звена









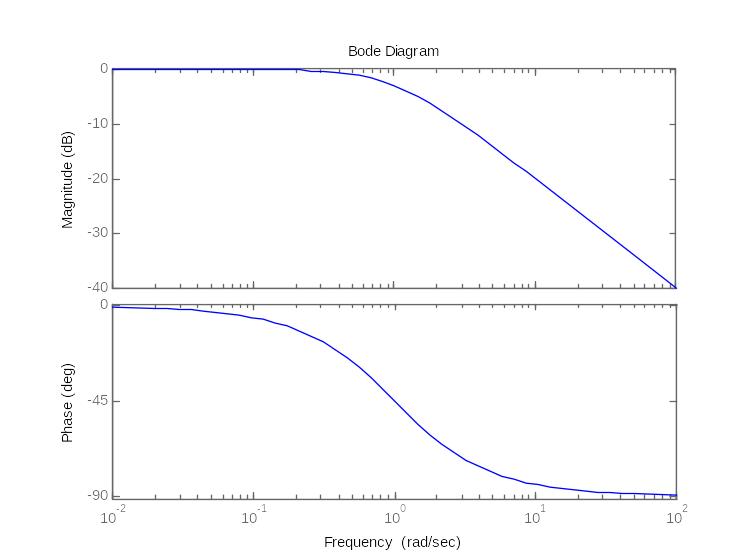
апериодического неустойчивого звена
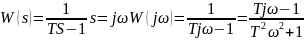
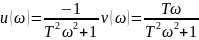
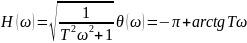
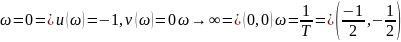
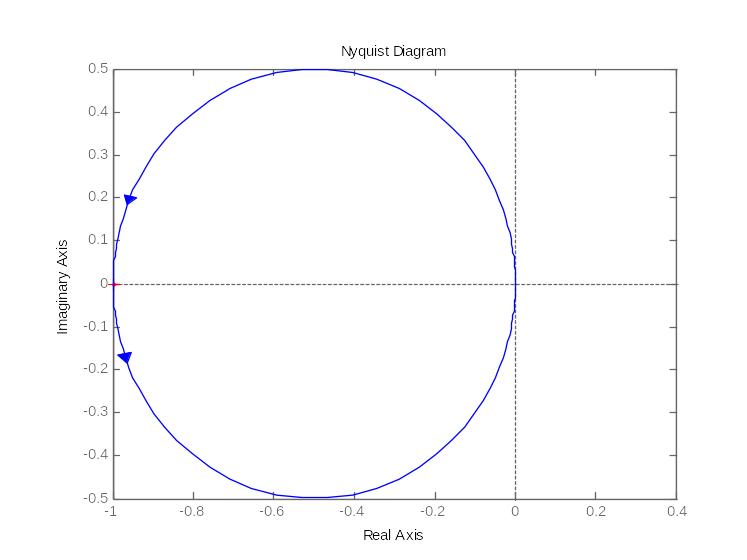
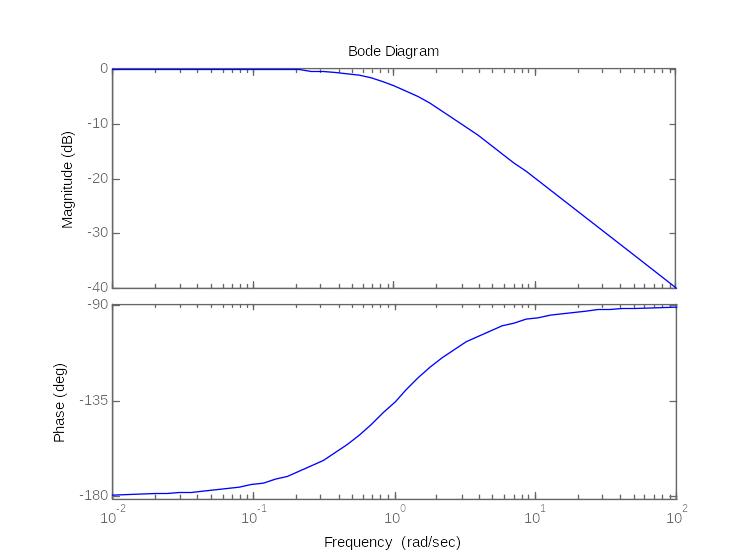
19. Годограф и логарифмические амплитудные и фазовые частотные характеристики интегрирующего и идеально дифференцирующего звена
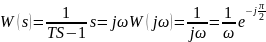




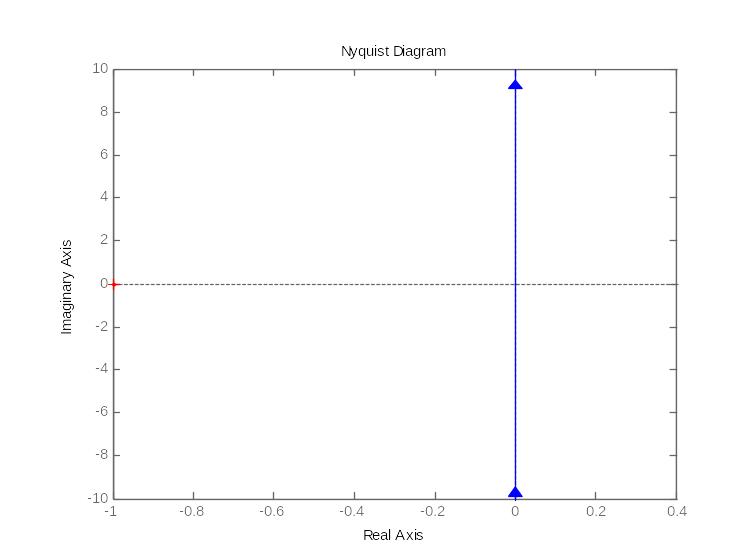
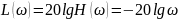
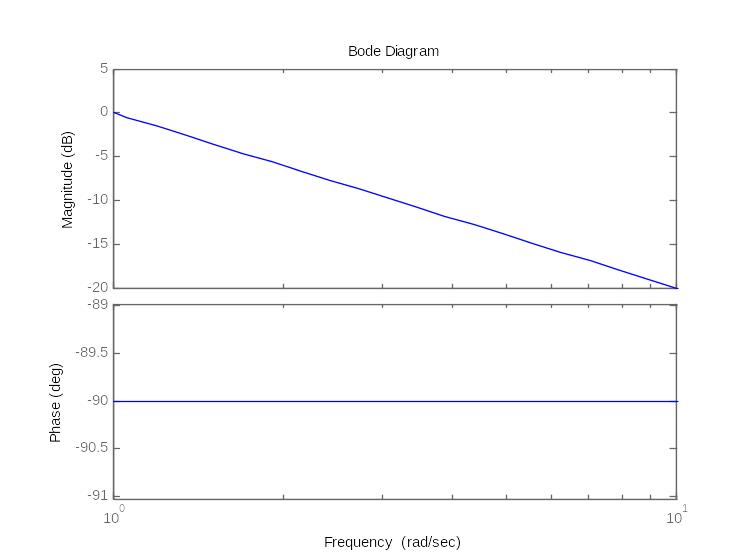
идеального дифференцирующего звена 1-го порядка
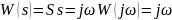


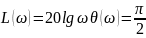


20. Годограф и логарифмические амплитудные и фазовые частотные характеристики колебательного устойчивого звена
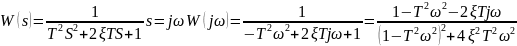

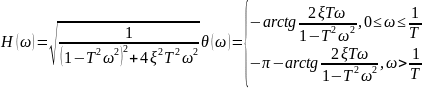
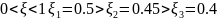
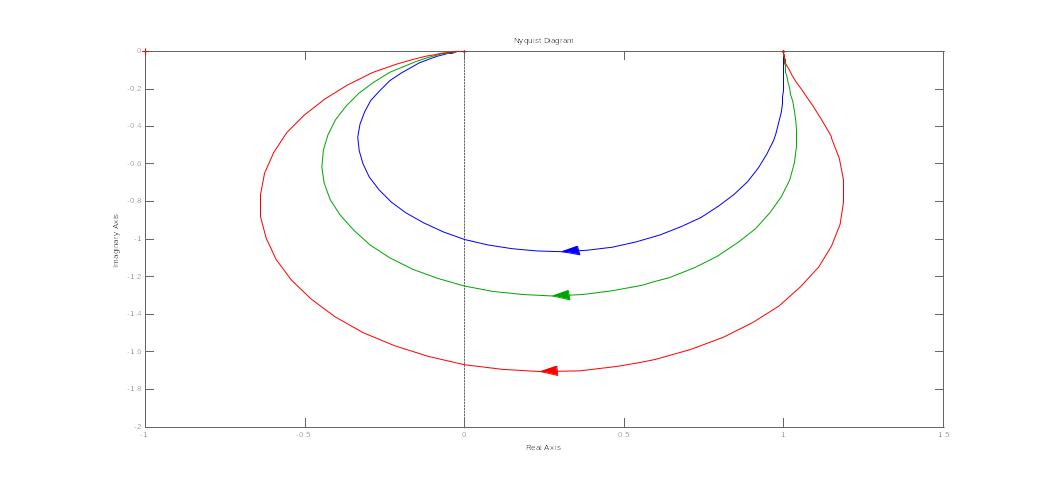


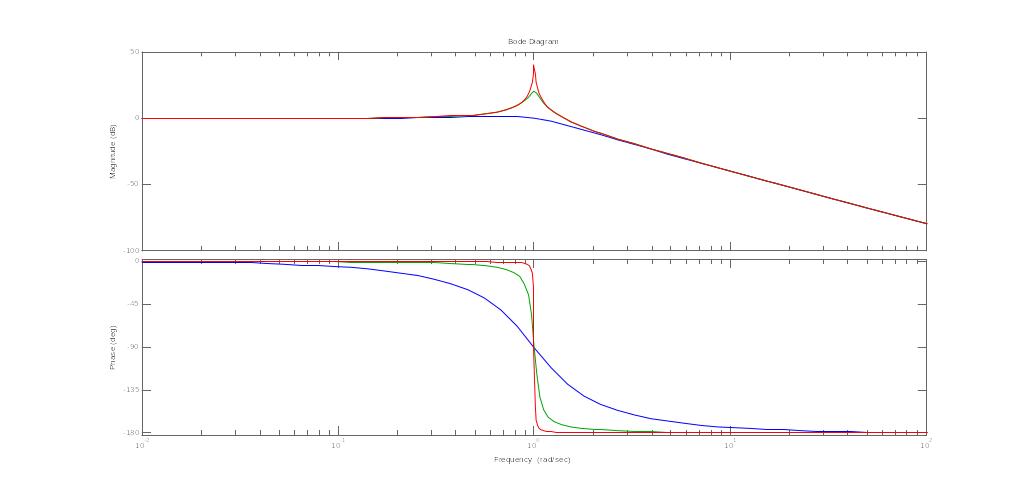
колебательного неустойчивого звена



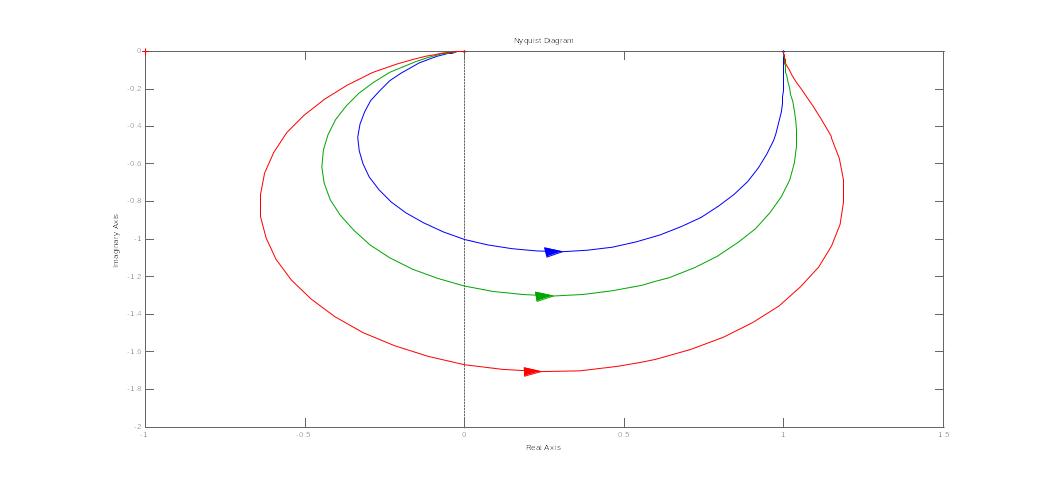
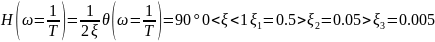
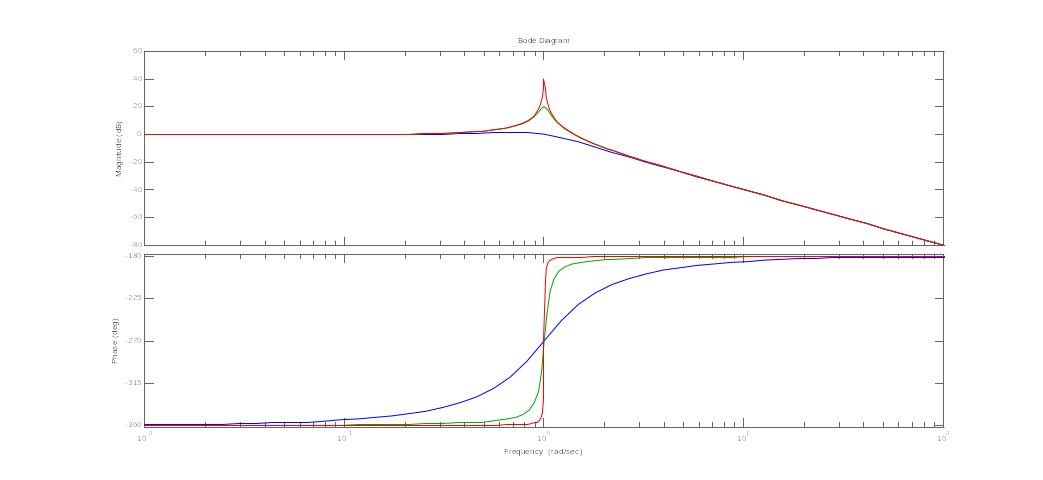
21. Годограф и логарифмические амплитудные и фазовые частотные характеристики вырожденного колебательного звена
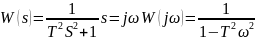
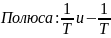
Обходя справа полюса слева примем консервативное звена за устойчивое. Фаза имеет разрыв либо в нуле, либо в 180. Т.к. считаем, что звено устойчивое, то будет скачок на 180 по дуге бесконечно большого радиуса.
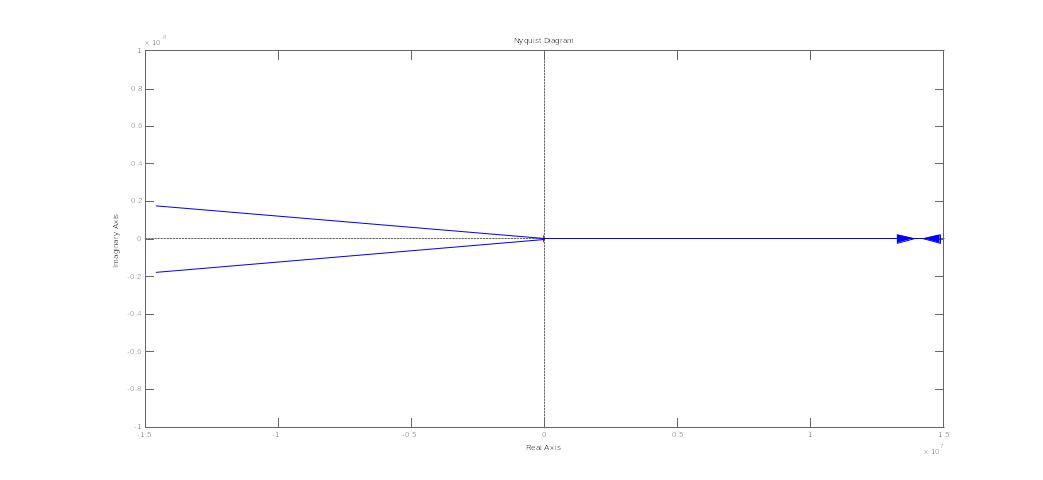
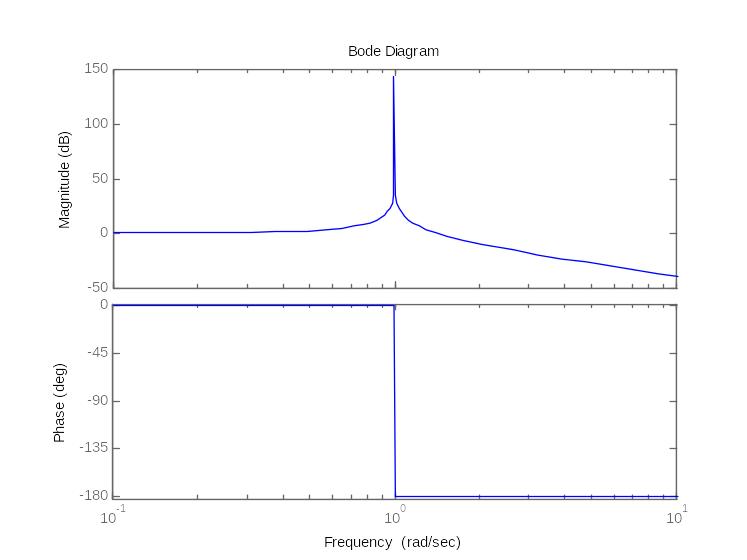
22. Годограф и логарифмические амплитудные и фазовые частотные характеристики минимально-фазового дифференцирующего звена 1-го порядка
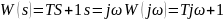

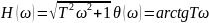

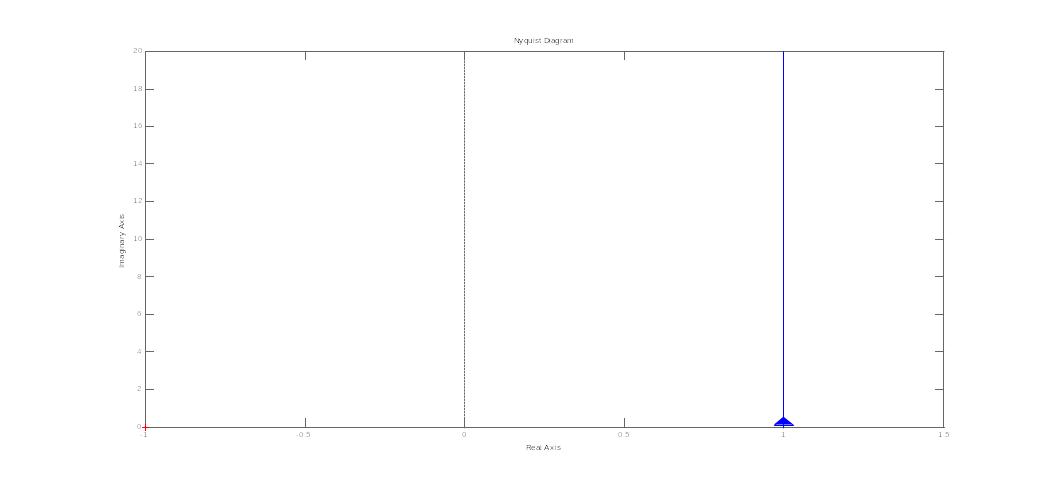

неминимально-фазового дифференцирующего звена 1-го порядка




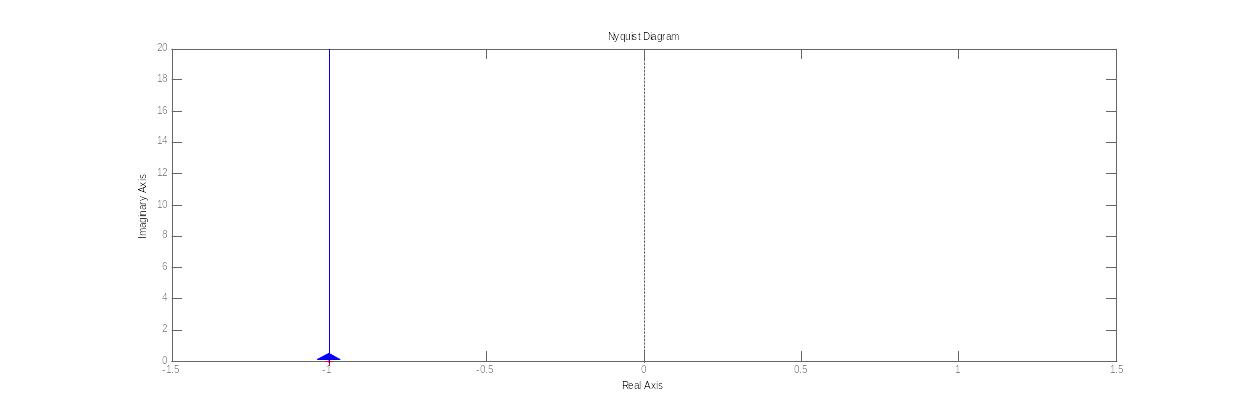
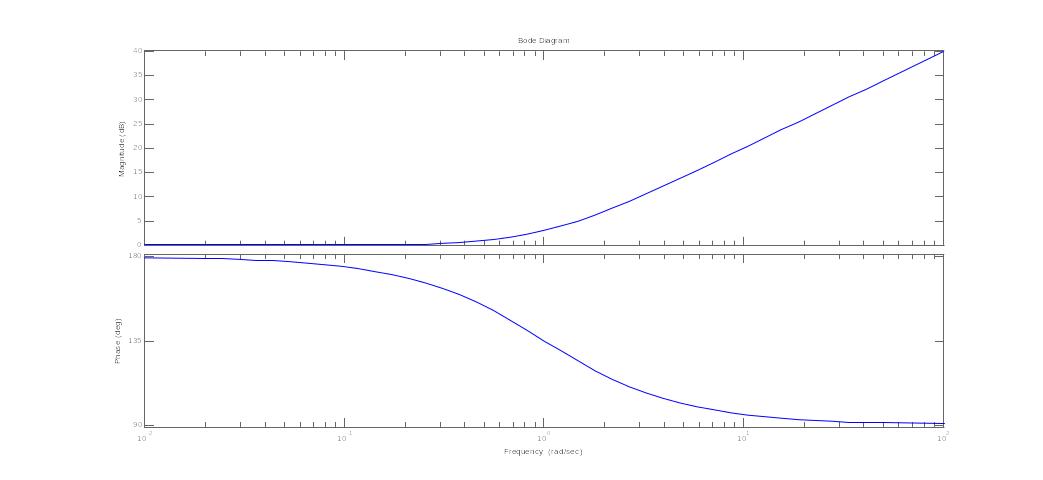
23. Годограф и логарифмические амплитудные и фазовые частотные характеристики минимально-фазового дифференцирующего звена 2-го порядка

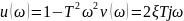
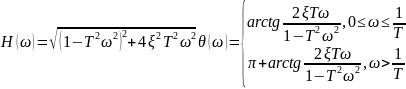

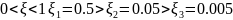

характеристики неминимально-фазового дифференцирующего звена 2-го порядка
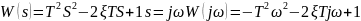
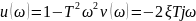
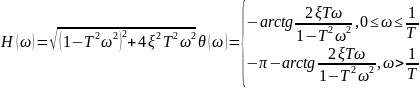
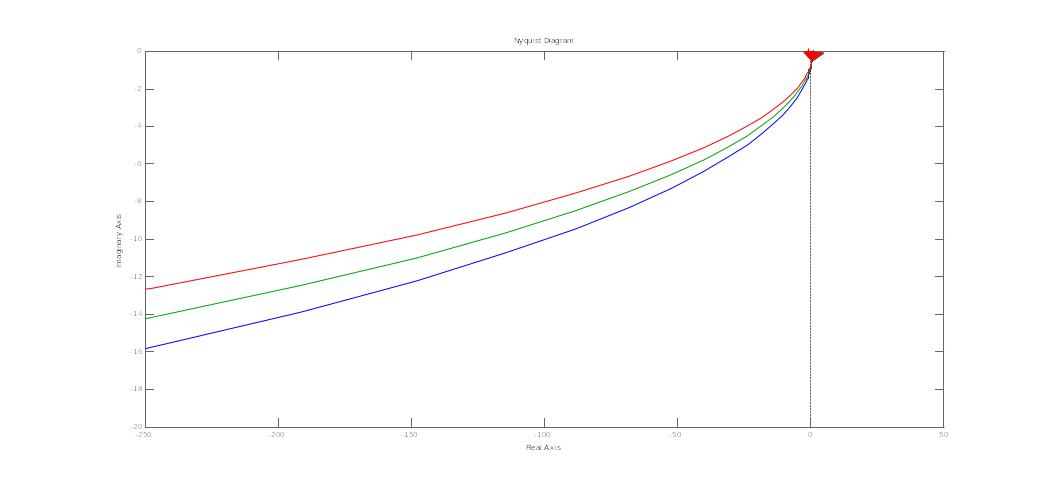
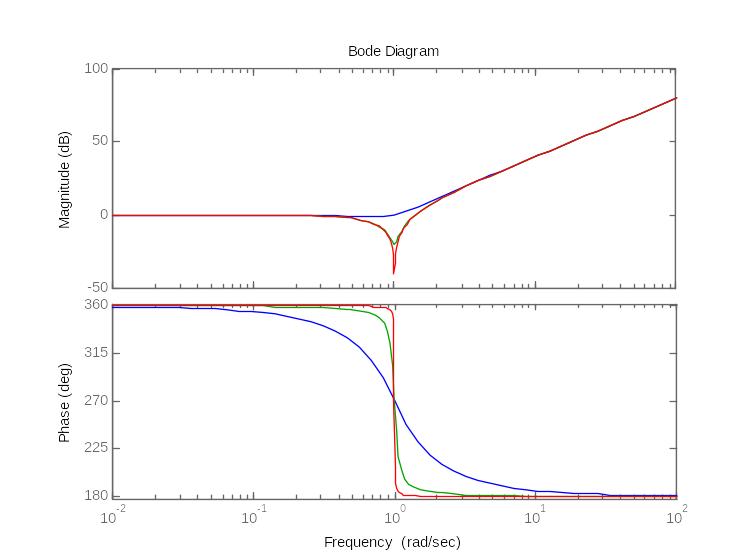
24. Годограф и логарифмические амплитудные и фазовые частотные характеристики вырожденного дифференцирующего звена 2-го порядка

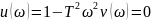
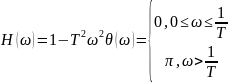
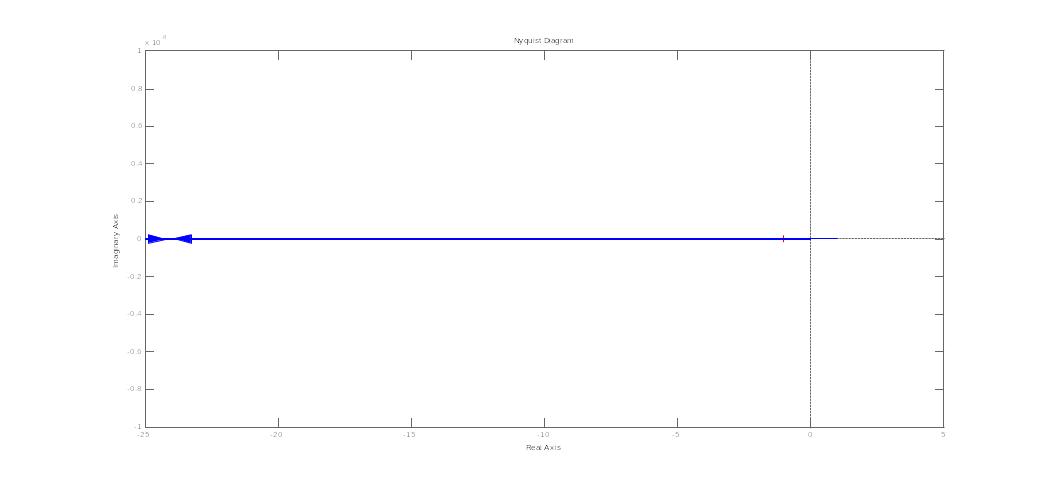
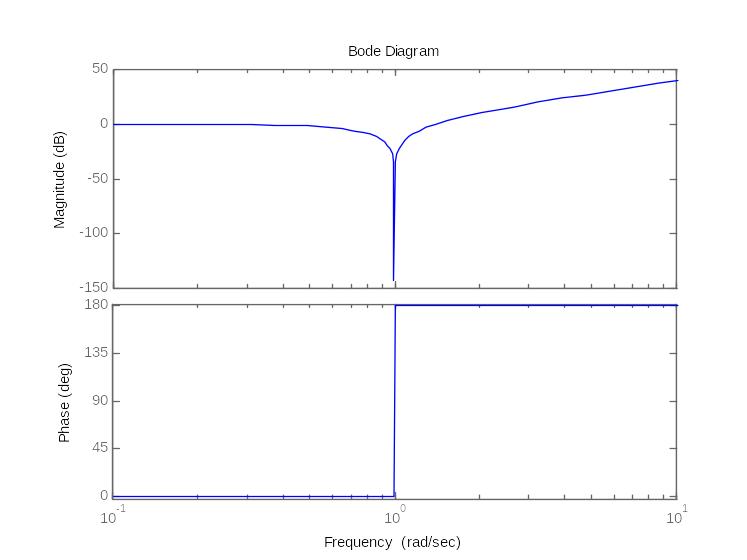
25. Годограф и логарифмические амплитудные и фазовые частотные характеристики звена запаздывания
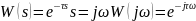


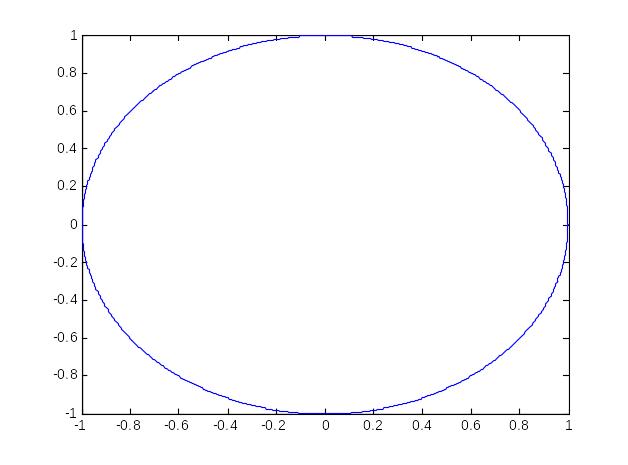
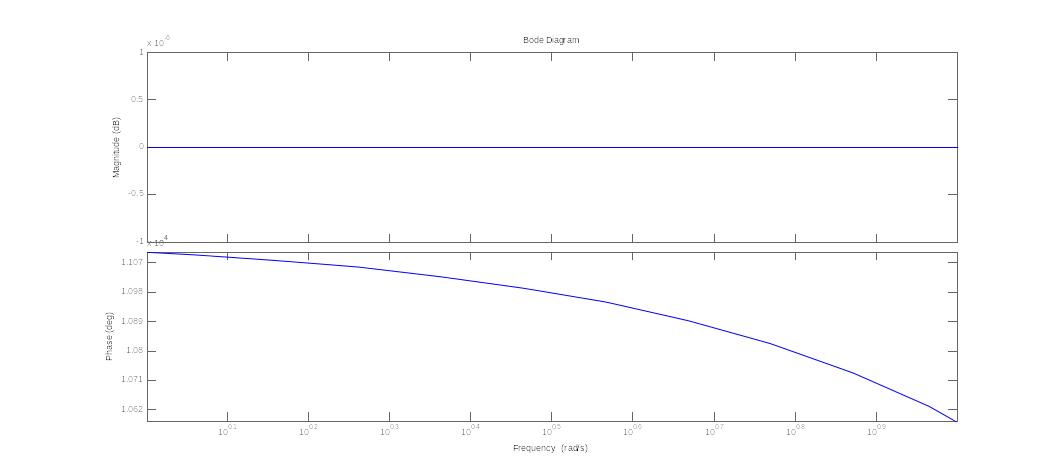
26. Отыскание аналитических выражений амплитудной и фазовой частотных характеристик и построение ЛАФЧХ сложной системы
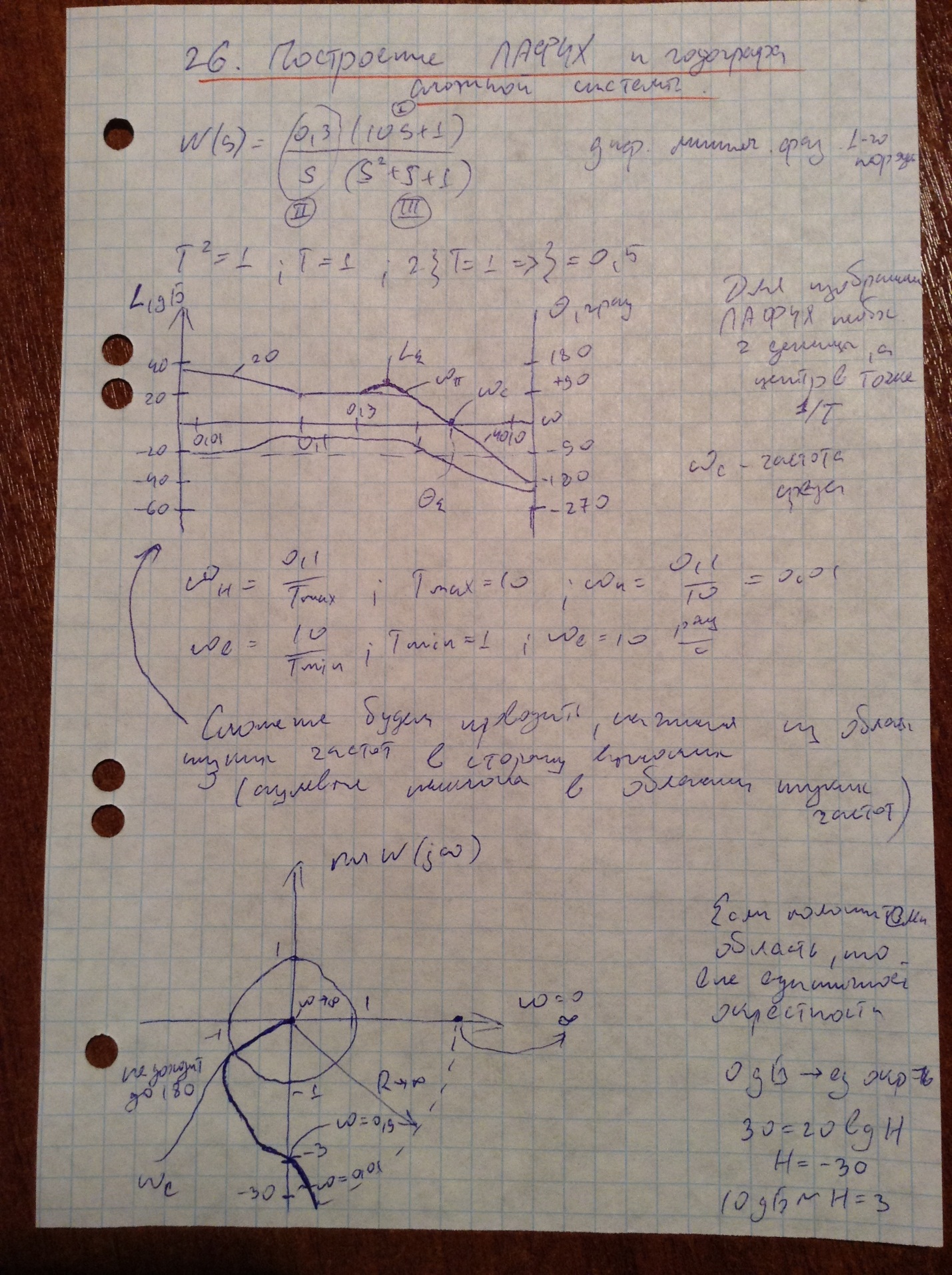
Как вопрос 16.
27. Определения асимптотической устойчивости, устойчивости и неустойчивости по методу Ляпунова
Если задана
линеаризованная автономная система
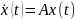 ,
то эта система имеет одно положение
равновесия, находящееся в нуле:
,
то эта система имеет одно положение
равновесия, находящееся в нуле:
 .
.
Для САУ устойчивость связана с двумя методами Ляпунова.
Положение равновесия асимптотически устойчиво, если траектория движения в n-мерном пространстве находится в какой-то точке и стремится к положению равновесия при
 .
.Если траектория движения все время находится в некоторой ограниченной области, то такое положение называется устойчивым (траектория не стремится к положению равновесия и не удаляется от него).
Если траектория, начавшись в некоторой ограниченной области вокруг положения равновесия, удаляется с течением времени от положения равновесия, то данное положение является неустойчивым.
