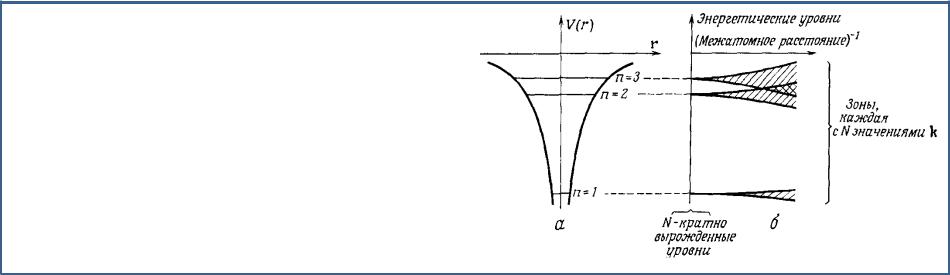
Общая формулировка метода
Так как атомные уровни хорошо локализованы, то все три слагаемых в правой части малы.
Первое и третье – потому что атомные волновые функции относятся к разным узлам, второе – потому что периодический потенциал начинает отличаться от
атомного на расстояниях, когда атомные волновые функции уже малы.
Следовательно, E k Em bm всегда мала
Это означает, что энергетический уровень в кристалле формируется из близких к нему по энергии атомных состояний
а - схематическое изображение невырожденных электронных уровней в атомном потенциале;
б – энергетические уровни для N атомов, образующих периодическую решетку, как функции обратного межатомного расстояния
Число уровней в зоне
Рассмотрим одномерный (линейный) кристалл с постоянной решетки, равной a, построенный из N элементарных ячеек.
Длина такого кристалла L=Na
Из циклических граничных условий k может принимать значения
|
2 n |
|
|
|
2 |
; |
|
|
N |
||
k |
|
; |
n 0, 1, 2,..., nmax ; |
kmin |
|
kmax |
|
nmax |
2 |
||
L |
L |
a |
|||||||||
|
|
|
|
|
|
|
|||||
Общее число возможных значений k равно N – числу элементарных ячеек
Каждая элементарная ячейка в каждой энергетической зоне дает точно одно независимое значение k.
Так как каждый электрон может независимо иметь одну из двух спиновых ориентаций, то общее число независимых состояний
(орбиталей) в каждой энергетической зоне окажется равным 2N
Зоны Бриллюэна
Первая зона Бриллюэна – элементарная ячейка Вигнера-Зейтца для обратной решётки.
Эквивалентное определение
Первая зона Бриллюэна образована совокупностью точек, которых можно достичь из начальной точки, не пересекая по пути ни одной брэгговской плоскости
Вторая зона Бриллюэна – совокупность точек, которых можно достичь из первой зоны, если пересечь всего одну брэгговскую плоскость.
n-я зона Бриллюэна – совокупность всех точек, для достижения которых из начальной точки необходимо пресечь ровно (n-1) брэгговскую плоскость.
Зоны Бриллюэна для двумерной квадратной решетки Браве
Зоны Бриллюэна некоторых трёхмерных решёток
Поверхности первой, второй и третьей зон Бриллюэна для о.ц.к. (а) и г.ц.к. (б) кристаллов. Показаны только внешние поверхности. Из определения следует, что внутренняя поверхность совпадает с внешней поверхностью
Эффективная масса
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть на электрон в кристалле действует |
||||||||||||||||||
m0 |
|
|
Fвнут |
Fвнеш |
|
|
внешнее электрическое поле E |
|||||||||||||||||||||||||||
dt |
|
|
||||||||||||||||||||||||||||||||
Работа за t |
|
|
|
e E t |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
С другой стороны: |
|
|
|
|
p; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
p |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dp |
|
|
|
|
|
|||||||||||
|
|
p p |
|
e |
E t |
|
|
|
|
|
|
|
eE |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
dt |
|
|
|||||||||||||||||||||||||
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
dp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Обобщая вывод: |
|
|
|
F |
|
|
|
Здесь |
|
p k |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
dt |
|
|
|
внеш |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
d j |
|
|
|
d |
|
|
|
|
3 |
|
2 |
|
dpi |
|
3 |
|
2 |
|
Fвнеш i |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
dt |
dt |
p |
|
p |
p |
dt |
|
|
p |
p |
|||||||||||||||||||
Далее |
|
|
|
|
j |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
j |
i |
|
|
i 1 |
|
j |
i |
|
||||||||
|
|
|
|
|
-симметричный тензор |
2 |
||
|
|
обратных эффективных масс |
|
p j pi |
|
|
второго ранга |
|
|
|
|
Эффективная масса
|
|
|
|
2 |
|
|
1 |
|
Если ввести тензор эффективных масс, |
|
|
|
|
||||
m |
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
p |
|
|
|||
|
ij |
|
|
|
||||
|
|
|
|
j |
|
i |
|
|
То уравнение движения |
3 |
d j |
|
|
* |
||||
электрона в кристалле |
mij |
|
Fвнеш i |
|
dt |
||||
можно записать в виде |
j 1 |
|
||
|
|
|
Физический смысл эффективной массы – различие между эффективной массой и массой свободного электрона обусловлено взаимодействием электрона с кристаллической решёткой
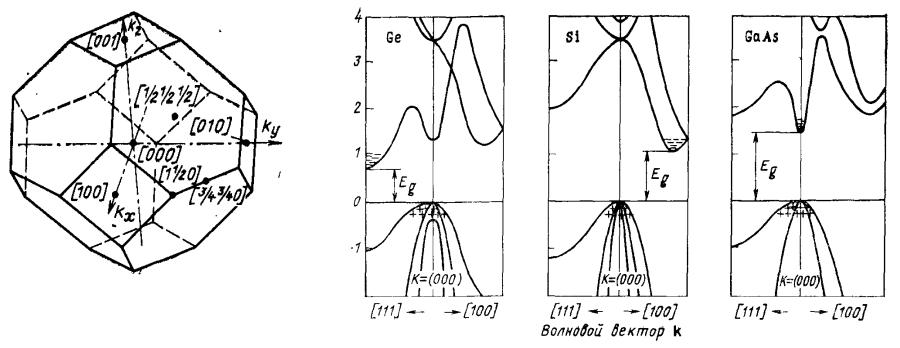
Зонная структура некоторых полупроводников
Кремний, германий, полупроводники AIIIBV (арсенид галлия, антимонид индия)
Кристаллическая структура типа алмаза ( две ГЦК, сдвинутые одна относительно другой на ¼ пространственной диагонали). В базисе 2 атома.
Первая зона Бриллюэна – четырнадцатигранник ( кубооктаэдр)
Eg Ge 0,67эВ; |
Eg Si 1,12эВ; |
Eg GaAs 1,43эВ; |
Eg InSb 0,18эВ |
Зонная структура некоторых полупроводников
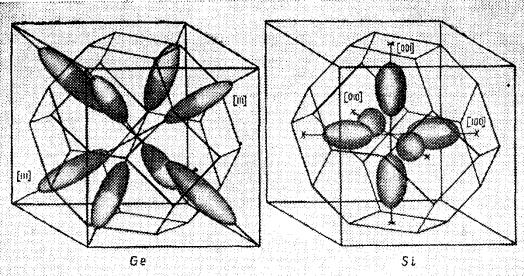
Абсолютный минимум зоны проводимости у германия расположен в направлении <111> на границе 1-й зоны Бриллюэна. Всего 8 эквивалентных минимумов. У кремния 6 эквивалентных минимумов в направлении <100> на расстоянии ¾ до границы 1-й зоны Бриллюэна
Изоэнергетические поверхности германия и кремния:
|
|
2 |
kx k0 x |
2 |
|
2 |
|
2 |
|
2 |
|
|
ky k0 y |
kz k0 z |
|
||||||
E(k ) E(k0 ) |
|
|
||||||||
|
2m1 |
|
|
|
||||||
|
|
|
|
|
|
2m3 |
|
|||
Германий: |
m1 m2 mt 0,082m0 ; |
m3 ml 1,59m0 |
|
|||||||
Кремний: |
m1 m2 mt 0,19m0 |
; |
m3 ml 0,92m0 |
|
||||||
Арсенид галлия: m 0,68m0 Поверхность постоянной энергии - сфера
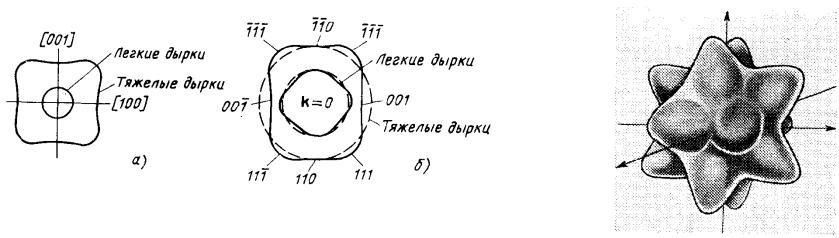
Зонная структура некоторых
полупроводников. Валентная зона
Изоэнергетические поверхности в |
|
|
валентных зонах германия (а) и |
Поверхность постоянной энергии |
|
кремния (б) |
||
тяжелых дырок в кремнии |
||
|
Валентная зона германия и кремния включает в себя три подзоны, с максимумом в центре зоны Бриллюэна (k=0). Две подзоны вырождены при k=0. Подзоны дают два типа дырок: тяжелые и лёгкие.
Германий: |
m*pт 0,33m0 ; |
m*pл 0,04m0 |
||
Кремний: |
m* |
0,56m ; m* |
0,16m |
|
pт |
0 |
pл |
0 |
|
Арсенид галлия m*pт 0,50m0 ; |
m*pл 0,12m0 |
|||