Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4625 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Национальный исследовательский ядерный университет (МИФИ)
Предмет:
Физика твердого тела
Файл:
9 Энергетические зоны в кристаллах.pptx
Скачиваний:
19
Добавлен:
15.02.2022
Размер:
718.73 Кб
Скачать
☆
►Содержание►

Волновое уравнение для электрона в периодическом потенциальном поле.

 

2

 

k 2C k UGC k G

EC k

;

Обозначим k 2k 2

 

2m

 

 

G

 

 

2m

k E C k UGC k G 0;

 

k (x) C(k G)ei k G x

 

 

 

 

G

 

 

G

 

 

 

 

Функция Блоха

 

 

 

Уравнение разделилось на N независимых уравнений для каждого k

 

Его можно переписать в виде:

 

 

 

 

 

 

 

UGC k G

Коэффициент C(k) может оказаться

 

C

k

большим, если кинетическая энергия

 

G

 

(ħ2k2/2m)

плоской волны exp(ikx) почти

 

E 2k 2 2m

 

 

 

 

равна энергии соответствующей

состоянию k(x)

Приближенное решение вблизи границы зоны Бриллюэна

Предположим UG<< (ħ2k2F/2m). Рассмотрим случай, когда k лежит точно на границе первой зоны Бриллюэна. G1/2, т.е. равен /a

 

 

k 2 12 G1 2 ;

k - G1 2 12 G1 G1 2 12 G1 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тогда на границе зоны кинетическая энергия для плоских

 

 

 

 

 

 

 

 

 

 

 

 

волн exp[ikx] и exp[i(k-G1)x] одинакова

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

k 2 2 k - G 2

2 1 G

2 ;

Значит в разложении важны

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

1

 

коэффициенты C(G1/2) и C(-G1/2).

 

 

 

 

2m

 

2m

 

2m

2

 

 

 

 

 

 

 

 

 

Остальными пренебрежём

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Уравнения примут вид:

 

 

 

 

 

 

 

 

 

 

 

UG

U G

U1

 

 

 

 

1 E C 12 G1 U1C

12 G1 0

 

 

2

 

 

 

 

 

 

2

 

 

 

 

 

 

2

 

 

1

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

1 E C 12 G1 U1C 12 G1

 

 

 

 

1 G

 

;

 

1

 

 

 

 

 

1 G

 

 

 

 

 

 

 

 

0;

1

 

 

 

2

1

 

 

 

 

 

 

 

 

2

1

 

 

 

2m

 

 

 

 

 

 

2m

 

 

 

 

Приближенное решение вблизи границы зоны Бриллюэна

Система из двух уравнений имеет нетривиальное решение для коэффициентов C(G1/2) и C(-G1/2), если определитель равен

нулю.

1 E

U1

 

0

При 1= -1 получим

 

 

2

 

1

 

 

2

 

 

 

 

1 E

2

2

;

E 1 U1

 

 

 

 

 

 

 

 

 

U1

1 E

 

 

U1

 

 

 

 

2

G1

 

U1

 

 

 

 

 

 

 

 

 

 

 

 

2m

 

 

 

Два корня: один, с энергией, меньшей кинетической энергии свободного электрона на U1 , другой – больший на U1 . Появляется энергетическая

щель шириной 2U1 на границе зоны Бриллюэна

 

C

1

2 G1

 

 

E 1

 

 

1

 

 

 

1

 

 

 

 

1

x exp i

 

G1x

exp

i

 

G1x

C 12 G1

 

 

U1

2

2

 

 

 

 

 

 

 

Одно решение – волновая функция для нижнего края энергетической щели, другая – для верхнего края. Какое именно решение отвечает меньшей энергии, зависит от знака U1

а) параболическая зависимость E(k) в одномерном случае

б) учитывается периодичность по k в) в точке, где пересекаются две параболы, появляется расщепление, вырождение снимается г) части графика, соотв. исходной параболе

д) влияние всех остальных брэгговских плоскостей (схема расширенных зон) е) уровни энергии в схеме приведённых зон ж) уровни энергии в схеме

повторяющихся зон

(из книги Ашкрофта и Мермина «Физика твёрдого тела»)

Приближенное решение вблизи границы зоны Бриллюэна

Теперь рассмотрим случай, когда волновой вектор не точно на границе зоны Бриллюэна, а близок к ней

 

 

x C k e

ikx

C k

G1 e

i k G1 x

 

 

 

 

 

 

 

 

 

 

2k 2

 

 

 

k

E C k U C k G 0

 

k

 

 

 

 

 

 

 

 

 

 

1

 

1

 

 

 

2m

 

 

k G1 E C k G1 U1C k 0;

 

 

 

 

 

 

 

 

 

k E

U1

 

0

 

E

2

 

2

0

 

 

 

 

 

U1

k G

 

E

 

 

E k G1 k k G1 k U1

 

 

 

 

1

 

 

 

 

 

 

 

 

 

E

1

k G

 

1

k G

k

2

2 12

 

k

 

 

U1

 

 

2

1

 

4

1

 

 

 

 

 

 

 

 

 

 

 

Каждый из корней описывает какую-то энергетическую зону

Приближенное решение вблизи границы зоны Бриллюэна

 

 

 

Вблизи границы зоны k

 

 

 

1

2

G k;

 

k 1

2

G

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

можно записать в виде

 

 

 

 

 

 

1

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тогда в области

 

 

 

 

2

G1

 

 

2m

 

U1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

энергий

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 2

2

1

 

 

 

 

 

 

 

 

 

 

1

 

2 2

 

 

 

 

2

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

2

 

2

 

2

 

 

1

2

 

E

 

 

 

 

G2

2

 

4

 

 

 

 

 

U 2

 

 

 

 

 

 

G1

 

U1

 

 

 

 

 

 

 

 

k

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

1

 

 

 

 

 

 

 

 

 

 

1

2m

1

 

 

 

 

2m 4

 

 

 

 

 

 

 

 

 

 

 

2m

 

 

 

 

 

2m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U1

 

Обозначив :

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Получим:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

1 G

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

E1

2 2

 

 

 

 

2

 

 

 

 

E U

 

 

 

U

 

 

 

 

 

 

 

 

 

Ek

2m

1

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

1

 

 

1

 

 

 

2m

2

1

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

1 G

 

2

 

 

 

 

 

 

 

 

 

 

 

 

Ek

E1

 

2 2

 

1

2

 

 

 

 

E U

 

 

 

 

U

 

 

 

 

 

 

 

 

 

 

 

2m

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

1

 

 

1

 

 

2m

2

1

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

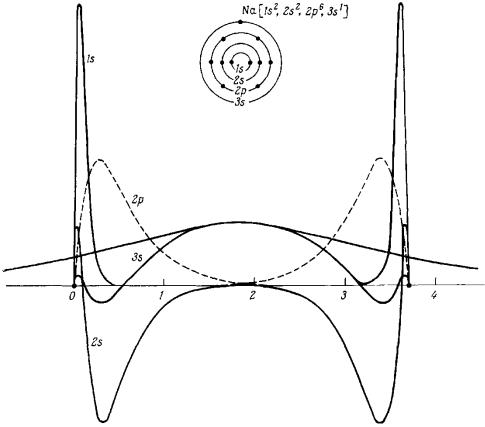
Метод сильной связи

Приближение сильной связи применимо к случаям, когда перекрытие атомных волновых функций достаточно велико, чтобы приводить к необходимости введения поправок об изолированных атомах, но в то же время не столь существенно, чтобы сделать атомное описание совершенно неправильным.

Наиболее полезно для описания энергетических зон , возникающих из частично заполненных d- оболочек атомов переходных металлов, а также для описания электронной структуры диэлектриков.

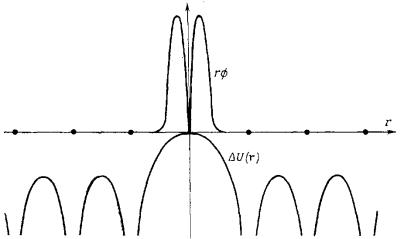
Общая формулировка метода

В окрестности каждой точки решетки полный гамильтониан H периодического потенциала можно аппроксимировать гамильтонианом Hat

отдельного атома. Hat n En n

Считаем, что связанные уровни хорошо локализованы (гамильтониан отличается от атомного на расстояниях, превышающих радиус локализации волновой функции). Тогда такая функция – хорошая аппроксимация волновой функции стационарного состояния для полного гамильтониана.

Так как у гамильтониана H периодичность решётки, n r R это справедливо и для других волновых функций

при всех векторах R решетки Браве Запишем гамильтониан в виде

 

H Hat U r

U r

- Все поправки к атомному

 

потенциалу, чтобы получить

 

полный периодический

 

потенциал кристалла

Общая формулировка метода

 

 

 

 

 

 

 

 

 

 

 

 

R

 

 

Чтобы сохранить блоховское описание

ik

 

r R e

 

 

r

 

составим N линейных комбинаций из

 

 

 

 

 

 

атомных функций

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R

 

 

 

 

 

 

 

 

 

 

 

ik

 

 

 

 

 

 

 

 

 

 

nk r e

 

 

n r R

Но такое решение тривиально.

 

R

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Предположим, что n r мала, но не строго равна нулю, там где

U r

имеет еще большое значение.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R

 

 

 

 

 

 

 

 

 

 

 

ik

 

 

 

 

 

Ищем решение в виде r e

 

 

 

r R

 

 

 

 

 

 

 

 

 

 

R

 

 

 

 

 

 

 

 

 

Где функция (r) не обязательно совпадает с атомной, но близка к ней. Тогда функцию (r) можно рассмотреть как разложение по локализованным атомным функциям

r bn n r

n

Общая формулировка метода

H r Hat U r r E k r

Умножим на m* r

Проинтегрируем по всем r и учтём, что

m* r Hat r dr Hat m r * r dr Em m* r r dr

 

 

*

 

 

 

 

*

 

 

 

 

 

 

 

 

 

 

 

 

 

r U r r dr

 

 

Получим E k Em m r r dr m

 

 

Подставляем разложения (r) и (r) и используем

 

 

*

 

 

 

 

ортонормированность атомных волновых функций

 

m r n r dr nm

 

 

 

 

 

 

 

 

 

 

 

 

*

 

 

 

 

ik R

 

 

 

E k Em bm E k Em

 

m r n r

R e

 

 

dr

bn

 

 

 

 

 

 

 

n

R 0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

*

 

 

 

 

 

 

 

 

 

 

 

 

 

m r U r n r dr bn

 

 

 

 

 

 

 

n

 

 

 

 

 

ik R

 

 

 

 

 

 

 

*

 

 

 

 

 

 

 

 

 

m r U r n r

R

e

 

 

dr bn

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

R 0

 

 

 

 

 

 

 

 

 

 

 

 

 

 
Соседние файлы в предмете Физика твердого тела
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности