Энергетические зоны
Энергетический спектр системы квазичастиц E(p) целиком определяет ее динамические свойства.
Закон для свободной частицы с массой m при скоростях, малых по сравнению со скоростью света – E=p2/(2m).
Простота закона дисперсии – следствие однородности и изотропности пространства.
Втвёрдом теле – различные точки и направления в пространстве не эквивалентны. Дисперсионное соотношение усложняется.
Втеории твёрдого тела, развитой Блохом и Пайерлсом, взаимодействие электрона с кристаллической решёткой описывается введением эффективного электрического поля с периодическим потенциалом, учитывающим симметрию кристалла
Энергетические зоны
Энергетический спектр электронов представляет собой ряд зон (полос), разделённых запрещёнными областями энергии. Эти энергетические зоны сохраняют свою индивидуальность, даже если они перекрываются.
В основе зонной теории лежат следующие приближения:
1)Твёрдое тело – идеальный периодический кристалл;
2)Равновесные положения узлов кристаллической решётки
фиксированы, т.е. ядра атомов считаются неподвижными
(адиабатическое приближение) скорость ионов 105см/с, скорость электронов 108см/с (на поверхности Ферми)
3) Многоэлектронная задача сводится к одноэлектронной –
воздействие на данный электрон всех остальных описывается некоторым усреднённым периодическим полем
Энергетические зоны
Зонная теория позволила классифицировать все кристаллы на металлы и полупроводники (диэлектрики) по признаку заполнения энергетических зон в основном состоянии
1. Вещество является металлом, т.е. проводником тока в
основном состоянии, если имеется энергетическая зона, лишь частично заполненная электронами, поскольку электроны могут ускоряться лишь при условии, что соседние вышележащие уровни энергии свободны.
2. Признак полупроводника (диэлектрика) – отсутствие частично заполненных энергетических зон. В основном состоянии не проводит ток.
Полупроводники могут стать проводниками лишь при возбуждении электронов из целиком заполненной энергетической зоны в пустую. Это собственная проводимость. Если носители заряда возбуждаются с примесных уровней – примесная проводимость.
Заполнена небольшая часть энергетической зоны – электроны. Зона почти заполнена, свободна лишь небольшая ее часть - дырки
Движение электрона в периодическом потенциале
Теорема Блоха. |
|||||
Собственные состояния одноэлектронного гамильтониана |
|||||
|
2 |
2 |
|
||
H |
|
|
U r , где U(r+R)=U(r) при всех R из решетки Браве, могут |
||
2m |
|||||
|
|
|
|||
быть выбраны так, чтобы их волновые функции имели форму плоской волны, умноженной на функцию с периодичностью решетки Браве
|
|
|
|
|
|
ikr |
|
||||
nk r e |
|
unk r , где |
unk r |
R unk r |
|
Независимые электроны, каждый из которых подчиняется одноэлектронному уравнению Шрёдингера с периодическим потенциалом, называются «блоховскими»
Доказательство теоремы Блоха
Уравнение Шрёдингера
|
|
|
2 |
|
2 |
|
|
|
где U(r) – самосогласованный |
|
|
|
U r r E r , |
||||||
|
|
|
2m |
|
|
|
|
|
периодический решеточный потенциал |
|
|
|
|
|
|
|
|
||
U r Uie r Uee r ; |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
Uie r |
- потенциал взаимодействия электрона с ионами; |
||||||||
|
|
|
|
- эффективный потенциал, описывающий усредненное |
|||||
Uee r |
|
||||||||
|
|
|
|
|
действие всех электронов на данный; |
||||
|
U r |
обладает периодичностью: U r an U r , где |
|||||||
|
|
an |
- произвольный период решётки |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
an n1a1 |
n2a2 |
n3a3 |
|
|
|||
Если r - решение уравнения Шрёдингера, то r an - тоже решение
уравнения Шрёдингера, поэтому если E – невырожденный уровень энергии ( для простоты), то
r an C r |
где C - константа |
|
|
Доказательство теоремы Блоха
Так как
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
C |
|
2 |
|
|
2 |
, |
|
|
C |
|
2 |
1 |
C e |
i a |
|
, |
где - действительная |
|||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
r |
an |
|
|
|
|
|
|
r |
|
|
|
|
|
n |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функция an |
Так как два последовательных перемещения эквивалентны одному, являющемуся их суммой, то
|
|
|
|
|
|
|
|
|
|
an - линейная функция an |
|
|
|
|
|||||||||||
C a a C a C a |
|
|
|
|
|
||||||||||||||||||||
Можно записать |
|
|
an |
k an |
Видно, что k определён с точностью до |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
вектора обратной решётки K |
K an |
2 n |
|||||||||||
Волновая функция, описывающая движение электрона в периодическом |
|
||||||||||||||||||||||||
потенциале, может быть представлена в виде |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ikr |
|
|
- плоская волна, промодулированная периодической функцией |
||||||||||||||||||||||
k r e |
|
uk r |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
В самом деле |
|
|
|
ik (r a ) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
k r an |
|
|
n |
uk r an |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
но |
|
|
|
|
|
|
ika |
|
ika |
n e |
ikr |
|
|
e |
ik r a |
|
|
||||||||
|
|
k r |
an e |
|
n k r e |
|
|
uk r |
|
n |
uk r |
|
|||||||||||||
Сравнивая эти выражения, видим, что |
|
|
u r a |
n |
u r |
|
|
|
|||||||||||||||||
|
|
|
k |
|
|
|
k |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Квазиимпульс фермиевского электрона в периодическом потенциале
Уравнение Шрёдингера для электрона в периодическом потенциале дополняется циклическими граничными условиями (ищем решение в бегущих волн)
Для простоты считаем, что кристалл имеет форму куба со стороной L
Граничные условия Борна-Кармана
x L, y, z x,
x, y L, z x,
x, y, z L x,
виде
y, z y, z y, z
1. Из граничных условий следует, что квазиимпульс электрона p k может принимать только дискретные значения, кратные 2 
L
2. Из трансляционной симметрии кристалла следует, что квазиимпульс определяется неоднозначно, с точностью до вектора обратной решетки, умноженного на постоянную Планка.
Вывод: все физически различные значения квазиимпульса содержатся в первой зоне Бриллюэна
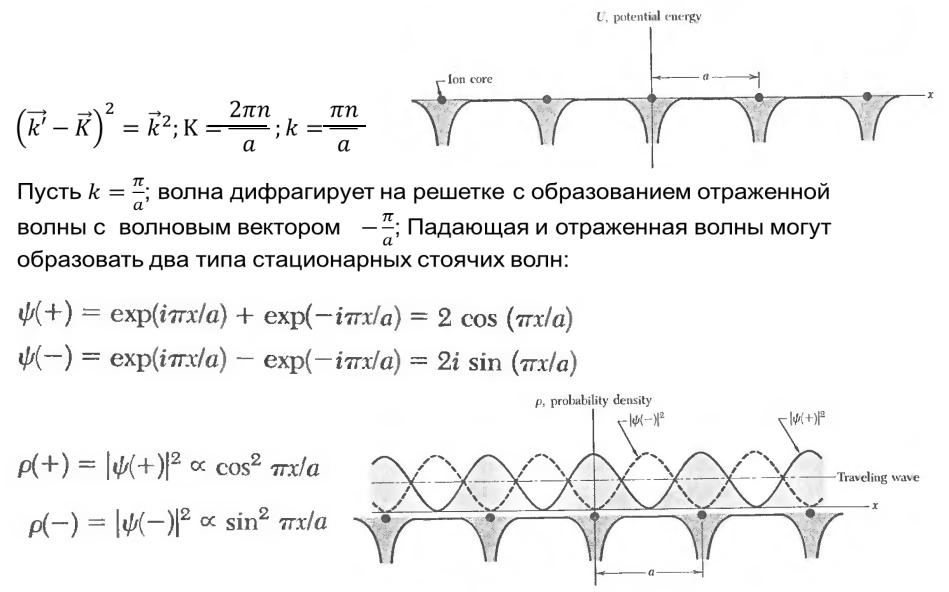
Модель почти свободных электронов
Одномерная решетка с параметром a
Условие дифракции по Бриллюэну
( ′ − )2= 2 ; K= 2 ; =
Пусть ; волна дифрагирует на решетке с образованием отраженной волны с волновым вектором ; Падающая и отраженная волны могут образовать два типа стационарных стоячих волн:
Модель почти свободных электронов
На электроны действует возмущающее слабое поле периодического потенциала ионных остовов. На основе этой модели можно объяснить общие черты зонной структуры.
Волновое уравнение для электрона в периодическом потенциальном поле.
Одномерный случай - линейная цепочка с постоянной a. U(x) – потенциальная энергия электрона, U(x)=U(x+a). Периодическую функцию можно разложить в ряд Фурье по
векторам обратной решётки G U x UGeiGx
G
Коэффициенты UG с возрастанием G быстро уменьшаются ( кулоновский потенциал как 1/G2 )
U(x) – вещественная функция,
значит U (x) U * x UGeiGx UG* e iGx U G UG*
G |
G |
|
Выберем начало координат, |
U G UG |
а значит UG UG* |
чтобы U(x) была чётной, тогда |
коэффициенты
вещественны
Волновое уравнение для электрона в периодическом потенциальном поле.
|
p2 |
|
|
2 d 2 |
UGe |
iGx |
||||
|
|
|
U (x) x |
|
|
|
|
x E x |
||
2m |
2m dx |
2 |
||||||||
|
|
|
|
G |
|
|||||
Граничные условия Борна-Кармана x L |
(x) |
|
|||||
Ищем решение в виде набора плоских волн с волновыми |
(x) C(k)eikx |
||||||
векторами, удовлетворяющими этому условию |
|
||||||
|
|
2 n |
|
n 0, 1, 2,... N |
|
k |
|
k |
; |
|
|
||||
|
|
|
|
||||
|
|
L |
2 |
|
|
||
Подставив эту функцию в уравнение, получим: |
|
|
|||||
|
2 |
k 2C k eikx UGC k ei k G x E C k eikx |
|||||
|
|||||||
k 2m |
G k |
k |
|
||||
Используем свойство ортогональности различных Фурье компонент, домножим обе стороны на exp(-ik x) и проинтегрируем по объему (длине).
Затем сделаем замену переменных k k