23. Доверительный интервал для дисперсии.

При заданной доверительной вероятности уровень значимости вычисляется по формуле: . Вычисление доверительного интервала для дисперсии анализируемой статистической совокупности производится по следующей формуле:

Проанализируем эту формулу и рассмотрим величины и выражения, входящие в эту фломулу.

В данной формуле:

• левая часть неравенства представляет собой нижнюю границу доверительного интервала:

• правая часть неравенства представляет собой верхнюю границу доверительного интервала:

Величина представляет собой несмещенную выборочную оценку дисперсии и вычисляется на основании выборочных данных по формуле:

где – выборочное среднее значение:

Доверительным интервалом называется интервал , который с заданной вероятностью содержит неизвестный оцениваемый параметр .

24. Доверительный интервал для доли.

25. Проверка статистической гипотезы о нормальном распределении выборки. Критерий хи-квадрат (Пирсона).

Критерий согласия Пирсона

Критерий Пирсона, или критерий χ²(Хи-квадрат) - применяют для проверки гипотезы о соответствии эмпирического распределения предполагаемому теоретическому распределению F(x) при большом объеме выборки (n ≥ 100). Критерий применим для любых видов функции F(x), даже при неизвестных значениях их параметров, что обычно имеет место при анализе результатов механических испытаний. В этом заключается его универсальность.

Использование критерия χ² предусматривает разбиение размаха варьирования выборки на интервалы и определения числа наблюдений (частоты) для каждого из интервалов. Для удобства оценок параметров распределения интервалы выбирают одинаковой длины. Число интервалов зависит от объема выборки.

Недостатком критерия согласия Пирсона является потеря части первоначальной информации, связанная с необходимостью группировки результатов наблюдений в интервалы и объединения отдельных интервалов с малым числом наблюдений. В связи с этим рекомендуется дополнять проверку соответствия распределений по критерию χ² другими критериями. Особенно это необходимо при сравнительно малом объеме выборки (n ≈ 100).

Статистика критерия

Для проверки критерия вводится статистика:

Где:

• . Предполагаемая вероятность попадания в i-й интервал;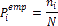

• . Соответствующее эмпирическое значение;

• n_i. Число элементов выборки из i-го интервала.

Эта величина в свою очередь является случайной (в силу случайности X) и должна подчиняться распределению χ².

Правило критерия

Если полученная статистика превосходит квантиль закона распределения χ² заданного уровня значимости α с (k - 1) или с (k -  p - 1) степенями свободы, где k - число наблюдений или число интервалов (для случая интервального вариационного ряда), а p — число оцениваемых параметров закона распределения, то гипотеза H₀ отвергается. В противном случае гипотеза принимается на заданном уровне значимости α.

26. Статистический критерий Стьюдента для сравнения выборочных средних значений.

Критерий Стьюдента применяется для проверки равенства средних значений двух выборок, сравнение количественных значений только двух выборок с нормальным распределением случайной величины. 

 Критерий Стьюдента определяется по формуле:

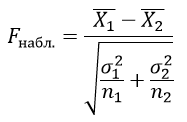
¯X1X1¯ – выборочные средние значения первой выборки;

¯X2X2¯ – выборочные средние значения второй выборки;

n₁ – объем первой выборки;

n₂ – объем второй выборки;

σ₁ и σ₂ – среднее квадратическое отклонение в соответствующих выборках и находятся из формулы:

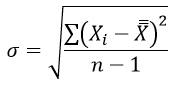
Число степеней свободы определяется по формуле:

k=n₁+n₂−2

F_кр(α, k) определяется по таблице

При F_набл<F_кр нулевая гипотеза принимается.

Формула критерия Стьюдента для несвязанных независимых выборок:

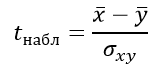
Формула для определения стандартной ошибки разности средних арифметических σ_xy:

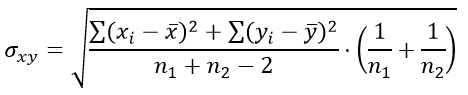
Число степеней свободы определяется выражением:

k=n₁+n₂–2

При n₁=n₂ число степеней свободы находится по формуле:

k=2n-2

а стандартная ошибка разности средних арифметических σ_xy задаётся выражением:

27. Статистические критерий Фишера для сравнения выборочных дисперсий.

Статистика Фишера

Статистика Фишера используется для проверки гипотезы о связи между объясняемым рядом и регрессорами. Используется нулевая гипотеза: коэффициенты при всех регрессорах равны нулю.

Формула для расчёта статистики Фишера для модели с константой:

Формула для расчёта статистики Фишера для модели без константы:

Где:

• R². Коэффициент детерминации;

• k. Количество факторов, включенных в модель (включая константу);

• N. Количество наблюдений.

Для нецентрированного коэффициента детерминации может быть рассчитана соответствующая статистика Фишера.

Вероятность статистики Фишера

Статистика Фишера имеет распределение Фишера:

• для модели с константой: F(k - 1, N - k);

• для модели без константы: F(k, N - k).

Нулевая гипотеза о равенстве нулю коэффициентов при всех регрессорах отклоняется, если вероятность меньше, чем уровень значимости. Рассматривают один из стандартных уровней значимости 0.1, 0.05 или 0.01.

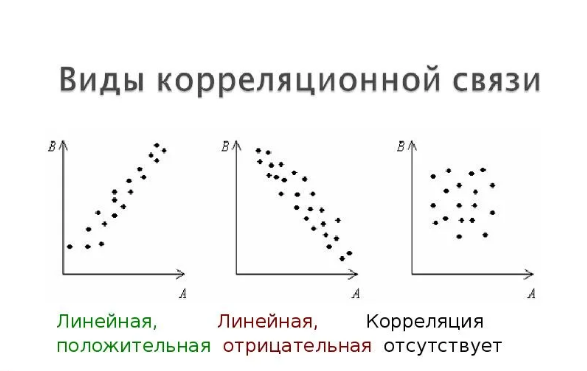
28. Виды зависимостей случайных величин. Анализ статистических зависимостей. Корреляционное поле.

Каждая единица наблюдения в выборочной совокупности характеризуется двумя измеренными признаками. В декартовой системе координат каждая i-тая единица наблюдения из выборочной совокупности может быть представлена точкой на плоскости, с координатами 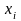и (значения и являются результатами измерения признаков X и Y). В результате такого отображения всех единиц наблюдения из выборочной совокупности точками на плоскости в прямоугольной системе координат будет получено облако точек.

Полученное в прямоугольной системе координат облако точек, являющихся отображением единиц наблюдения из выборочной совокупности, называется корреляционным полем. Визуальный анализ корреляционного поля позволяет сделать предположения о характере связи и степени ее выраженности.