Нормальное распределение.
Нормальным называется распределение вероятностей, которое для одномерного случая задаётся функцией Гаусса.
Нормальное распределение играет важнейшую роль во многих областях знаний. Случайная величина подчиняется нормальному закону распределения, когда она подвержена влиянию большого числа случайных факторов, что является типичной ситуацией в анализе данных. Поэтому нормальное распределение служит хорошей моделью для многих реальных процессов.
Нормальное распределение зависит от 4-х параметров:
математическое ожидание — «центр тяжести» распределения;
дисперсия — степень разброса случайной величины относительно математического ожидания;
коэффициент асимметрии — параметр формы распределения, определяющий его симметрию относительно математического ожидания;
коэффициент эксцесса — параметр распределения, задающий «остроту» пика распределения.
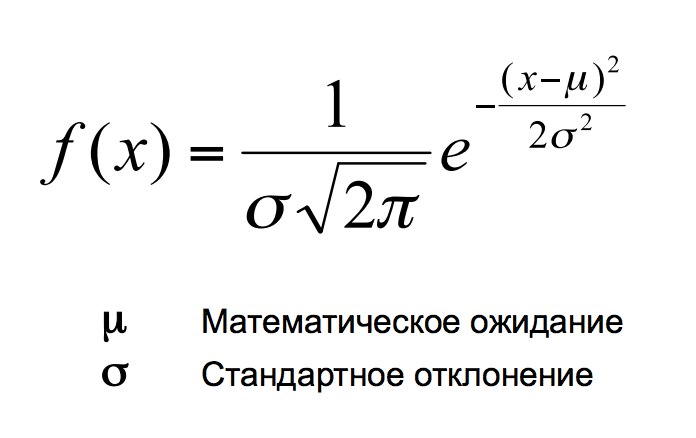
Выборочный метод статистического исследования. Генеральная и выборочная совокупности.
Выборочный метод – статистический метод исследования общих свойств совокупности каких-либо объектов на основе изучения свойств лишь части этих объектов. Совокупность исследуемых объектов, интересующих исследователя, называет генеральной совокупностью. А часть объектов, подлежащих изучению, называют выборочной совокупностью или выборкой.
Главная задача выборочного обследования – с минимальным объемом выборки получить как можно более точное описание интересующей генеральной совокупности на основе выборочных данных. Добиться этого можно только на основе репрезентативной выборки, т.е. выборки объективно отражающей свойства генеральной совокупности.
Генеральная совокупность — вся изучаемая выборочным методом статистическая совокупность объектов и/или явлений общественной жизни (единиц отбора), имеющих общие качественные признаки или количественные переменные. Выборочная совокупность (выборка) — представительная часть генеральной совокупности.
Вариационный ряд. Графическое представление вариационного ряда: полигон частот и гистограмма.
Вариационными рядами называют ряды распределения, построенные по количественному признаку. Любой вариационный ряд состоит из двух элементов: вариантов и частот.
Вариантами считаются отдельные значения признака, которые он принимает в вариационном ряду.
Частоты – это численности отдельных вариантов или каждой группы вариационного ряда, т.е. это числа, показывающие, как часто встречаются те или иные варианты в ряду распределения. Сумма всех частот определяет численность всей совокупности, её объём.
Частостями называются частоты, выраженные в долях единицы или в процентах к итогу. Соответственно сумма частостей равна 1 или 100 %. Вариационный ряд позволяет по фактическим данным оценить форму закона распределения.
Точечные оценки математического ожидания и дисперсии.
Показатели вариации: размах, среднее линейное отклонение, среднее квадратичное отклонение, дисперсия.
Размах вариации — это разность между максимальным и минимальным значениями признака
Среднее линейное отклонение — это средняя арифметическая из абсолютных отклонений отдельных значений признака от средней.
Среднее
квадратическое отклонение (
)
равно квадратному корню из среднего
квадрата отклонений отдельных значений
признака от средней арифметической:
Дисперсия
представляет собой средний квадрат
отклонений индивидуальных значений
признака от их средней величины.
Относительные показатели вариации: коэффициент вариации, коэффициент осцилляции, линейный коэффициент вариации.
Коэффициент осцилляции
Относительное линейное отклонение
Коэффициент вариации
Интервальные оценки. Доверительный интервал для математического ожидания.
В математической статистике интервальной оценкой называется результат использования выборки для вычисления интервала возможных значений неизвестного параметра, оценку которого нужно построить. Следует отличать от точечной оценки, которая даёт лишь одно значение. Самым распространенным видом интервальных оценок являются доверительные интервалы.
Доверительный интервал для математического ожидания - это такой вычисленный по данным интервал, который с известной вероятностью содержит математическое ожидание генеральной совокупности. Естественной оценкой для математического ожидания является среднее арифметическое её наблюденных значений.
