8. Независимость случайных событий и правило произведения вероятностей.

Если событие А не зависит от В, то и наоборот, т.е. свойства независимости событий взаимны. И тогда условная вероятность каждого из событий равна безусловной его вероятности.

Тогда вероятность совместного наступления/умножения/пересечения событий равна:

9. Формула полной вероятности.

Рассмотрим зависимое событие  , которое может произойти лишь в результате осуществления одной из несовместных гипотез  , которые образуют полную группу. Пусть известны их вероятности   и соответствующие условные вероятности  . Тогда вероятность наступления события   равна:

Эта формула получила название формулы полной вероятности.

10. Формула Байеса.

Формула Байеса (или теорема Байеса) (англ. Bayes' theorem) — соотношение различных предполагаемых вероятностей различных событий, которое дает вероятность, что какое-то событие A является результатом X ряда независимых друг от друга событий B1,B2…Bn, который, возможно, привел к A.

11. Схема испытаний и формула Бернулли.

Рассмотрим важный частный случай: проводятся n одинаковых независимых испытаний с двумя исходами А или Ā. Вероятности P(А)=p и P(Ā)=1-p=q постоянны и не равны ни нулю, ни единице. Такие испытания иногда называют испытаниями Бернулли, исход А – успех, а исход Ā – неудача.

По теореме умножения вероятностей независимых событий для каждого элементарного события найдем вероятность, равную произведению вероятностей результатов отдельных испытаний: pkqn-k, где k– количество опытов, в которых произошло событие A, (n-k) – количество опытов, в которых произошло событие Ā.

Якоб Бернулли впервые доказал, что вероятность того, что событие A наступит ровно k раз из n, равна P(k) = Cnkpkqn-k, k=0, 1, 2 … n, Cnk– число сочетаний из n по k.

Эта формула называется «формулой Бернулли», а модель, описывающая совокупный результат n независимых испытаний с двумя исходами (А или Ā) называется «схемой Бернулли».

12. Дискретная случайная величина. Функция распределения дискретной случайной величины.

Дискретная (прерывная) случайная величина – принимает отдельно взятые, изолированные значения. Количество этих значений конечно либо бесконечно, но счётно.

Для описания дискретной случайной величины (ДСВ) используется закон ее распределения, по которому каждому значению ДСВ ставится в соответствие вероятность появления этого значения.

Таблица 1. Закон распределения ДСВ

Значения ДСВ	x1	x2	x3	…	xn
Вероятности	p1	p2	p3	…	pn

13. Непрерывная случайная величина. Функция распределения непрерывной случайной величины. Функция плотности распределения случайной величины.

Для описания дискретной случайной величины (ДСВ) используется закон ее распределения, по которому каждому значению ДСВ ставится в соответствие вероятность появления этого значения.

Таблица 1. Закон распределения ДСВ

Значения ДСВ	x1	x2	x3	…	xn
Вероятности	p1	p2	p3	…	pn

Дадим определение непрерывной случайной величины (НСВ).

Пусть задан конечный или бесконечный интервал на числовой оси. Этот интервал содержит бесконечное число действительных чисел. Случайная величина называется непрерывной, если в результате испытания ее значение может быть любым действительным числом из заданного интервала. Число возможных значений непрерывной случайной величины – бесконечно.

Типичным примером НСВ может являться результат измерения исследуемой физической величины: температуры среды, давления в сосуде, массы тела, электрического тока в цепи, электрического напряжения на участке цепи и т.д.

Очевидно, что представленный в таблице 1 закон распределения ДСВ использовать для описания НСВ практически не представляется возможным по причине бесконечно большого числа значений НСВ.

Для описания НСВ используется другой подход. В основе этого подхода лежит определение вероятности события, состоящего в том, что случайная величина X будет меньше некоторого заданного значения x . Очевидно, что вероятность PX  x будет являться функцией от x .

Функцией распределения случайной величины X называется функция Fx , которая определяет вероятность события, состоящего в том, что случайная величина X будет меньше значения x . Формальная запись этого определения имеет следующий вид PX  x  Fx. Функцию Fx также называют интегральной функцией или интегральным законом распределения случайной величины X .

14. Математическое ожидание и дисперсия случайной величины.

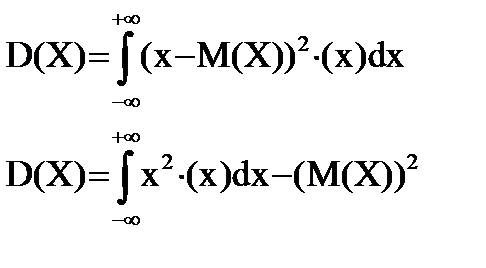
15. Биномиальное распределение.

Биноминальное распределение - распределение количества «успехов» в последовательности из n независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна p.

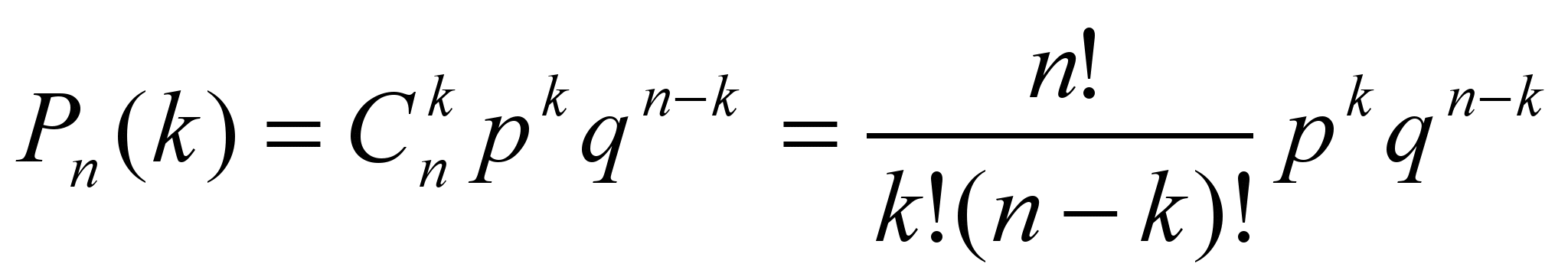(вместо k будет m)