Вероятность события. Классическое определение вероятности. Геометрическое определение вероятности. Статистическое определение вероятности.
Вероятность — степень (относительная мера, количественная оценка) возможности наступления некоторого события.
Вероятность события является основным понятием ТВ. Рассмотрим пример: в коробке находятся 6 одинаковых шаров, из них 2-красные, 3-синие, 1-белый. Испытание состоит в извлечении наугад шара из коробки. Очевидно, что вероятность вытащить цветной шар выше вероятности вытащить белый. Появление цветного шара – событие A. Число, характеризующее возможность события А – вероятность этого события. В этом испытании возможно 6 ЭС, они образуют ПГС, т.е. они попарно несовместные, поскольку шары извлекаются наугад, имеют одинаковую форму и тщательно примешиваются, значит ЭС являются равновозможными.
ЭС w2-w6, в которых событие А произошло, называются благоприятствующими этому событию. Формально, событие А можно определить, как сумму/объединение пяти несовместных и равновероятных ЭС.
Классическое определение вероятности.
Вероятностью P(A) события A называется отношение числа m элементарных исходов испытания, благоприятствующих событию А, n общему числу возможных равновероятных и несовместных элементарных исходов.
Значение ВС лежит в 0<=P(A)<=1.
Относительная частота событий. Статистическое определение ВС.
ОЧС наряду с ВС является основным понятием ТВ. ОЧС или статической частотой f(A) события А называется отношения числа испытаний n в которых событие А произошло общему числу проведённых испытаний N.
f(A)=
Классическое определение вероятности предполагает равновозможные ЭС и не требует проведения испытаний, т.е. эта вероятность – априорная, а статистическая – апостериорная.
ОЧС обладает свойством, называемым свойством статистической устойчивости: с увеличением числа опытов (т.е. с увеличением n) частота события принимает значения, близкие к вероятности этого события р.
Статистической вероятностью p(A) называется неизвестное число, около которого сосредоточены значения статистической частоты f(A) при возрастании числа испытаний N.
Теоретически при N->∞ ОЧС f(A)->p(A).
Статистическая вероятность p(A) определяется с заданной точностью в результате проведения большого числа испытаний.
Геометрическое определение вероятности.
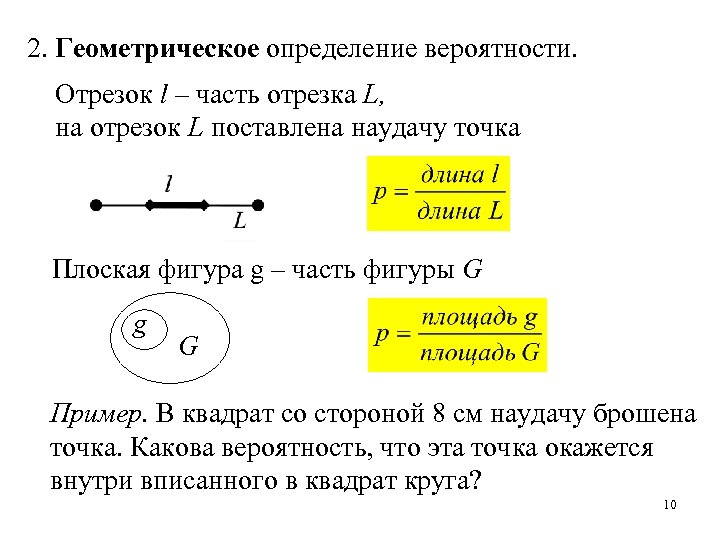
Операции над вероятностями. Вероятность объединения несовместных событий
Рассмотрим несовместные события А1 и А2. Суммой/объединением А1+А2 называется событие, которое состоит в появлении либо события А1, либо А2.
Определение: вероятность суммы/объединения двух несовместных событий равно сумме вероятностей этих событий.
Вероятность объединения совместных событий.
Если события А1 и А2 совместные, то их объединением будет такое событие в котором появляются одновременно оба этих события.
Условные вероятности.
Пусть в результате испытания могут произойти события А и В, причём их объединение невозможно.
Условной вероятностью Р(В/А) называют вероятность события В, которое вычисляется в предположении, что событие А уже произошло. (Аналогично с Р(А/В)).
