Экзамен 2021 / Панков Пособие по ТВиМС часть 2

Пусть для получения оценки a* математического ожидания a случайной величины было произведено n независимых испытаний (разыграно n

возможных значений ) и по ним было найдено выборочное среднее x, которое принято в качестве искомой оценки:

a* x.

Ясно, что если повторить опыт, то будут получены другие возможные значения , следовательно, другое среднее, а значит, и другая оценка a*. Уже отсюда следует, что получить точную оценку математического ожидания невозможно. Естественно, возникает вопрос о величине допускаемой ошибки. Ограничимся отысканием лишь верхней границы допускаемой ошибки с заданной вероятностью (надежностью) :

P x a .

Интересующая нас верхняя граница ошибки является не чем иным, как «точностью оценки» математического ожидания по выборочному среднему при помощи доверительных интервалов, о которой уже шла речь в теме 13. Поэтому воспользуемся результатами, полученными ранее, и рассмотрим для примера случай, когда случайная величина распределена нормально и ее дисперсия 2 известна.

В этом случае с надежностью верхняя граница ошибки (см. пример 1 из темы 13)

t 1 /2 ,

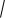n

где n – число испытаний (разыгранных значений ), а

1 / 2.

Пример. Пусть нужно с надежностью 0,95 найти верхнюю границу ошибки , если для оценки математического ожидания нормальной случайной величины с известной дисперсией 0,25 было разыграно 100 возможных значений .

Итак, n 100, 0,5, 1 2 0,975 . Из таблиц математической статистики

Разыгрывание дискретной случайной величины

Пусть требуется разыграть или смоделировать дискретную случайную величину , т. е. получить последовательность ее возможных значений xi ,

51

Обозначим через R непрерывную случайную величину, распределенную равномерно в интервале 0,1 , а через ri , i , ее возможные значения, т. е.

случайные числа.

Разобьем промежуток 0 R 1 на оси абсцисс декартовой системы координат

промежуток j , ставить в соответствие возможное значение xj , то разыгрываемая величина будет иметь заданный закон распределения

Правило. Для того, чтобы разыграть дискретную случайную величину, заданную таблицей распределения

надо

1) разбить промежуток 0,1 оси абсцисс на n промежутков:

2) выпишем из таблицы восемь случайных чисел (или сгенерируем с помощью вычислительной техники), например:

0,37; 0,10; 0,08; 0,99; 0,12; 0,66; 0,31; 0,85.

52

Случайное число r1 0,37 принадлежит частичному интервалу 2 , поэтому разыгрываемая дискретная случайная величина приняла возможное значение x1 11. Аналогично получим остальные возможные значения.

Итак, разыгранные возможные значения таковы: 11; 3; 3; 24; 3; 24; 11; 24.

Разыгрывание непрерывной случайной величины. Метод обратных функций

Пусть требуется разыграть непрерывную случайную величину , т. е. получить последовательность ее возможных значений xi , i 1,n, зная функцию распределения F x .

Теорема. Если ri – случайное число, то возможное значение xi разыгрываемой непрерывной случайной величины с заданной функцией распределения F x , соответствующее этому ri , является корнем уравнения

F xi ri .

Доказательство. Пусть выбрано случайное число ri (0 ri 1). Так как в интервале всех возможных значений функция распределения F x монотонно

возрастает от 0 до 1, то в этом интервале существует, причем только одно, такое значение аргумента xi , при котором функция распределения примет значение ri . Другими словами, уравнение F xi ri имеет единственное решение xi F 1 ri .

Докажем теперь, что корень xi уравнения F xi ri является возможным значением непрерывной случайной величины (временно обозначим ее через ,

интервале всех возможных значений , то в этом интервале большим значениям аргумента соответствуют большие значения функции, и обратно. Поэтому, если c xi d , то

F c ri F d .

Из этих неравенств следует, что если случайная величина заключена в интервале c d , то случайная величина R U 0,1 заключена в интервале

F c R F d и обратно. Таким образом, равносильны и равновероятны

P c d P F c R F d .

53

Так как величина R распределена равномерно в интервале 0,1 , то вероятность попадания R в некоторый интервал, принадлежащий интервалу0,1 , равна его длине. В частности,

P F c R F d F d F c .

Следовательно,

P c d F d F c .

Итак, вероятность попадания в интервал c,d равна приращению функции распределения F x на этом интервале, а это означает, что

словами, числа xi , определяемые формулой F xi ri , являются возможными значениями величины с заданной функцией распределения F x .

Теорема доказана.

Правило 1. Для того, чтобы найти возможное значение xi непрерывной случайной величины , зная ее функцию распределения F x , надо выбрать случайное число ri приравнять его функции распределения и решить отно-

сительно xi , полученное уравнение

F xi ri .

Заметим, что если решить это уравнение в явном виде не удается, то прибегают к графическим или численным методам.

Пример. Нужно разыграть 3 возможных значения непрерывной случайной величины , распределенной равномерно в интервале 2,10 .

Для решения данной задачи запишем функцию распределения величины , распределенной равномерно в интервале 2,10 :

F x x 8 2 .

Используя правило 1, напишем уравнение для отыскания возможных значений F x , для чего приравняем функцию распределения случайному

числу: xi 8 2 ri .

Отсюда xi 8ri 2.

Выберем 3 случайных числа, например, 0,11; 0,17; 0,66. Подставим эти числа в уравнение, разрешенное относительно xi , в итоге получим соответствующие возможные значения : x1 8 0,11 2 2,88 ; x2 3,36; x3 7,28.

Правило 2. Для того, чтобы найти возможное значение xi непрерывной случайной величины , зная ее плотность вероятности

случайное число ri и решить относительно xi уравнение

xi

p x dx ri .

54

Пример. Пусть задана плотность вероятности непрерывной случайной величины

в интервале 0, / 2 ; вне этого интервала p x 0 .

Требуется найти явную формулу для разыгрывания возможных значений . Для решения этой задачи напишем в соответствии с правилом 2 уравнение

x0i 1 2x dx ri .

Выполнив интегрирование и решив полученное квадратное уравнение относительно xi , окончательно получим

xi 2 1 1 ri .

55

Литература ко II части

Основная литература:

1.Неделько, С. В. Типовые задачи математической статистики : учебное пособие / С. В. Неделько, В. М. Неделько, Г. Н. Миренкова. — Новосибирск : Новосибирский государственный технический университет, 2014. — 52 c. — ISBN 978-5-7782-2481-0. — Текст : электронный // Электронно-библиотечная система IPR BOOKS : [сайт]. — URL: http://www.iprbookshop.ru/45451.html\

2.Седаев, А. А. Теория вероятностей и математическая статистика : учебное пособие / А. А. Седаев, В. К. Каверина. — Воронеж : Воронежский государственный архитектурно-строительный университет, ЭБС АСВ, 2015. — 132 c. — ISBN 2227-8397. — Текст : электронный // Электронно-библиотечная система IPR BOOKS : [сайт]. — URL: http://www.iprbookshop.ru/55060.html

Дополнительная литература:

1. Монсик, В. Б. Вероятность и статистика : учебное пособие / В. Б. Монсик, А. А. Скрынников. — 4-е изд. — Москва : Лаборатория знаний, 2020. — 382 c.

— ISBN 978-5-00101-858-2. — Текст : электронный // Электронно-библиотеч-

ная система IPR BOOKS :[сайт]. — URL: http://www.iprbookshop.ru/6463.html

56

57

План УМД на 2020/21 уч.г. С. __, п. __

Константин Николаевич Панков

ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

ЧАСТЬ 2

Учебное пособие

Подписано в печать __.__.2021г. Формат 60х90 1/16. Объём усл.п.л. Тираж экз. Изд. № . Заказ

58