Экзамен 2021 / Панков Пособие по АСП

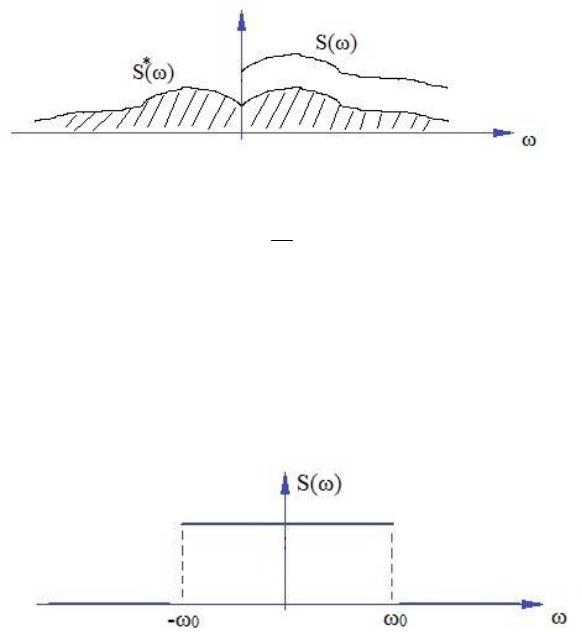
В силу связи автокорреляционной функции с нормированной автокорреляционной функцией, понятия спектральной и нормированной спектральной плотности, введенной ранее очень близки.

На приведенном ниже рисунке спектральная плотность в комплексной области обозначена со звездочкой S*( ):

K τ S ei τd

S( ) 1 K τ e i τdτ 2π

Эти две формулы называются формулами (или теоремой) Винера-Хинчина. Теорема Винера-Хинчина эквивалентна теореме Бохнера-Хинчина (с точностью до замены автокорреляционной функции на нормированную

автокорреляционную)

Пример. Найти автоковариационную функцию идеального низкочастотного процесса, у которого спектральная плотность имеет вид:

21

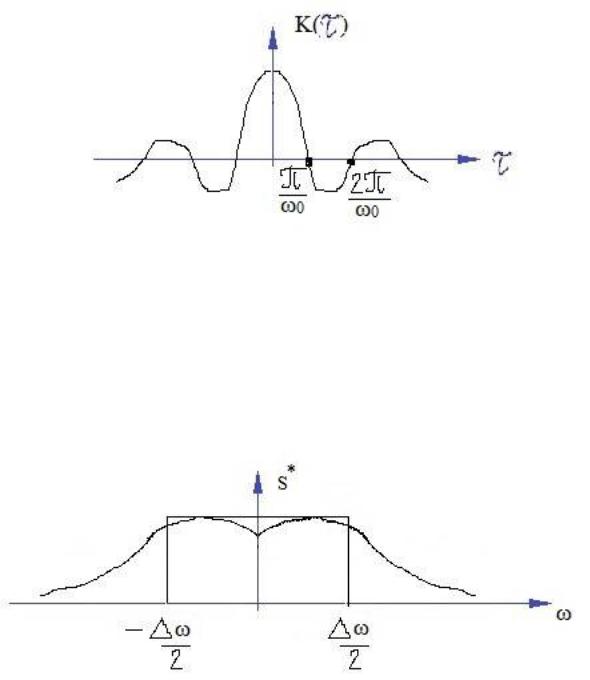
Определение. Эффективной шириной спектра называется величина равная:

DX maxS* S* d

Т.е. площадь под графиком плотности заменяется площадью прямоугольника с высотой S (ω) и шириной Δω:

Аналогично можно ввести

Определение. Эффективной длительностью автокорреляционной функции

(или интервалом корреляции) называется величина Δτ равная:

стационарного в широком смысле случайного процесса.

22

В этом случае площадь под графиком модуля нормированной автокорреляционной функции заменяется площадью прямоугольника с шириной равной Δτ и высотой равной единице.

Обратим внимание, что в этом определении используется нормированная автокорреляционная функция (для этого мы разделили автокорреляционную функцию K на дисперсию DX . А высота прямоугольника равна

максимумум нормированных автокорреляционных функций, который равен значению этой функции в нуле, и равен единице.

Величина Δτ дает ориентировочное представление о том, на каком интервале времени имеет место коррелированность между значениями сечений случайного процесса.

Определение. Дельта-функций Дирака называется функция, определенная как:

Таким образом, дельта-функция при всех значениях аргумента отличных от нуля равна нулю, а при нуле равна бесконечности.

Отметим, однако, что с точкой бесконечность нельзя обращаться как с числом. В данном случае, это символическое изображение, заданное определением, т. е. высота прямоугольника единичной площади, у которого ширина основания стремится к нулю.

Свойства δ x :

2. Фильтрующее свойство :

23

f * 0 d f 0

Пример. Найти спектральную плотность гармонического колебания со случайной начальной фазой:

X t Acos 0t ,

где A и 0 – постоянные, а φ - случайная величина, равномерно распределенная на интервале [0, 2π].

Легко можно найти (было показано в примере в подтеме о линейных преобразованиях) автокорреляционную функцию K(τ) этого случайного процесса:

Для удобства вычисления в комплексном пространстве здесь косинус мы заменили через экспоненты по формуле Эйлера.

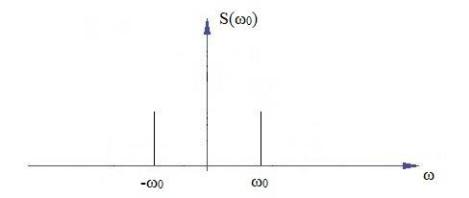
На рисунке изображен спектр случайного процесса в комплексной форме. В действительной форме нужно отбросить отрицательные частоты, а амплитуду при 0 увеличить в два раза.

Белый шум

Определение. Случайный процесс t,t называют белым шумом, если

он является стационарным в широком смысле и обладает постоянной спектральной плотностью c, называемой интенсивностью белого шума:

S S0 с constдля ;

Найдем автокорреляционную функцию белого шума.

Следовательно, любые два сечения белого шума X(t1) и X(t2) при t1≠t2 некоррелированные, т.к. К(τ) = 0, при τ= t1-t2 ≠ 0.

24

Белый шум это удобная математическая абстракция, так как физически такой процесс не реализуем – у него дисперсия равна бесконечности. С помощью этой математической модели упрощается решение многих практических задач. Обращаться к этой модели можно, когда все временные характеристики процесса много больше, чем интервал корреляции и можно считать, что выполняется условие: «Любые два сечения X(t1) и X(t2) при t1≠t2 некоррелированные (слабо коррелированы).

Случайный процесс назвали «белым» по аналогии с белым светом, у которого спектр электромагнитного излучения имеет равномерную мощность по всем длинам волн в видимой части спектра.

состояния в j-е за 1 шаг в момент времени n.

Определение. Цепь Маркова называется однородной во времени, если ее

любой момент времени n.

В дальнейшем мы будем рассматривать однородные цепи Маркова. Определение. Цепь Маркова - конечная, если фазовое пространство E –

конечно (в противном случае цепь Маркова счетна). Обозначим

25

|| pij ||N N ,

где N – мощность фазового пространства E, и назовем ее матрицей переходных вероятностей за 1 шаг.

Обозначим через p вектор

p P 0 i ;i E .

Вектор p - распределение случайной величины 0 . Назовем вектор p

начальным вектором (начальным распределением) цепи Маркова.

Набор ( p,П) полностью определяет однородную цепь Маркова.

Обозначим через pij n P l n j | l i переходную вероятность из i – го состояния в j – е за n шагов.

В силу однородности цепи Маркова величина pij n не зависит от l.

Введем матрицу переходных вероятностей за n шагов: n || pij n ||N N .

С помощью формулы полной вероятности докажите самостоятельно, что

pij n pik n 1 pkj . k E

Это равенство называется уравнением Колмогорова – Чепмена.

В матричном виде оно будет выглядеть следующим образом:

n n 1 .

Очевидно, что выполняется равенство

Примеры. 1. Предположим, что некоторая частица, двигаясь по целочисленным точкам отрезка 1,N , в дискретные моменты времени может

совершать скачки влево или вправо на один шаг.

Вероятность скачка влево равна p 0 из любой внутренней точки

k 2,N 1, равна 1 из точки 1 и равна 0 из точки N .

26

Вероятность скачка вправо равна q 1 p 0 из любой внутренней точки k 2,N 1, равна 0 из точки 1 и равна 1 из точки N .

Пусть n - точка, характеризующая положение частицы в момент времени n 0 .

Легко видеть, что последовательность n,n 0 образует цепь Маркова.

Эта цепь называется случайным блужданием с отражающими экранами.

В качестве левого и правого отражающих экрана выступают концевые точки

2. Изменим свойства экранов в предыдущем примере. Пусть теперь из точки 1 можно произвести скачок вправо с вероятностью , а с вероятностью 1 можно остаться в точке 1. Из точки N можно произвести скачок влево с вероятностью , а с вероятностью 1 можно остаться в точке N . Остальные условия оставим без изменения.

Последовательность n,n 0 так же образует цепь Маркова с матрицей переходных вероятностей:

Если 0 1, то это случайное блуждание с упругими экранами, а если0 - это случайное блуждание с поглощающими экранами.

Классификация состояний цепи Маркова

Пусть E1,E2,... - состояния цепи Маркова.

27

Определение. Состояние Ej называется несущественным, если найдется состояние Ek и натуральное число m такие, что pjk m 0, но pkj n 0 при любых n . В противном случае состояние Ej - существенное.

Пример. При случайном блуждании с поглощающими экранами состояния 1 и N существенные, а остальные – несущественные. При случайном блуждании с упругими и отражающими экранами все состояния существенны.

Определение. Существенные состояния Ej и Ek называются

сообщающимися, если существуют m,n такие, что pjk m 0 и pkj n 0.

Пример. При случайном блуждании с упругими и отражающими экранами все состояния существенные и сообщающиеся.

Докажите самостоятельно, что отношение сообщаемости является отношением эквивалентности.

Обозначим через S0 класс несущественных состояний данной цепи Маркова. Существенные состояния разбиваются на непересекающиеся подклассы по отношению сообщаемости. Обозначим эти подклассы S1, S2 и т.д. Перенумеруем состояния из фазового пространства так, чтобы первые номера были в S0 , вторые – в S1 и т. д. Для конечной цепи Маркова это можно сделать. В матрице переходных вероятностей переставятся строки и столбцы, и она приобретет вид:

Определение. Если какой-либо класс сообщающихся состояний состоит из одного состояния, то оно называется поглощающим состоянием.

28

Пример. При случайном блуждании с поглощающими экранами состояния 1 и N - поглощающие.

Определение. Во введенных выше обозначениях классы S1,S2,...

называются эргодическими подклассами существенных состояний, S0 – классом несущественных состояний.

Определение. Если все фазовое пространство цепи Маркова составляет один эргодический подкласс сообщающихся состояний, то эта цепь называется

неприводимой или неразложимой.

Пример. При случайном блуждании с упругими или отражающими экранами цепи Маркова являются неприводимыми.

Определение. Существенное состояние Ej называется периодическим с периодом dj , если dj - это наибольший общий делитель всех таких натуральных n, что pjj n 0.

Пример. Пусть некоторая частица, двигаясь по целочисленным точкам отрезка 1,N , в дискретные моменты времени может совершать скачки вправо

на один шаг, если она находилась в точке k 1,N 1, а из состояния N она совершает скачок в 1. Пусть n - точка, характеризующая положение частицы в момент времени n 0 . Легко видеть, что последовательность n,n 0

образует цепь Маркова, а все ее состояния – существенные и сообщающиеся, а d1 ... dN N .

Определение. Существенное состояние Ej с периодом dj 1 называется

ациклическим.

Утверждение (без доказательства). Все состояния неприводимой цепи Маркова имеют одинаковый период.

Определение. Неприводимая цепь Маркова, в фазовом пространстве которой все состояния ациклические, называется ациклической.

Всякой конечной однородной цепи Маркова с матрицей переходных

неприводимости цепи Маркова необходима сильная связность графа переходов. Эргодические подклассы составляет компоненты сильной связности орграфа, а несущественные состояния лежат на подходах к ним.

Смена состояний в конечной однородной цепи Маркова эквивалентна переходу от вершины к вершине в конечном графе в соответствии с вероятностями, заданными весами на дугах. Такие процессы задают случайное блуждание на графе.

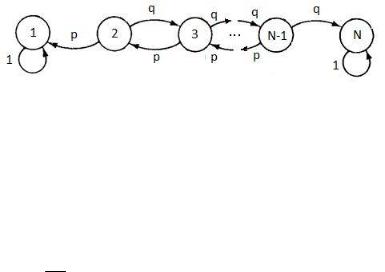
Пример. При случайном блуждании с поглощающими экранами граф переходов выглядит следующим образом:

29

Эргодическая теорема для неприводимых цепей Маркова

Докажем некоторые результаты из теории чисел, играющие важную роль в дальнейшем изложении.

Лемма 1. Если наибольший общий делитель чисел m1,m2,...,mr равен 1, то существует n0 такое, что любое натуральное число n n0 можно представить в виде линейной комбинации

n k1m1 ... krmr ,

где ki 0 при всех i 1,r .

Доказательство. Возьмем произвольное n и разделим его с остатком на

Обозначим Mi n :pii(n) 0 .

Если Ei - состояние неприводимой цепи Маркова с периодом d , то из

nd k1m1d ... krmrd .

Лемма 2. В введенных выше обозначениях получаем, что все достаточно большие числа вида nd принадлежат множеству Mi .

Доказательство. Верна следующая цепочка неравенств: pii nd pii k1m1d ... krmrd

pii k1m1d ... pii krmrd pii m1d k1 ... pii m1d kr 0.

Лемма доказана.

30