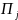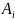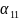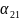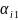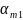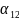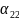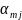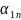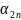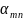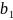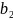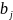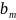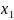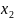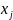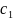Лекція 6 (1)
.docxЛекція 6 (1)
Основи лінійного програмування
Чому математичне програмування?
1959 р. – дата появи цього терміну. Назва пояснюється вибором програми дій (наших вчинків) для досягнення мети (розв’язання задачі). Бажано ціль досягати якнайшвидше – результат раціональних, цілеспрямованих дій або оптимальної програми дій: тут використовуються математичні методи розв’язання задач, знаходження extr функції на множинах з обмеженнями.
Традиційно вважається, що лінійне програмування (ЛП) є серцевина математичної підготовки економістів.
Зауваження! Слушно прийняти до уваги, що дане твердження з’явилося в епоху домінування теорії рівноважного стану.
Постановка задачі ЛП: економічний зміст, її математична модель (ММ)
а) Вербальне формулювання задачі ЛП
На
випуск n
видів продукції П₁,
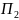 ,
…
,
…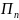 витрачається m
m
видів ресурсів (сировина, матеріали,
трудові ресурси тощо) А₁,
витрачається m
m
видів ресурсів (сировина, матеріали,
трудові ресурси тощо) А₁,
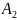 ,…
,…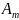 .
.
Відомі
витрати
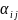 ресурсів і-го виду на одиницю продукції
j-го
виду, обсяг
ресурсів і-го виду на одиницю продукції
j-го
виду, обсяг
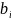 ресурсів і-го виду та величина прибутку
ресурсів і-го виду та величина прибутку
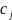 від
реалізації одиниці продукції j-го
виду. Треба так організувати випуск
продукції, виходячи із наявних ресурсів,
щоб одержувати найбільший прибуток.
від
реалізації одиниці продукції j-го
виду. Треба так організувати випуск
продукції, виходячи із наявних ресурсів,
щоб одержувати найбільший прибуток.
Словесно формулювання задачі відображено в таблиці та оцінка ресурсів наводиться в таблиці.
б) Табличний спосіб запису задачі ЛП
Види ресурсів |
Види продукції |
Запаси ресурсів |
|||||
П₁ |
|
|
|
|
|
||
А₁
-
-
|
-
-
|
-
-
|
- - - - - - |
-
-
|
- - - - - - |
-
-
|
-
-
|
Випуск продукції |
|
|
- |
|
- |
|
|
Прибуток від одиниці продукції |
|
|
- |
|
- |
|
|
Від табличного способу подання інформації перейдемо до аналітичного, тобто запишемо рівняння ММ.
Змінні
х₁,
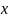 ,
…
– кількість одиниць випущеної продукції
відповідно П₁,
,
…
,
…
– кількість одиниць випущеної продукції
відповідно П₁,
,
…
в) Аналітичний запис задачі ЛП
Фактичні витрати відповідного виду не можуть перевищувати наявний їх обсяг (*)
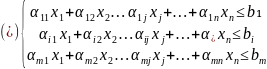
(**)Із
економічного змісту:
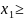 0,
0,
 0,
…
0,
…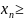 0.
Прибуток складає від випуску всієї
продукції
0.
Прибуток складає від випуску всієї
продукції (***)ᵶ=
(***)ᵶ=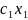 +
+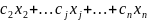 →max,
зрозуміло.
→max,
зрозуміло.
Система нерівностей (*) і (**) та лінійна форма (***) або функція мети, цільова функція визначає ММ задачі.
Від координатної розгорнутої форми запису задачі лінійного програмування (ЗЛП) перейдемо до компактної матричної
 →
extr
(max або
min)
→
extr
(max або
min)
 (i=1,
2,…,m)
(i=1,
2,…,m)
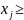 0
(j=1,2,…,n)
0
(j=1,2,…,n)
загальноприйнятої у літературі.
Форми запису задачі ЛП
Існують три: загальна
→ extr (max або min)
(i=1,
2,…, )
)
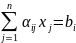 (i=
(i=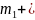 1,…,m)
1,…,m)
0 (j=1,2,…,n),
яка зручна для теоретичних досліджень;
Стандартна
→ extr
(i=1, 2,…,m)
0 (j=1,2,…,n),
до якої зводяться більшість задач практики;
Канонічна
→ extr
(i=1, 2,…,m)
0 (j=1,2,…,n),
яка використовується при чисельному розв’язанні задач ЛП.
Чим відрізняються наведені вище форми запису задачі ЛП?
Загальна
передбачає мішану сукупність рівнянь
і нерівностей; стандартна
– тільки нерівностей одного сенсу (в
одну сторону); канонічна
– тільки
рівності, зберігаючи умову
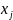 >=0
.
>=0
.
!Як здійснюється перехід від стандартної форми канонічної?
від
«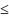 »
перехід до «=» через + додаткові змінні
»
перехід до «=» через + додаткові змінні
від
«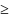 »
перехід до «=» через – додаткові змінні
»
перехід до «=» через – додаткові змінні
Різновиди запису канонічної форми задачі ЛП
Система обмежень переписується у векторному вигляді
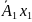 +
+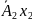 +…+
+…+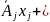 …
…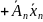 =
=
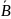 ,
,
де
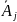 =
=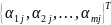 є вектор
стовпець умов
затрат, Т-індекс транспортування;
є вектор
стовпець умов
затрат, Т-індекс транспортування;
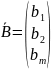 є
вектор обмежень (запасів).
є
вектор обмежень (запасів).
!Тоді вектор обмежень є розвинення в базисі векторів затрат, – коефіцієнти розвинення.
Задача
ЛП формулюється:
знайти точки
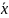 =(
=(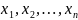 )
з невід’ємними
координатами
0
такі, що виконується
)
з невід’ємними
координатами
0
такі, що виконується
+…+
…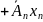 =
,
=
,
причому
лінійна форма ᵶ≡f(x)=c₁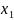 +…+
+…+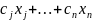 досягає
екстремуму extr
(max
f
або
min
f).
досягає
екстремуму extr
(max
f
або
min
f).
Канонічна
форма задачі ЛП з
використанням матрично-векторного
запису формулюється: знайти ᵶ max
(min)=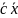 при умові А
=
,
де
при умові А
=
,
де
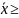 0,
причому
0,
причому
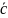 =
=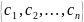 є вектор-строка;
=
є вектор-строка;
=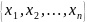 є вектор-стовпець; А= (
є вектор-стовпець; А= (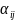 ),
i=1,
2,…,m;
j=1,2,…,n
є матриця системи обмежень;
),
i=1,
2,…,m;
j=1,2,…,n
є матриця системи обмежень;
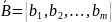 – вектор стовпець обмежень;
– вектор стовпець обмежень;
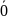 – нуль-вектор.
– нуль-вектор.
Термінологія
Обмеження (i=
 )
в економіці називаються лімітами.
)
в економіці називаються лімітами.Набір
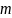 змінних таких, що матриця, складена із
коефіцієнтів біля цих змінних буде
невироджена (det
A
≠ 0), утворює
базис;
самі змінні називаються базисними.
змінних таких, що матриця, складена із
коефіцієнтів біля цих змінних буде
невироджена (det
A
≠ 0), утворює
базис;
самі змінні називаються базисними.Розв’язки з невід’ємними значеннями змінних, тобто
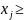 0,
будуть допустимими.
0,
будуть допустимими.
Геометрично базисні розв’язки є вершини многогранника умов – області М задачі ЛП (випадок 2-ох змінних).
Оптимальним розв’язком задачі ЛП називається сукупність чисел {х1, х2, …, хn}, що задовольняє умовам задачі і лінійна форма досягає екстремуму.
Для економістів розв’язок = план.
План
називається базисним, якщо вектори
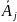 розвинення
розвинення
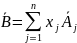 для
для
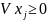 являються
лінійно незалежними.
являються
лінійно незалежними.
Кожен план відповідає деякій точці ОДЗ (многогранника умов). Плани, що відповідають вершинам ОДЗ називаються опорними.
Геометричне (графічне) розв’язання ЗЛП
В окремому випадку двовимірного простору економічних подій (розглядаються лише два економічних фактори) ММ задачі ЛП записується і формується так: знайти вектор-план Х={x1, x2} що задовольняє обмеженням – системі нерівностей
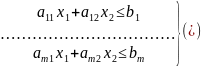 ,
,
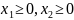 і
надає екстремального (extr)
значення (мінімального min
або
максимального
max)
лінійній функції
і
надає екстремального (extr)
значення (мінімального min
або
максимального
max)
лінійній функції
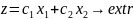 –
цільовій або функції мети (лінія
рівня).
–
цільовій або функції мети (лінія
рівня).
Зауваження. У випадку рівності кожне відношення для обмеження (*) є пряма на координатній площині.
Кожна
пряма L:
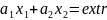 розділяє координатну площину на дві
напівплощини – додатну та від’ємну:
відповідно всі точки >
розділяє координатну площину на дві
напівплощини – додатну та від’ємну:
відповідно всі точки > V
точки < b
(під прямою). Вектор
нормалі
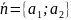 вказує
на це.
вказує
на це.

Нагадаємо знаки квадратичної координатної площини х1Ох2 – простору економічних подій.
Вектор нормалі (або grad z – градієнт) лінійної функції вказує напрямок її зростання.
Область допустимих значень (ОДЗ) визначається системою нерівностей (*): завжди розташована у 1-му квадранті і може бути многогранником замкненим або відкритою областю М.
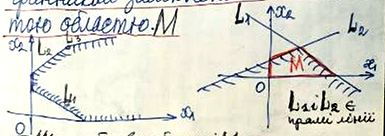
Щодо побудови області М
Перетин напівплощин, визначуваних нерівностями системи обмежень, може давати:

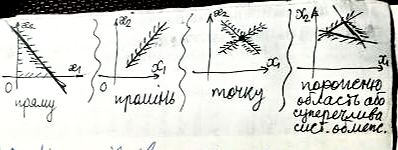
Лінія
рівнів
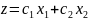 є пряма
є пряма
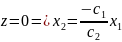 ,
що проходить через початок координат
і пересовується паралельно самій собі
в напрямку grad
z.
,
що проходить через початок координат
і пересовується паралельно самій собі
в напрямку grad
z.
Геометричне формулювання задачі ЛП: серед всіх точок обл. М відшукати таку, щоб лінія рівнів z (функція мети) приймала: найменше значення (zmin) – це 1-а М; найбільше значення (zmax) – остання точка зустрічі за умови паралельного переносу лінії нульового рівня z0 самій собі в бік grad z.
Взаємне розташування області допустимих розв’язків (ОДЗ) і лінії рівнів (z0)

Нескінченна множина розв’язків або альтернативний оптимум (min).

Приклад
1.
Знайти max
цільової функції
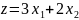 для системи обмежень:
для системи обмежень:
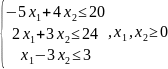
Крок 1. Будується ОДЗ:
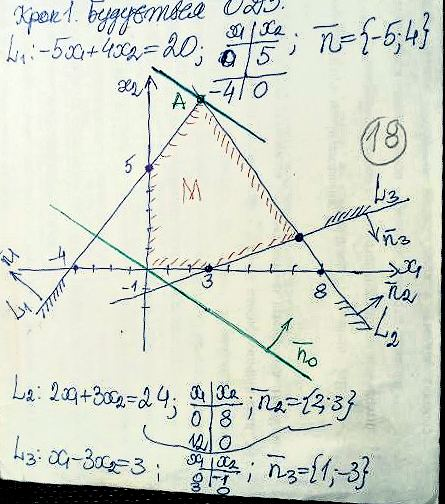
Крок
2.
Будується лінія нульового рівня:
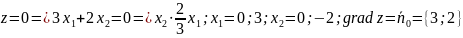
Вона пересувається || самій собі в напрямку grad z. Остання точка перетину лінії рівня з областю М відповідає zmax.
Крок 3.
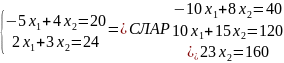
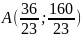
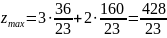
Інший спосіб розв’язання. Обчислити: координати усіх вершин многогранника; значення z у вершинах області М; вибрати найбільше числове значення.
Короткий зміст теорії ЛП
Лема1. Множина розв’язків системи обмежень задачі ЛП опукла.
 Опуклим
тілом називається таке, якому разом з
довільними його точками належить і весь
відрізок, що з’єднує
ці точки.
Опуклим
тілом називається таке, якому разом з
довільними його точками належить і весь
відрізок, що з’єднує
ці точки.


 Приклади:
круг; еліпс; ; ; паралелепіпед; площина
є випукла фігура ( область)
Приклади:
круг; еліпс; ; ; паралелепіпед; площина
є випукла фігура ( область)
 не є випуклою.
не є випуклою.
Лема2. Перетин 2-ох опуклих множин є опукла множина.
Лема3. Множина планів задачі ЛП опукла.
Теорема 1. Випукла лінійна комбінація кутових точок випуклого обмеженого многогранника умов (конуса К) не виходть за нього.
Приклад:

Вектори
λ₁,
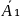 +
+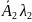 =
=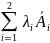 утворюють лінійну комбінацію і лежать
в куту, який називається конусом К.
утворюють лінійну комбінацію і лежать
в куту, який називається конусом К.
При
умові λ₁+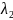 =1
буде випукла лінійна комбінація, причому
λ₁=
λ,
=1-λ
і λє(0,1): множині всіх випуклих комбінацій
векторів
=1
буде випукла лінійна комбінація, причому
λ₁=
λ,
=1-λ
і λє(0,1): множині всіх випуклих комбінацій
векторів
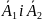 відповідає прямолінійний відрізок
кінців цих векторів.
відповідає прямолінійний відрізок
кінців цих векторів.
Якщо такими є вершини многогранника, то згадуваному відрізку відповідає ребро.
Теорема 2. Extr лінійної форми досягається в кутовій точці конуса К.
Теорема
3. Якщо
існує множина лінійно незалежних
векторів
...
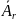 таких,
що виконується х₁
таких,
що виконується х₁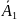 +…+
+…+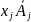 +…+
+…+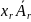 =
=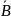
Для
Ʉ
0
(j=1,2…r),
то
точка
=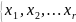 ;
0, 0,…0} є кутова для випуклої множини К
розв’язків
системи обмежень задачі ЛП.
;
0, 0,…0} є кутова для випуклої множини К
розв’язків
системи обмежень задачі ЛП.
Теорема
4. (обернена
до теор.3). Якщо
=
;
0, 0,…0} кутова точка множини К, то існують
лінійно незалежні вектори
...
такі, що має місце
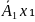 +…+
+…+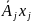 +…+
+…+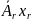 =
для
0
(j=1,2…r)
=
для
0
(j=1,2…r)