
Лекція 3
.docxЛекція №3
Основні припущення для простої лінійної регресії
Логіка подальших подій: є економетрична модель – інструмент моделювання. Слід окреслити умови, коли застосування його найменше.
По-іншому, наскільки вдало емпіричні коефіцієнти b0 та b1 відповідають β0 та β1?
Припущення
щодо
 є
головним для інтерпретації
регресійних оцінок
математичного сподівання (умови
Гаусса-Маркова).
є
головним для інтерпретації
регресійних оцінок
математичного сподівання (умови
Гаусса-Маркова).
 фактори,
що враховані моделлю (віднесені до
фактори,
що враховані моделлю (віднесені до
 )
систематично не впливають:
)
систематично не впливають:
 нейтралізують
нейтралізують
 .
.

ВВ незалежні між собою (їх коеф. кореляції = 0):


Гомоскедастичність (однакова дисперсія ВВ )
Гетероскедастичність
(нерівна дисперсія)


Незалежність між значеннями
 (нульова
коваріація між ними)
(нульова
коваріація між ними)Регресійну модель визначено (специфіковано) правильно.

ВВ ε розподілена нормально з математичним сподіванням = 0 та сталою дисперсією
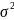 ,
тобто
,
тобто

При виконанні вказаних припущень оцінки, отримані МНК, володіють властивостями:
Незміщені, тобто
 ,
тому що
,
тому що
 :
відсутність систематичної похибки у
визначенні розташування лінії регресії.
:
відсутність систематичної похибки у
визначенні розташування лінії регресії.Оцінки переконливі (обґрунтовані):
 .
По-іншому,
збільшення об’єму вибірки сприяє
підвищенню надійності оцінок.
.
По-іншому,
збільшення об’єму вибірки сприяє
підвищенню надійності оцінок.
Пояснювальні змінні не є ВВ; число спостережень >> числа пояснювальних змінних.
Оцінки ефективні: мають найменшу дисперсію.
BLUE – найкращі лінійні незміщені оцінки (це є теорема Гаусса-Маркова).
Мають місце робочі формули:

де
співмножник
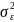 ,
будучи оцінкою дисперсії випадкової
величини ε,
замінюється на величину
,
будучи оцінкою дисперсії випадкової
величини ε,
замінюється на величину
 ,
яка обчислюється:
,
яка обчислюється:
 ,
,
причому
величина
 є непояснювана дисперсія, міра відхилення
залежної змінної навколо лінії регресії;
n
– об’єм вибірки; цифра 2 відповідає
кількості оцінюваних параметрів моделі.
є непояснювана дисперсія, міра відхилення
залежної змінної навколо лінії регресії;
n
– об’єм вибірки; цифра 2 відповідає
кількості оцінюваних параметрів моделі.

Величина
 називається
стандартною
похибкою оцінки
(стандартна
похибки регресії).
називається
стандартною
похибкою оцінки
(стандартна
похибки регресії).
Величини

Є стандартні похибки коеф. регресії.
Геометричні пояснення формул коеф.
 визначає
нахил прямої регресії. Чим більше
розкиданість значень Y
навколо лінії регресії, тим (в середньому)
більша похибка в обчисленні нахилу
прямої.
визначає
нахил прямої регресії. Чим більше
розкиданість значень Y
навколо лінії регресії, тим (в середньому)
більша похибка в обчисленні нахилу
прямої.

Точки
належать прямій регресії,

 :
розкиданості нема.
:
розкиданості нема.
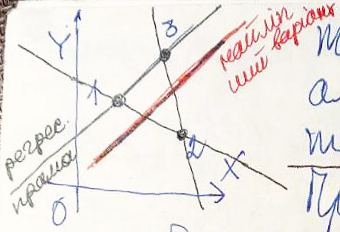
Та ж пряма регресії, але точки не належать їй – суттєва розкиданість.
При
виключенні з розгляду будь-якої точки
прямі регресії суттєво відрізняються
між собою: зовсім різні кути нахилу цих
прямих. Отже, стандартна похибка
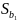 коеф.
регресії b1
буде
значною.
коеф.
регресії b1
буде
значною.
Для великих по модулю значеннях Х навіть незначна зміна нахилу регресійної прямої призводить до значної зміни оцінки вільного члена, бо в середньому велика віддаль від точок спостереження до осі oY.

Інтервальні оцінки коеф. лінійного рівняння регресії
Припускається, що ВВ коеф. b0 та b1 мають нормальні розподіли.
Розраховується t-статистика для кожного параметра

Вони мають розподіл Стьюдента з числом ступенів вільності v = n – 2.
Рівень
значущості
 для визначення 100(1-α)% довірчого інтервалу
за допомогою таблиць критичних точок
розподілу Стьюдента та довірчою
ймовірністю
для визначення 100(1-α)% довірчого інтервалу
за допомогою таблиць критичних точок
розподілу Стьюдента та довірчою
ймовірністю
 і числом ступенів вільності v
= n
– 2 визначається
критичні значення
і числом ступенів вільності v
= n
– 2 визначається
критичні значення
 ,
що
задовольняє умові
,
що
задовольняє умові

Підставляючи кожну статистику в цей результат, маємо:


Після перетворень виразів в дужках одержуємо:

Далі користуються виразами для S(b0) та S(b1).
Отже, довірчі інтервали:


З надійністю (1 – α) покривають параметри β0 та β1. Фактично, довірчий інтервал визначає значення теоретичних коефіцієнтів регресії β₀ та β₁, які будуть придатні з надійністю (1-α) при знайдених оцінках b₀ та b₁.
Довірчі інтервали залежної змінної
Центральне питання – прогнозування значень залежної змінної при певних значеннях пояснювальних змінних.
Передбачення середнього значення
Довірчий
інтервал для М (Y│Х= )=
β₀+β₁
має вигляд:
)=
β₀+β₁
має вигляд:
[
b₀+b₁
- ;n-2·
;n-2·
 ;
;
b₀+b₁ + ;n-2· ]
Для перевірки гіпотез:
нульвої
Н₀:
М (Y│Х=
)= ;
;
 альтернативної
Н₁:
М (Y│Х=
)
=
;
альтернативної
Н₁:
М (Y│Х=
)
=
;
Передбачення індивідуальних значень залежної змінної
Важливіше знати дисперсію Y, ніж її середні значення або довірчі інтервали для умовного математичного сподівання
ВВ

Має розподіл Стьюдента з V=n-2.
Отже,
P[
-
;n-2
<
 <
;n-2]=1-α.
<
;n-2]=1-α.
Таким
чином, інтервал [b₀+b₁
±
;n-2·
 ]
визначає межі, за якими може бути не
більше 100*α% точок спостережень при Х=
.
Цей інтервал ширший за попередній (
довірчий інтервал умовного сподівання).
]
визначає межі, за якими може бути не
більше 100*α% точок спостережень при Х=
.
Цей інтервал ширший за попередній (
довірчий інтервал умовного сподівання).
Перевірка лінійної регресійної моделі на адекватність здійснюється за F-критерієм Фішера і включає кроки:
Розраховується F-відношення
F₁,
n-2= ,
де індекси 1, (
,
де індекси 1, ( )
– ступені вільності.
)
– ступені вільності.
Вказується рівень значущості α, як правило α=0,05
За статистичними таблицями F-розподілу Фішера для ступенів вільності 1, ( ) та рівня значимості 2 знаходиться Fкр.
Якщо F > Fкр, то нульова гіпотеза Н₀, що β₁=0, відкидається з ризиком в 5%. Іншими словами, для нерівності F > Fкр побудована регресійна модель адекватна реальній дійсності.
Схема Стьюдента для перевірки значущості коефіцієнтів парної лінійної регресії
Будується t-статистика для кожного:
t= t=
t=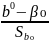 ,
де β₀,
β₁
–
теоретичні значення (гіпотетичні).
,
де β₀,
β₁
–
теоретичні значення (гіпотетичні).
В економетриці поширено:
нуль-гіпотеза Н₀: βᵢ=0, де і=0,1.
 Альтернативна
Н₁:
βᵢ
= 0.
Альтернативна
Н₁:
βᵢ
= 0.
Тоді
t-статистика
для параметрів набуває вигляду t= .
.
Вона
порівнюється з
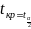 ;
(n-2).
;
(n-2).
Якщо
виконується │t│<
 <=> -
<
t
<
,
то
з ймовірністю (1-α) оцінка bᵢ
є статистично незначимою (приймається
нуль-гіпотеза)
<=> -
<
t
<
,
то
з ймовірністю (1-α) оцінка bᵢ
є статистично незначимою (приймається
нуль-гіпотеза)
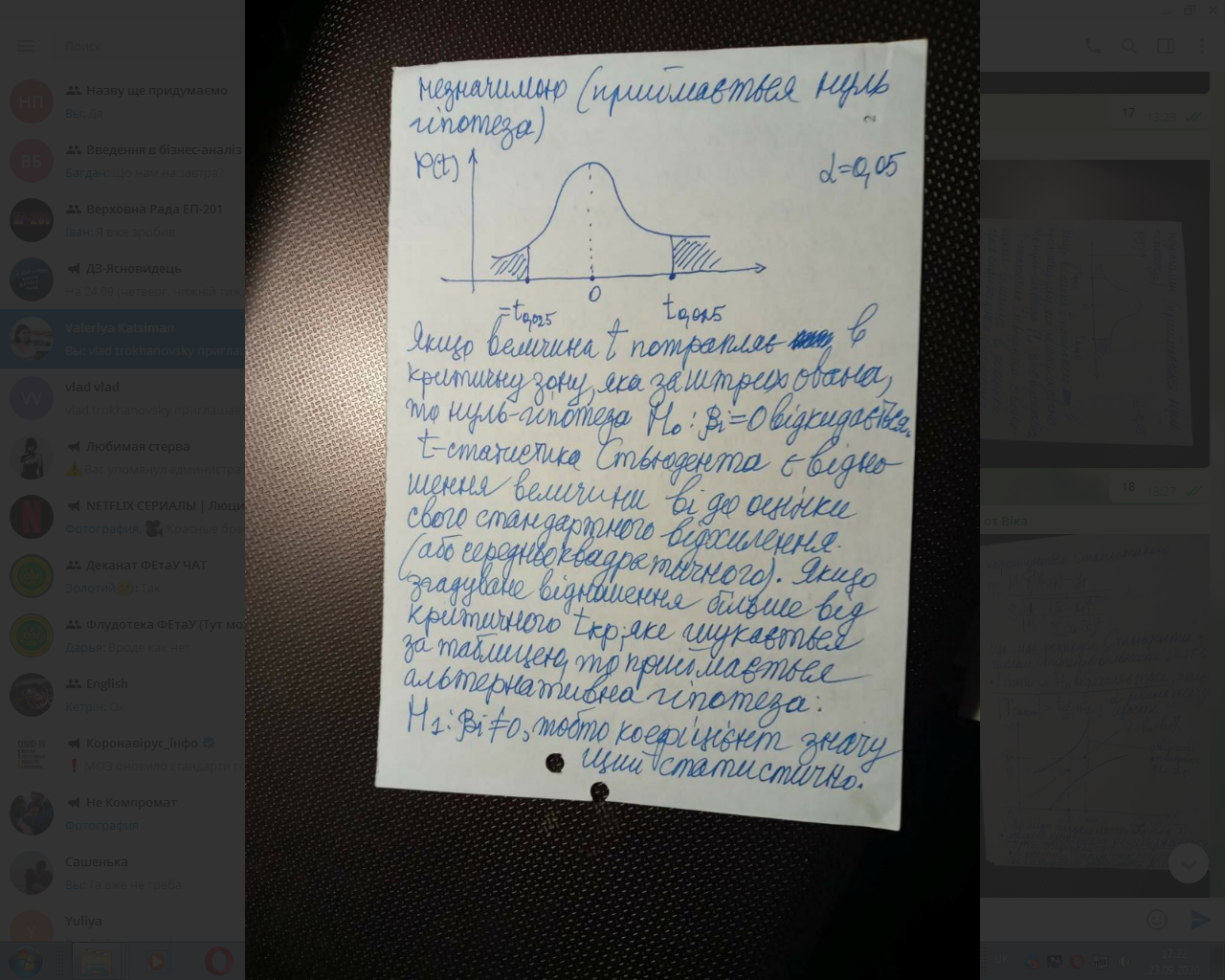
Якщо величина t потрапляє в критичну зону, яка заштрихована, то нуль-гіпотеза Н₀: βᵢ=0 відкидається.
t-статистика Стьюдента є відношення величини bᵢ до оцінки свого стандартного відхилення (або середньоквадратичного). Якщо згадуване відношення більше від критичного , яке шукається за таблицею, то приймається альтернативна гіпотеза: Н₁: βᵢ = 0, тобто коефіцієнт значущий статистично.
Користуються статистикою
T=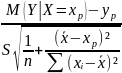 ,
що
має розподіл Стьюдента з числом ступенів
вільності V=n-2.
,
що
має розподіл Стьюдента з числом ступенів
вільності V=n-2.
Гіпотеза
Н₀
відхиляється
якщо
2-рівень
значущості. │ │>
;n-2;
│>
;n-2;
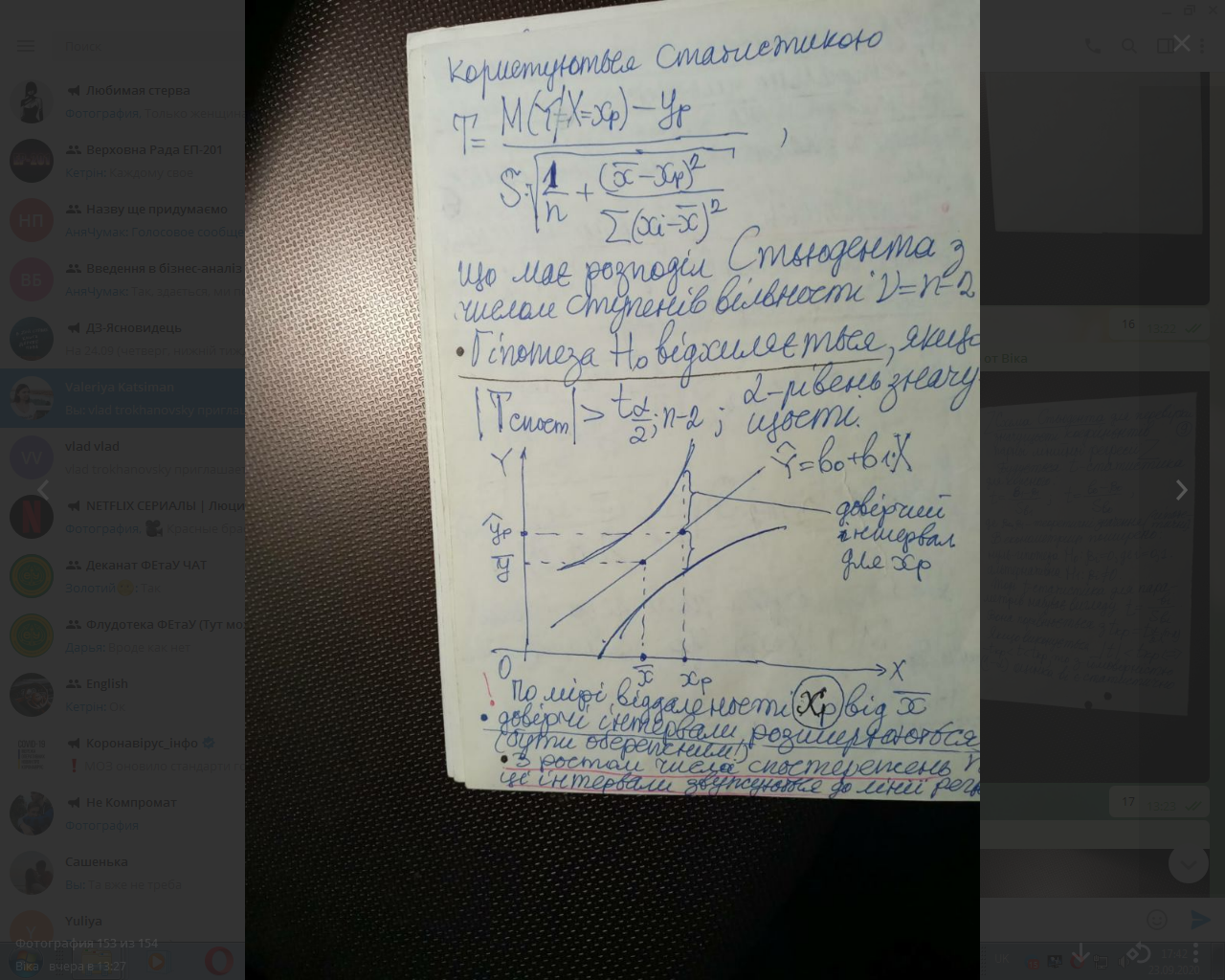
По
мірі віддаленості
від
 довірчі інтервали розширюються (бути
обережним!).
довірчі інтервали розширюються (бути
обережним!).
З ростом числа спостережень ці інтервали звужуються до лінії регресії.
