посібник зно математика

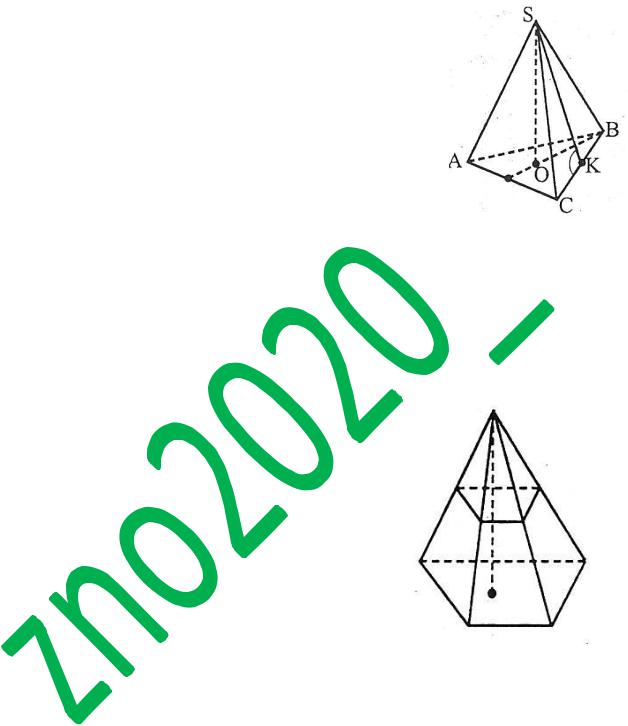
Наприклад: правильна трикутна піраміда SABC, 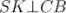, SK – апофема.

Управильній піраміді:

бічні ребра рівні;

бічні грані рівні;

апофеми рівні;

двогранні кути при основі рівні;

двогранні кути при бічних ребрах рівні;

кожна точка висоти правильної піраміди рівновіддалена від усіх вершин основи;

кожна точка висоти правильної піраміди рівновіддалена від усіх бічних граней;

кожна точка висоти правильної піраміди рівновіддалена від усіх бічних ребер.

Діагональним перерізом піраміди називається переріз площиною, яка проходить через два бічних ребра піраміди, що не належать одній грані.

Властивості паралельних перерізів пірамід

Теорема. Якщо піраміда перерізається площиною, паралельною основі, то:

1.бічні ребра та висота піраміди діляться цією площиною на пропорційні частини;

2.переріз – многокутник, подібний основі;

3.площі перерізу та основи відносяться як квадрати їх відстаней від вершини піраміди.

Якщо довільну n-кутну піраміду перерізати площиною, паралельною основі, то ця площина відітне від піраміди многогранник, дві грані якого подібні n- кутники, а інші n граней – трапеції. Цей многогранник називається зрізаною пірамідою.

Паралельні грані зрізаної піраміди називаються основами, а всі інші – бічними. Висотою зрізаної піраміди називається перпендикуляр, проведений з будь-якої точки однієї основи на площину іншої основи.

Зрізана піраміда називається правильною, якщо вона складає частину правильної піраміди. Висота бічної грані правильної зрізаної піраміди, проведена до ребра основи, називається апофемою.

Управильній зрізаній піраміді:

бічні ребра рівні;

бічні грані рівні;

апофеми рівні;

двогранні кути при кожній основі рівні;

двогранні кути при бічних ребрах рівні;

кожна точка прямої, яка проходить через центри її основ, рівновіддалена від усіх вершин кожної основи, рівновіддалена від площини бічних граней, рівновіддалена від прямих, на яких лежать бічні ребра.

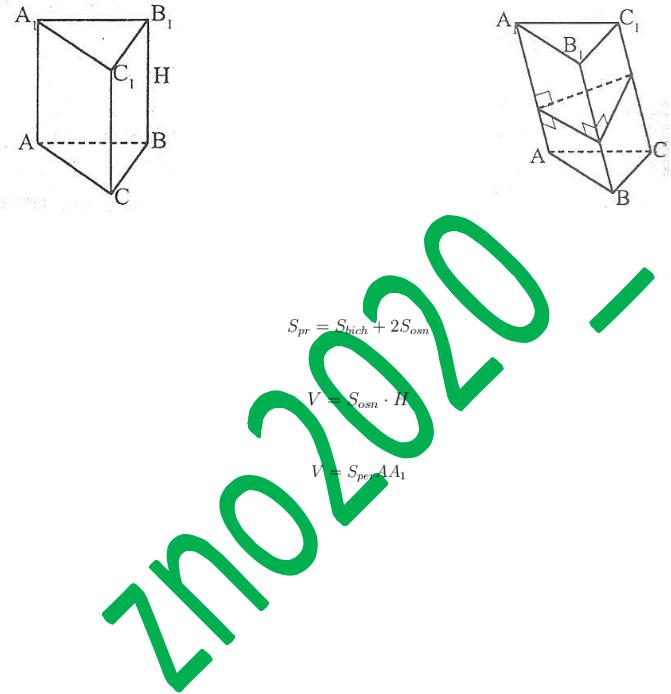
Формули площі поверхонь і об'ємів призми

Площею бічної поверхні призми є сума площ її бічних граней. Площею повної поверхні призми є

сума площ усіх її граней. Площа бічної поверхні прямої призми дорівнює добутку периметра основи на висоту призми, тобто на довжину бічного ребра.

Площу бічної поверхні призми можна обчислити за формулою:

,

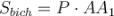де Р – периметр перпендикулярного перерізу (перерізу призми площиною, яка перпендикулярна до бічних ребер і перетинає всі її бічні ребра), АА1 – довжина бічного ребра.

Площа повної поверхні призми (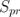) дорівнює сумі площі бічної поверхні (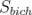) і площ двох основ (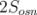

):

.

Об'єм V призми дорівнює добутку площі основи на висоту:

.

Об'єм V призми можна обчислити за формулою

,

де 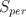— площа перпендикулярного перерізу, АА1—довжина бічного ребра.

Об'єм прямокутного паралелепіпеда дорівнює добутку його вимірів:

.

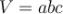Об'єм V куба дорівнює кубу його ребра:

.

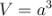Формули площі поверхонь і об'ємів піраміди

Площею повної поверхні піраміди є сума площ усіх її граней (тобто основи і бічних граней), а площею бічної поверхні піраміди — сума площ її бічних граней:

.

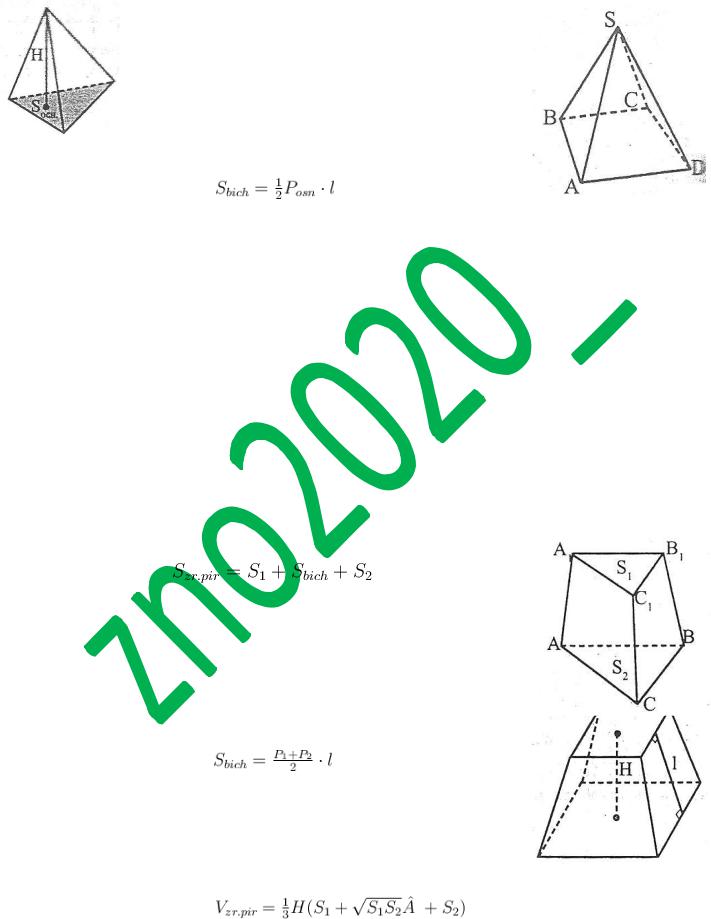
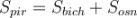Наприклад:

.

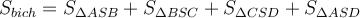Площа бічної поверхні правильної піраміди дорівнює половині добутку периметра основи на апофему:

де l – апофема.

Наприклад: .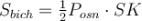

Якщо бічні грані піраміди нахилені до основи під кутом φ, а площа основи дорівнює 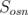, то площа бічної поверхні піраміди

.

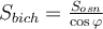Об’єм піраміди дорівнює третині добутку площі основи на висоту:

.

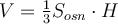Площа повної поверхні зрізаної піраміди дорівнює сумі площ усіх її граней (тобто основ і бічних граней), а

площа бічної поверхні зрізаної піраміди – сумі площ її бічних граней

.

Наприклад: 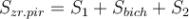, де

.

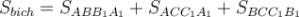Площа бічної поверхні правильної зрізаної піраміди дорівнює добутку півсуми периметрів основ на апофему.

,

де Р1, Р2 – периметри основ, l – апофема.

Об’єм V зрізаної піраміди, висота якої H, а площі основ дорівнюють S1 і S2, обчислюється за формулою:

.

Циліндри та їх властивості

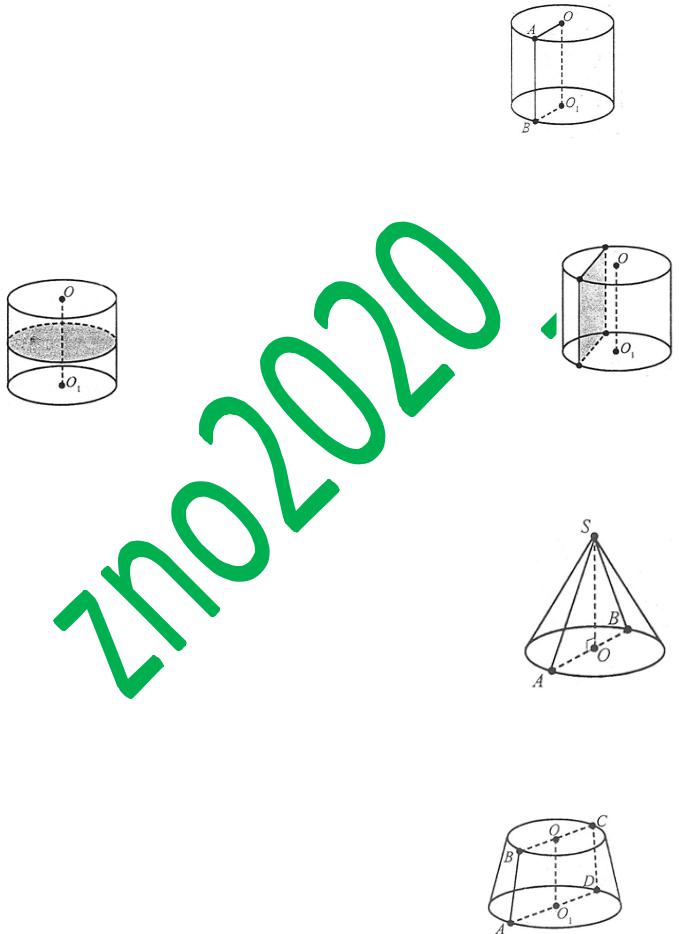
1. Циліндр

Циліндром називається тіло, утворене обертанням прямокутника навколо його сторони.

Наприклад: циліндр, утворений обертанням прямокутника ОАВО1 навколо ОО1,

ОО1 – вісь циліндра.

Сторони ОА і О1В описують рівні круги, які лежать у паралельних площинах і називаються основами циліндра. Радіуси кругів називаються радіусами циліндра. Сторона АВ описує поверхню, яка називається бічною поверхнею циліндра. Відрізки бічної поверхні, які паралельні і дорівнюють АВ, називаються твірними циліндра.

Висотою циліндра називається відрізок, перпендикулярний до основ, кінці якого належать основам. Висота циліндра дорівнює його твірній.

2. Перерізи циліндра

Переріз циліндра площиною, перпендикулярною до його осі, – круг, що дорівнює основі; а переріз площиною, паралельною осі, – прямокутник або відрізок.

Осьовий переріз – прямокутник зі сторонами, що дорівнюють висоті циліндра і діаметру його основи.

Примітка. Якщо точніше, то тіло, утворене обертанням прямокутника навколо його сторони називається прямим круговим циліндром. Саме такі циліндри

розглядають у шкільному курсі стереометрії і називають їх просто циліндрами. У широкому розумінні слова, циліндр – це тіло, яке складається з двох обмежених плоских областей, які можна сумістити паралельним перенесенням, і всіх відрізків, які з’єднують відповідні точки.

Конус.

Конусом називається тіло, утворене обертанням прямокутного трикутника навколо одного із катетів.

Якщо прямокутний трикутник SAO обертається навколо катета SO, то його гіпотенуза

SA, описує бічну поверхню, а катет ОА – круг – основу конуса.

Радіус цього круга називається радіусом конуса; точка S, відрізок SA, відрізок SO, пряма

SO називаються відповідно вершиною, твірною, висотою і віссю конуса.

2. Перерізи конуса.

Осьовий переріз конуса – переріз конуса площиною, яка проходить через його вісь. Усі осьові перерізи конуса є рівнобедреними трикутниками, рівними між собою.

Наприклад: – осьовий переріз (SA=SB).

Переріз конуса площиною, яка паралельна площині основи конуса, є круг.

Зрізаним конусом називається частина конуса, обмежена його основою і перерізом, паралельним площині основи.

Зрізаний конус можна одержати в результаті рівнобедреної трапеції навколо її осі симетрії або обертаючи прямокутну трапецію навколо осі, що збігається з бічною стороною трапеції, перпендикулярною до основ.

Осьовий переріз зрізаного конуса – рівнобічна трапеція.

Наприклад: ABDC – осьовий переріз.

Зрізаний конус обмежений двома кругами – його основами – і бічною поверхнею.

Відстань між основами – висота зрізаного конуса.

Наприклад: ОО1 – висота, АВ – твірна.

Примітка. Якщо точніше, то тіло, утворене обертанням прямокутного трикутника навколо одного із катетів, називається прямим круговим конусом. Саме такі конуси розглядають у шкільному курсі стереометрії і називають їх просто конусами. У широкому розумінні слова, конус – це тіло, утворене всіма відрізками, які з’єднують дану точку (вершину конуса) з точками деякої обмеженої плоскої фігури (основою конуса).

Сфера (куля)

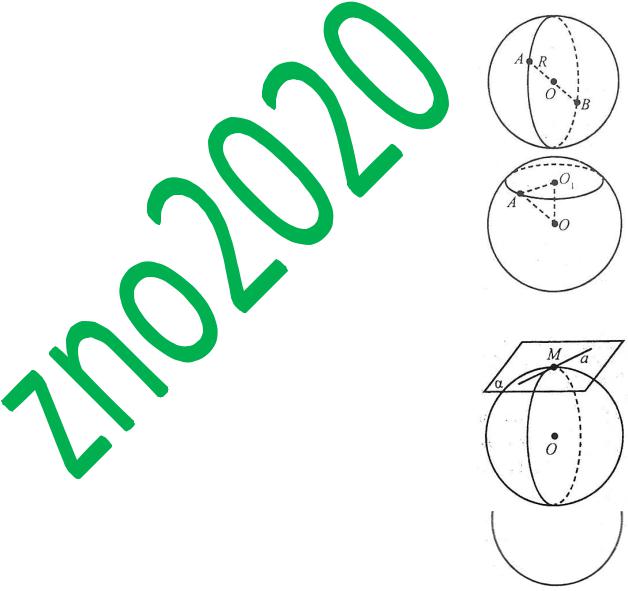
Сферою називається поверхня, яка складається з усіх точок простору, що знаходяться на даній відстані (яка називається радіусом) від даної точки (яка називається центром). Відрізок, який з’єднує дві точки сфери і проходить через її центр називають діаметром сфери.

Наприклад: О – центр сфери, ОА – радіус сфери, АВ – діаметр сфери.

Сферу можна отримати в результаті обертання кола навколо його діаметра.

Кулею називається тіло, утворене з усіх точок простору, що знаходяться на відстані, не більшій за дану (яка називається радіусом) від даної точки (яка називається центром). Кулю можна отримати в результаті обертання круга навколо його діаметра.

Будь-який переріз кулі площиною є круг, а переріз сфери площиною є коло.

Центр круга (кола) – основа перпендикуляра, опущеного із центра кулі (сфери) на січну площину. Переріз, який проходить через центр кулі (сфери), називається великим кругом

(колом).

Площина (пряма), яка має з кулею (сферою) тільки одну спільну точку, називається

дотичною площиною (прямою).

Дотична площина (пряма) перпендикулярна до радіуса кулі (сфери), проведеного в точку дотику. Якщо площина (пряма) проходить через точку сфери і перпендикулярна до радіуса, проведеного в цю точку, то вона дотикається до сфери.

2. Кульовий сегмент

Кульовим сегментом називають тіло, відтяте від кулі січною площиною.

Кульовий сегмент обмежений кругом, який називають основою, і сферичним сегментом. Відрізок діаметра, перпендикулярного до основи кульового (сферичного) сегмента, що міститься між основою і сферою, називають висотою кульового (сферичного) сегмента.

Координати вектора. Довжина вектора

1. Координати вектора

Координати вектора 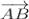, що має початок в точці А і кінець в точці В, дорівнюють різниці відповідних координат точок В і А.

Координати вектора у просторі

Якщо початком вектора є точка А(хА;уА;zA), а кінцем – точка В(хВ;уВ;zB), то

2. Довжина вектора

Довжина вектора (абсолютна величина, або модуль) – довжина відрізка, що зображує вектор. Позначення: .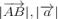

Довжина вектора у просторі

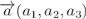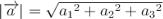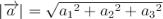Якщо є вектор, то = , де 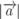– модуль вектора, 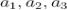– його координати.

Одиничним називається вектор 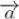, у якого .

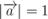Нульовим називається вектор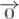 \, у якого початок і кінець збігаються. Нульовий вектор не має визначеного напрямку, а його модуль дорівнює нулю.

Задача 1. Знайдіть координати і довжини векторів 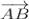і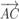 , якщо А(2;-3;-1), В(-4;-8;5), С(3;1;-2).

Розв’язання

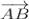( - 4 - 2; - 8 - ( - 3);5 - ( - 1)) = 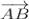( - 6; - 5;6)\];

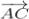(3 - 2;1 - ( - 3); - 2 - ( - 1)) = (1;4; - 1)\];

= ;

= .

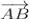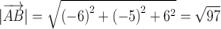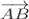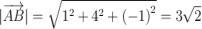Відповідь: , ,\, .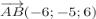

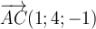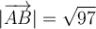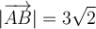Рівність векторів у просторі

Дії з векторами у просторі

Для трьох векторів (ОА, ОС і ОО1), які не лежать в одній площині й мають спільний початком (О), їхня сума зображується діагоналлю паралелепіпеда (ОВ1), побудованого на цих векторах, причому початок вектора-суми збігається з початком цих векторів.

Координати вектора-суми векторів дорівнюють сумі відповідних координат даних векторів.

Сума векторів у просторі

Різниця векторів у просторі

Множення вектора на число у просторі

Задача 2. Задано вектори .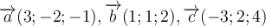

Знайдіть координати векторів .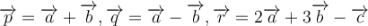

Розв’язання

;

;

Відповідь: .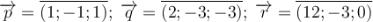

Колінеарність векторів у просторі

Якщо є вектори 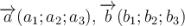і вони колінеарні, то .

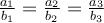Якщо є вектори 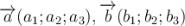, то 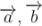– колінеарні вектори.

Задача 3. Знайдіть значення m і n, при яких вектори 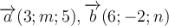колінеарні.

Розв’язання

У колінеарних векторів координати пропорційні, звідси 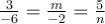. Маємо два рівняння:

1) ;

2) .

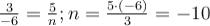Відповідь: m=1, n=-10.

Скалярний добуток двох векторів

Скалярним добутком двох векторів називається число, яке дорівнює сумі добутків відповідних координат цих векторів. Позначення таке саме, як і для добутку чисел, – .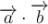

Скалярний добуток двох векторів на площині

Якщо є вектори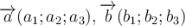 , то .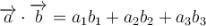

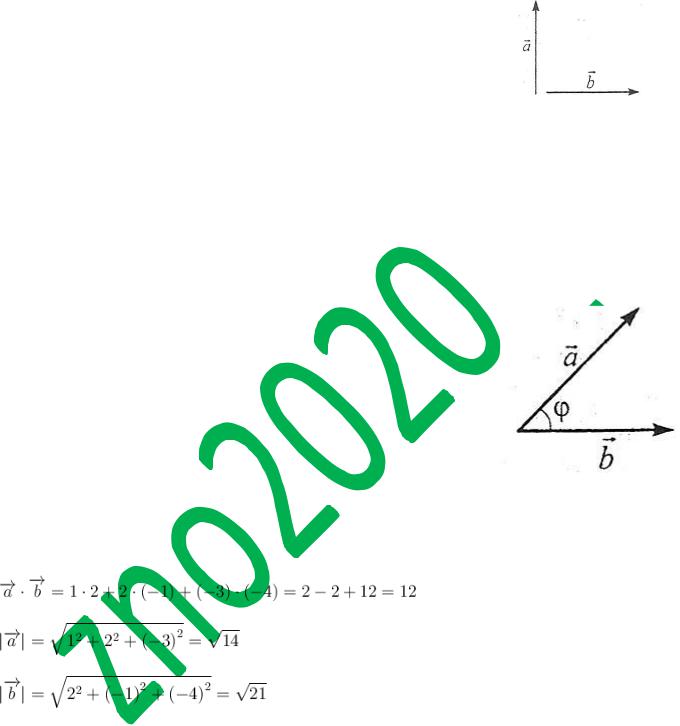
Теорема. Скалярний добуток двох векторів дорівнює добутку довжин цих векторів на косинус кута між ними.

Отже, .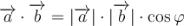

Задача 4. Знайдіть кут між векторами і .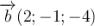

Розв’язання

Скористаємося формулою

,

;

;

;

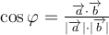тоді .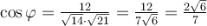

Звідси .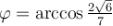

Ознака перпендикулярності векторів

Якщо вектори перпендикулярні, то їхній скалярний добуток дорівнює нулю.

І навпаки, якщо скалярний добуток відмінних від нуля векторів дорівнює нулю, то вектори перпендикулярні.