
6семестр / ТАУ_ТР
.pdf
Типовой расчет по курсу «Теория автоматического управления»
на тему
«Анализ нелинейных систем автоматического управления»
Исходные данные
Исходными данными для исследования нелинейной системы релейного типа являются структурная схема системы, представленная на Рис. 1.1, и вид нелинейного элемента с известными параметрами, представленный на Рис. 1.2.
Рис. 1.1. – Исходная структурная схема нелинейной системы.
Рис. 1.2. – Нелинейный элемент типа 3 – двухпозиционное реле с гистерезисом.
В рамках настоящей работы исследуется система при отсутствии входного воздействия, то есть f(t)=0.
Передаточные функции исходной системы заданы следующего вида:
W1(p) = k1 ; |
(1.1) |
; |
(1.2) |
W3(p) = pT0 ; |
(1.3) |
ϕ(y) – нелинейный элемент типа двухпозиционное реле с гистерезисом.
Здесь:
B = 2; c = 4;
k1 = 10;
k2 = 16; a = 8; b = 16; T0 = 1 c.
2

1. Исследование структуры фазового портрета нелинейной системы
Проведем структурные преобразования исходной схемы (Рис.1.1):
а) Объединим передаточные звенья W1(p) и W2(p) в звено W12(p). Поскольку они соединены последовательно, то их передаточные функции следует перемножить:
(2.1)
б) Ветвь со звеном W3(p) и единичную обратную связь объединим в эквивалентное звено W30(p) в соответствии с правилом параллельного соединения:
(2.2)
В результате получим структурную схему, представленную на Рис.2.1:
Рис. 2.1. – Приведенная структурная схема нелинейной системы.
Перейдем от операторной формы дифференциальных уравнений (2.1) и (2.2) к естественной форме с независимым аргументом t. После подстановки выражений передаточных функций для (2.1) и (2.2) получим:
|
(2.3) |
Y(p) = X(p)pT0 – X(p) |
(2.4) |
Подставляя в (2.3) и (2.4) значения параметров и переходя от изображений к оригиналам, получим дифференциальные уравнения следующего вида:
x″(t) + 8x′(t) + 16x(t) = 160z(t) |
(2.5) |
y(t) = x′(t) – x(t) |
(2.6) |
3

Уравнения (2.5) и (2.6) и уравнение нелинейного элемента
(2.7)
полностью описывают динамику системы.
Подставим выражение для z(t) из (2.5) и для y(t) из (2.6) в (2.7):
(2.8)
Врезультате получаются 2 дифференциальных уравнения, откуда следует, что на фазовой плоскости будут иметь место траектории двух типов. Неравенства указывают в какой области фазовой плоскости справедливы решения (интегральные кривые) того или иного уравнения.
Вкачестве координат фазовой плоскости примем переменные (x, v = x′). Тогда система (2.8) представится через фазовые переменные следующим образом:
(2.9)
Из неравенств (2.9) могут быть найдены полупрямые, являющиеся границами областей с различными типами фазовых траекторий.
|
(2.10) |
Определим первый тип фазовых траекторий, для этого подставим соответствующее |
|
значение z = 2 в уравнение (2.5) и запишем в следующем виде: |
|
x″(t) + 8x′(t) + 16(x(t) - 160×2/16) = 0 |
(2.11) |
4

Введем новую переменную:
(2.12)
Так как:
 ,
,
перепишем уравнение (2.11) следующим образом:
(2.13)
Для определения характера фазовых траекторий воспользуемся справочным материалом из методических указаний. Представим уравнение (2.13) в виде:
(2.14)
Находим, что ω0 = 4, d = 1. Таким образом, фазовые траектории соответствуют Рис. 2.2.
Рис. 2.2. - Изображение фазовых траекторий при ω0 > 0 и d = 1.
Из (2.12) следует, что:
Следовательно, фазовый портрет уравнения (2.11) будет отличаться от портрета (2.13) смещением всей картины по оси x на величину (+20).
Второй тип фазовых траекторий соответствует дифференциальному уравнению: x″(t) + 8x′(t) + 16(x(t) + 160×2/16) = 0 (2.15)
Следовательно, фазовый портрет уравнения (2.15) будет отличаться от портрета (2.13) смещением всей картины по оси x на величину (-20).
5

Качественный фазовый портрет нелинейной системы представлен на Рис.2.3. Из него следует, что точка v = x = 0 – особая точка.
Рис. 2.3. – Качественный фазовый портрет нелинейной системы.
2. Построение фазового портрета системы с помощью стандартного ППП MatLab
Зададим модель системы в ППП MatLab Simulink с реализацией передаточных функций в виде моделей пространства состояний. Для этого преобразуем исходную структурную схему (Рис.1.1) к виду Рис.2.4. При этом объединим звенья W2(p) и W3(p). В этом случае передаточная функция звена будет иметь вид:
 .
.
Таким образом получим структурную схему вида:
Рис. 2.4. - Преобразованная структурная схема исходной системы.
6

В результате можно задать передаточные функции  и
и  с помощью модели пространства состояний. Заданная модель системы в MatLab Simulink отображена на Рис.2.5.
с помощью модели пространства состояний. Заданная модель системы в MatLab Simulink отображена на Рис.2.5.
Рис. 2.5. – Модель нелинейной системы.
Для построения фазового портрета зададим три произвольных значения начальных условий (2, 2), (-2, 2), (32, 16) и отобразим полученные фазовые траектории – Рис.2.6.
Рис. 2.6. – Фазовые траектории системы.
Из Рис. 2.6 видно, что при всех начальных условиях возникают автоколебания. Как и в п.1 исследования точка с координатами (0, 0) соответствует точке равновесия типа «центр».
Особая точка устойчива по Ляпунову и асимптотически неустойчива, процессы в системе имеют периодический гармонический характер, устойчивы по Ляпунову и асимптотически неустойчивы.
7

Зададим еще три фазовые траектории и построим график изменения процесса x(t) для них: примем начальные условия (x01 = 1, x′01 = 0), (x02 = 0, x′02 = 4), (x03 = -8, x′03 = -8).
На Рис. 2.7 отображены построенные фазовые траектории, а на Рис.2.8-2.10 графики изменения процесса x(t) по каждому случаю.
Рис. 2.7. – Фазовые траектории системы.
Рис. 2.8. – График процесса x(t) при НУ (x01 = 1, x′01 = 0).
8
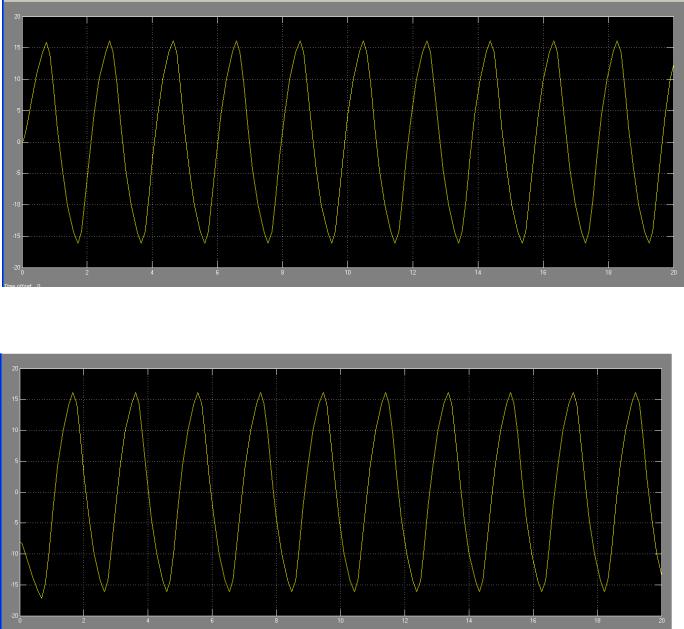
Рис. 2.9. – График процесса x(t) при НУ (x02 = 0, x′02 = 4).
Рис. 2.10. – График процесса x(t) при НУ (x03 = -8, x′03 = -8).
Как видно из Рис.2.8 - 2.10 при указанных начальных условиях в системе устанавливаются автоколебания, являющиеся устойчивыми. Период автоколебаний 2 с, амплитуда 16,3.
9

3. Исследование влияния ширины петли гистерезиса на возникновение автоколебаний в системе
Для исследования данного вопроса заменим исходный нелинейный элемент 3 (двухпозиционное реле с гистерезисом) на нелинейный элемент 4 (трехпозиционное реле с гистерезисом), изображенный на Рис. 3.1. Значение параметра с = 4 остается неизменным, значение параметра h принимаем равным 10 (значение из ближайшего варианта задания с нелинейным элементов вида 4, при котором соблюдается h > c).
|
z |
|
|
+ B |
|
−h |
−c |
y |
|
+c |
+h |
|
−B |
|
Рис. 3.1. – Нелинейный элемент типа 4 – трехпозиционное реле с гистерезисом.
Для реализации этого нелинейного элемента в MatLab составим схему (Рис. 3.2).
Рис. 3.2. – Модель нелинейной системы.
Опытным путем найдем минимальное значение λmin относительной величины ширины петли гистерезиса λ = (h – c)/h = 1 – c/h, при которой возникают автоколебания. Параметры h и с фиксированы (h = 10, с = 4), зададим начальные условия системы (x0 = 4,
ν0 = 1). Опытным путем получено, что при значении параметра с = 2,9 возникают автоколебания, что соответствует λmin = 0,7, при увеличении параметра с система становится
10
