
Analitgeom_i_linal_ekzamen
.pdf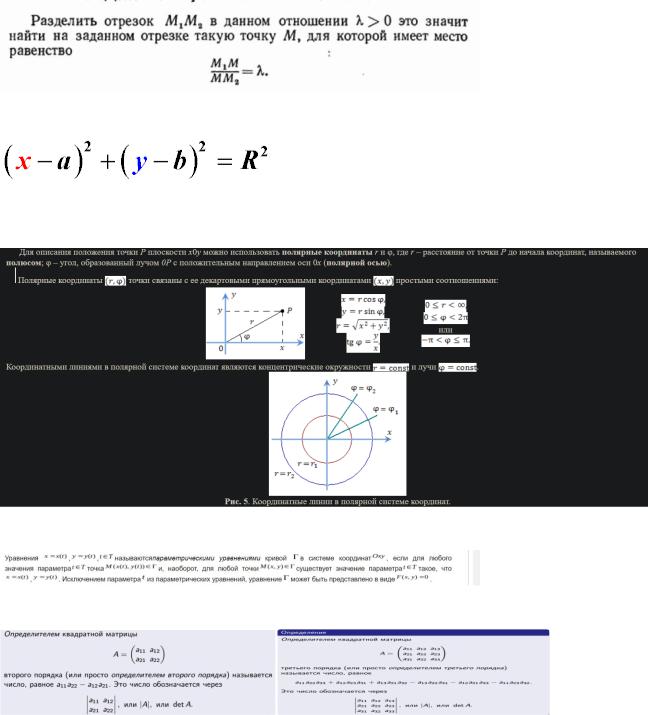
1.Деление отрезка в заданном отношении, деление отрезка пополам
2.Уравнение окружности с центром в точке (a, b) и радиусом R
3.Полярная система координат, полярные координаты точки, уравнение линии в полярных координатах.
4.Параметрические уравнения кривой на плоскости
5.Определители второго и третьего порядка
6.Свойства определителей
1.Величина определителя не изменяется при транспонировании. Свойства, справедливые для строк, будут справедливы для столбцов.
2.При перестановке двух строк величина определитель лишь изменит знак на противоположный.
3.Если все элементы строки определителя равны нулю, то определитель равен нулю.

4.Определитель, содержащий две одинаковые строки, равен нулю.
5.Общий множитель всех элементов какой-либо строки можно выносить за знак определителя.
6.Определитель, содержащий две пропорциональные строки, равен нулю.
7.Определитель порядка n равен сумме произведений элементов любой строки (столбца) и соответствующих им алгебраических дополнений:
7.Минор и алгебраическое дополнение данного элемента
8.1) Вектор, 2) длина вектора, 3) одинаковое и 4) противоположное направление двух векторов, 5) равенство двух векторов.
1)Вектор - это направленный отрезок, то есть отрезок, имеющий длину и определенное направление. 
2)Длина |AB|. направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB.
3)Два коллинеарных вектора a и b называются сонаправленными векторами,
если их направления совпадают: a↑↑b 
4)Два коллинеарных вектора a и b называются противоположно направленными векторами, если их направления противоположны: a↑↓b
5)Два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
a = b, если a↑↑b и |a| = |b|. 
9. Линейные операции над векторами и их свойства
Сложение векторов 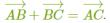 ;
; 
Вычитание векторов

Умножение векторов 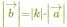
K>0 сонаправлены
K<0 - противополложно направлены
10. Коллинеарные векторы Вектора, параллельные одной прямой или лежащие на одной прямой называют
коллинеарными векторами
11. Компланарные векторы Вектора, параллельные одной плоскости или лежащие на одной плоскости называют
компланарными векторами.
12. Проекция вектора на ось, проекция вектора на вектор, вычисление проекций
Проекция вектора на ось – это вектор, началом и концом которого являются соответственно проекции начала и конца заданного вектора.
Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:

13. Координаты вектора. Линейные операции над векторами в координатной форме
14.Условие коллинеарности двух векторов
15.Скалярное произведение векторов и его свойства, скалярное произведение в координатной форме
16.Ортогональные векторы, условие ортогональности двух векторов
17.Правая тройка векторов
18.Векторное произведение и его свойства, векторное произведение в координатной форме
19.Векторное произведение для вычисления площади параллелограмма
20.Смешанное произведение векторов.
21. Смешанное произведение векторов для вычисления объема параллелепипеда

22. Направляющий и нормальный векторы данной прямой
Направляющий вектор прямой - это любой ненулевой вектор, лежащий на данной прямой или на параллельной ей прямой.
Нормальный вектор прямой - это любой ненулевой вектор, лежащий на любой прямой перпендикулярной данной.
23. Виды уравнений прямой на плоскости
общее уравнение прямой на плоскости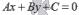
уравнением прямой в отрезках 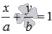 уравнением прямой с угловым коэффициентом
уравнением прямой с угловым коэффициентом 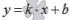
каноническое уравнение прямой на плоскости
параметрические уравнения прямой на плоскости 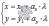 нормальное уравнение прямой
нормальное уравнение прямой 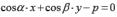
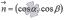
24.Формула расстояния от точки до прямой, формулы вычисления угла между прямыми
25.Условия параллельности и перпендикулярности двух прямых
26.Виды уравнений плоскости
Общее уравнение плоскости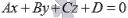
Уравнение плоскости в отрезках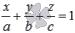
Нормальное уравнение плоскости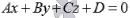

27. Формула расстояния от точки до плоскости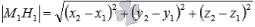 формулы вычисления угла между плоскостями
формулы вычисления угла между плоскостями

28. Виды уравнений прямой в пространстве |
|
Параметрические |
Канонические |
29.Кривые второго порядка: эллипс, гипербола, парабола (определения и их канонические уравнения)
Эллипс - множество точек на плоскости, сумма расстояний от каждой из которых до двух данных точек F1 и F2 есть величина постоянная, большая расстояния между этими точками.
F1 и F2 - фокусы.
Гипербола - множество точек на плоскости для каждой из которых абсолютная величина разности расстояний до двух данных точек F1 и F2 есть величина постоянная, меньшая расстояния между этими точками.
F1 и F2 - фокусы.
Парабола - множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.
F- фокус параболы, f - директриса параболы.
30.Поверхности второго порядка (канонические уравнения)
31. Матрица, ее элементы, обозначение, равенство матриц.
Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или
размерами матрицы.
Матрица обычно обозначаются заглавными буквами латинского алфавитв. Матрица содержащая n строк и m столбцов, называется матрицей размера n×m. При необходимости размер матрицы записывается следующим образом: An×m.

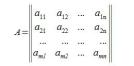 В матрице (1) числа
В матрице (1) числа 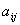 называются её элементами
называются её элементами
32. Матрица-строка - матрица, состоящая из одной строки 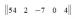
Матрица-столбец - матрица, состоящая из одного столбца 
Нулевая - матрица, все элементы которой равны нулю
Квадратная - матрица, у которой совпадает количество строк и столбцов
Треугольная - матрица, все элементы которой расположены под или над главной
диагональю (верх.треуг. матрица)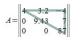 (ниж.треуг.матрица)
(ниж.треуг.матрица)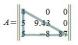
Диагональная - матрица, у которой равны нулю все элементы матрицы,
расположенные вне главной диагонали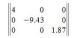
Единичная - матрица, у которой на главной диагонали стоят только единицы, а вне главной диагонали только нули 
33. Операции над матрицами

34. Определитель квадратной матрицы
треугольной матрицы
Определитель треугольной матрицы равен произведению элементов её главной диагонали,
единичной матрицы
единичной матрицы
Определитель единичной матрицы EE равен единице:
=detE=1
произведения матриц
Определитель произведения матриц равен произведению определителей этих матриц: det(A·B) = det(A)·det(B).
35.Обратная матрица: определение, условие существования, формула для вычисления
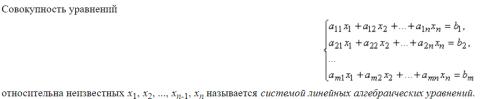
36.Система линейных уравнений, однородная и неоднородная система, решение системы, совместная и несовместная система,
Если среди правых частей bi системы есть хоть одна, отличная от нуля, то система называется
неоднородной системой линейных уравнений.
Если все правые части системы равны нулю, то система называется однородной.
Каждое решение совместной системы называется частным решением. Совокупность значений неизвестных, удовлетворяющая всем уравнениям системы, называется
решением системы.
Система, имеющая хотя бы одно решение, называется совместной. Система, у которой нет решений, называется несовместной.
37. Элементарные преобразования матриц.
1.умножение строки или столбца матрицы на ненулевое число;
2.перестановка местами двух строк или столбцов матрицы;
3.прибавление к некоторой строке матрицы другой ее строки, предварительно умноженной на произвольный коэффициент;
4.прибавление к некоторому столбцу матрицы другого ее столбца, предварительно умноженного на произвольный коэффициент.
Эквивалентные системы
Системы линейных уравнений называются эквивалентными, если множество их решений совпадает, то есть любое решение одной системы одновременно является решением другой, и наоборот.
Систему, эквивалентную данной, можно получить, в частности, заменив одно из уравнений на это уравнение, умноженное на любое отличное от нуля число. Эквивалентную систему можно получить также, заменив одно из уравнений суммой этого уравнения с другим уравнением системы. В общем, замена уравнения системы на линейную комбинацию уравнений даёт систему, эквивалентную исходной.
Система линейных алгебраических уравнений 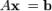 эквивалентна системе
эквивалентна системе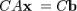 , где
, где  — невырожденная матрица.
— невырожденная матрица.
В частности, если сама матрица 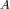 — невырожденная, и для неё существует обратная матрица
— невырожденная, и для неё существует обратная матрица 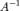 , то решение системы уравнений можно формально записать в виде
, то решение системы уравнений можно формально записать в виде
38. Матрица системы линейных уравнений, матричная форма записи системы
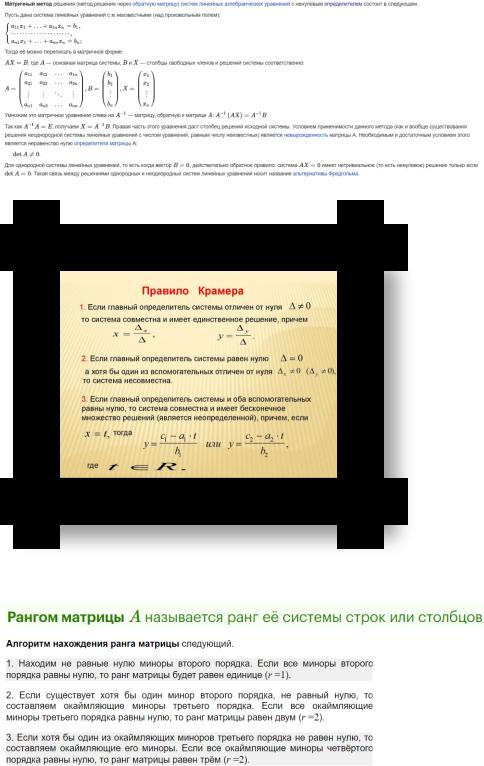
39. Правило Крамера
40. Ранг матрицы
41. Теорема Кронекера-Капелли
