3.1 Синтез контура регулирования момента

На рисунке 3.2 изображена структурная схема контура регулирования момента, в которую введено корректирующее устройство .

Рисунок 3.2 - Структурная схема контура регулирования момента с корректирующим устройством

Определим передаточную функцию корректирующего устройства в контуре регулирования момента (регулятора момента), решив уравнение

или

Тогда:

Таким образом, регулятор момента представляет собой ПД-регулятор, т.е.

где – коэффициент передачи ПД-регулятора;

- его постоянная времени

В этом случае передаточная функция разомкнутой цепи контура:

т.е. совпадает с передаточной функцией

Передаточная функция замкнутого контура регулирования момента по задающему воздействию:

Ниже приведен фрагмент файла, в котором рассчитаны ЛАЧХ, ЛФЧХ. переходная характеристика по задающему воздействию и определены показатели качества для скорректированного (синтезированного) контура регулирования момента. Расчет ЛАЧХ и ЛФЧХ производится по передаточной функции разомкнутой цепи, а переходная характеристика – по передаточной функции замкнутого контура регулирования момента по задающему воздействию. Само задающее воздействие рассчитано с учетом того, что установившееся значение момента будет равно пусковому моменту.

Расчётная формула для ЛАЧХ контура:

а

б

Рисунок 3.3 – ЛАЧХ (а) и ЛФЧХ (б) синтезированного контура регулирования момента

Частота среза:

Ожидаемое время переходного процесса в контуре (с):

Запас устойчивости по фазе (в градусах):

Запас устойчивости по амплитуде равен бесконечности, т.к. ЛФЧХ асимптотически стремится к значению -180 градусов

Расчет и построение переходной характеристики синтезированного контура. Определение основных показателей качества регулирования

Вектор коэффициентов характеристического полинома, сам характеристический полином, производная от него, корни характеристического уравнения и числитель передаточной функции замкнутого синтезированного контура регулирования момента.

Задающее воздействие (В):

Переходная функция контура регулирования момента:

Рисунок 3.4 – Переходная характеристика синтезированного контура регулирования момента

Время, соответствующее максимуму переходной характеристики (с), максимальное значение момента (А·В·с) и перерегулирование:

Время переходного процесса в контуре регулирования момента (с):

Вывод:

Расчёты показали, что контур точно настроен на технический оптимум. Перерегулирование не превышает 5%, время переходного процесса 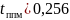немного больше ожидаемого .

Отношение заданного времени переходного процесса к времени переходного процесса внутреннего контура:

Для внутреннего контура по отношению к внешнему время переходного процесса должно быть не менее чем в два раза меньше времени переходного процесса для внешнего контура. Требования, поставленные в ТЗ, выполнены.

3.2 Синтез контура регулирования скорости

На рисунке 3.5 приведена структурная схема контура регулирования скорости. Здесь – передаточная функция замкнутого контура регулирования момента, в которой сделано допущение – опущен член при т.е.

Произведём настройку контура на ТО, учитывая, что для внешнего контура . Тогда передаточная функция:

(*)

или

Рисунок 3.5 – Синтезируемый контур регулирования скорости

Отсюда передаточная функция регулятора скорости:

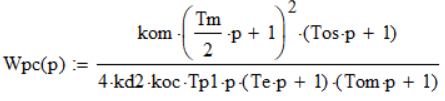
Таким образом, регулятор скорости представляет собой последовательное соединение ПИД-регулятора с передаточной функцией:

где:

и двухзвенного фильтра с передаточной функцией:

Т.к. постоянные времени фильтра и отличаются друг от друга больше чем в 5 раз ( ), то членом при пренебрегаем и заменяем двухзвенный фильтр однозвенным с передаточной функцией:

Получим передаточную функцию разомкнутой цепи для скорректированного контура регулирования скорости, подставив в формулу (*) передаточные функции регулятора, замкнутого внутреннего контура (без приближения, касающегося члена ), эквивалентного звена и звена обратной связи по скорости. Тогда:

1

Таким образом, из-за принятых допущений и приближений, порядок контура регулирования скорости – четвёртый, а не второй, как это имеет место для системы, настроенной на ТО.

Получим передаточную функцию замкнутого синтезированного контура регулирования скорости:

Ниже приведён фрагмент расчётного файла с характеристиками скорректированного контура регулирования скорости. ЛАЧХ и ЛФЧХ (рисунок 3.6) рассчитываются по передаточной функции разомкнутой цепи, а переходная характеристика (рисунок 3.7) – по передаточной функции .

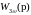Передаточная функция разомкнутой цепи для контура регулирования скорости при настройке на ТО:

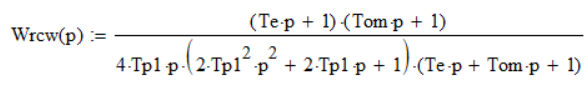
Формулы для расчёта ЛАЧХ и ЛФЧХ синтезированного контура регулирования скорости:

а

б

Рисунок 3.6 – ЛАЧХ (а) и ЛФЧХ (б) синтезированного контура

Частота среза (рад/с):

Частота переворота фазы (рад/с):

Запасы устойчивости по амплитуде (дБ) и фазе (в градусах):

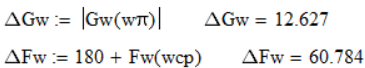
Запас устойчивости по амплитуде не бесконечный, а по фазе немного меньше, чем при точной настройке на ТО (66 градусов). Следует ожидать ухудшение качества регулирования.