
модел2
.pdf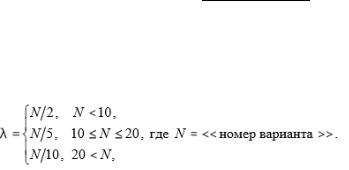
Практическая работа №2
«Моделирование случайных величин с заданным законом распределения»
Цель работы:
1)ознакомление с возможностями средств Excel и MATLAB по изучению основных законов распределений (ЗР) одномерных случайных величин (СВ);
2)исследование зависимости графиков функций распределения и функций плотности вероятности от параметров распределений;
3) изучение возможностей пакетов Excel и MATLAB по моделированию и анализу одномерных случайных величин.
Содержание и порядок выполнения работы
1. Необходимо выполнить следующие задания:
для каждого из следующих трех видов распределений (параметры распределений взять из п.2 данной работы):
нормального N(m, σ) (σ > 0),
равномерного R(a, b) (a < b),
экспоненциальногоE(λ) (λ > 0)
написать программу вывода в графическом окне графиков функций распределения с использованием функций Excel и MATLAB (см. приложение 1).
2. Написать программу, осуществляющую моделирование массивов объемом 300 для законов распределения: нормального, равномерного, экспоненциального (см. приложение 2).
Параметры моделируемых массивов:
– для нормального распределения N(m, σ) (σ> 0): m=<< номер варианта >>σ=<<√номер варианта>>;
–для равномерного распределения R(a ;b) (a<b): a=<<номер варианта>>, b= 2a;
–для экспоненциального распределения E(λ)( λ> 0 ):
Для каждого из этих массивов вывести в графическом окне график гистограммы относительных частот группированной выборки (шесть – восемь интервалов группировки).
Продемонстрировать полученные результаты преподавателю.
Замечание. Необходимо запомнить, как выглядят гистограммы выборок, полученных из генеральных совокупностей, имеющих нормальное, равномерное и экспоненциальное распределения.
Содержание отчета
Отчет, представленный на отдельных листах формата А4, должен содержать:
1.Титульный лист
2.Постановка задачи
3.Исходные данные по варианту
4.Аналитические выражения, применяемые в работе
5.Основные определения
6.Листинги программ (с комментариями) по расчету функций распределения, плотности вероятности и по моделированию СВ для нормального, равномерного, экспоненциального и релеевского ЗР;
7.Построенные графики функций распределения и плотности вероятности, а также графики гистограмм, моделируемых СВ.
8.Вычисленные оценки мат. ожидания, дисперсии, коэффициента асимметрии и эксцесса для выборки СВ длинной N=100, 1000, 1000, 10000 с помощью аналитических формул и с помощью функций Excel и MATLAB.
9.Построенные графики зависимости оценки мат. ожидания, дисперсии, коэффициента асимметрии и эксцесса от длины выборки.
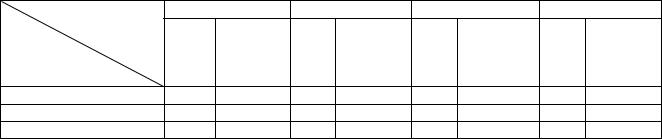
10.Таблицу cравнения теоретических числовых характеристик СВ и характеристик, полученных по моделируемой выборке
|
|
M[X] |
|
D[X] |
|
Ex[X] |
|
Sk[X] |
Характеристика |
теор. |
выбор. |
теор. |
выбор. |
теор. |
выбор. |
теор. |
выбор. |
Распределение |
|
N=102, |
|
N=102, |
|
N=102, |
|
N=102, |
|
|
103, 104, |
|
103, 104, |
|
103, 104, |
|
103, 104, |
|
|
105 |
|
105 |
|
105 |
|
105 |
Нормальное N(m, σ) |
|
|
|
|
|
|
|
|
Равномерное R(a, b) |
|
|
|
|
|
|
|
|
Экспоненциальное E(λ) |
|
|
|
|
|
|
|
|
11. Сделать выводы о проделанной работе. |
|
|
|
|
||||
Контрольные вопросы
Дайте определения:
закона распределения случайной величины;
функции распределения;
функции плотности вероятности;
случайной величины непрерывного типа, имеющей распределение: равномерное,
нормальное, гамма, экспоненциальное, Стьюдента, Фишера (необходимо уметь объяснять, от
скольких параметров зависит и каков их смысл).
Приложение 1. Средства MATLAB для изучения одномерных распределений
В пакете stats статистических программ MATLAB (каталог\MATLAB\toolbox\stats) имеются программы расчета плотностей вероятности и функций распределения для многих известных распределений. Имена функций для расчета плотностей вероятности оканчиваются буквами pdf
(probability density function)¸ а для расчета функций распределения – буквами cdf (cumulative distribution function).
Приложение 1.1. Функции MATLAB для расчета плотностей вероятности
y=unifpdf(x,a,b) – расчет значения плотности вероятности в точке x для равномерного на промежутке (a; b) распределения.
y=normpdf(x,m,sigma) – расчет значения плотности вероятности в точке x для нормального распределения, где m – математическое ожидание, sigma – среднее квадратическое отклонение
(СКО).
y=exppdf(x,lambda) – расчет значения плотности вероятности в точке x для экспоненциального распределения с параметром lambda, равным математическому ожиданию (!)
случайной величины.
Приложение 1.2. Функции MATLAB для расчета функций распределения y=unifcdf(x,a,b) – расчет значения функции распределения в точке x для равномерного на
промежутке (a; b) распределения.
y=normcdf(x,m,sigma) – расчет значения функции распределения в точке x для нормального распределения, где m – математическое ожидание, sigma – среднее квадратическое отклонение.
y=expcdf(x,lambda) – расчет значения функции распределения в точке x для экспо-
ненциального распределения с параметром lambda, равным математическому ожиданию (!)
случайной величины.
Приложение 2. Алгоритмы моделирования случайных величин
Случайные числа с различными законами распределения обычно моделируются с помощью преобразований одного или нескольких независимых значений базовой случайной величины.
Базовая случайная величина α – это случайная величина с распределением R(0;1) (равномерным распределением в интервале (0;1)). Независимые случайные величины с распределением R(0;1)
обозначаются символами α1, α2, … . В любой системе программирования имеется стандартная программа моделирования базовой случайной величины (см. функцию rand).
Рассмотрим алгоритмы моделирования случайных величин, имеющих равномерное,
нормальное и экспоненциальное распределение.

Равномерное распределение R(a,b), (a<b)
Если плотность вероятности ϕ(х) есть величина постоянная на определенном промежутке [a, b], то закон распределения называется равномерным. На рисунке ниже изображены графики функции распределения вероятностей и плотность вероятности равномерного закона распределения.
Аналитическое представление равномерного ЗР имеет вид
Функция распределения непрерывной случайной величины, выражается через плотность вероятности имеет вид
Аналитическое выражение для моделирования нормальной СВ имеет вид: X = a + (b - a)*α.
где α - независимые равномерно распределенные случайные величины на интервале [0; 1).
Алгоритм моделирования равномерно распределенной СВ:
1)задать параметр а==<<номер варианта>>;
2)вычислить b= 2a;
3)сгенерировать α ;
4)вычислить X = a + (b - a)*α.
5)Построить гистограмму
Решение задач в Excel
В качестве примера рассмотрим средства Моделирования СВ, имеющиеся в Excel, при подключении надстройки «Пакет анализа». Здесь имеются генераторы случайных чисел со следующими законами распределения:
1.Функция СЛЧИС, генерирующая случайные последовательности, равномерно распределенные на отрезке [0,1]. Ее синтаксис СЛЧИС() и она не имеет аргументов. Выделяется диапазон ячеек, вводится = СЛЧИС() и используется комбинация Ctrl+Shift+Enter.
2.Равномерное. Формирует равномерно распределенные последовательности в произвольном интервале [a, b]. Ее синтаксис =(b-a)*СЛЧИС()+a.
3.Нормальное. Генерирует нормальные последовательности с заданными математическим ожиданием и дисперсией.
Для имитации других распределений, отсутствующих в Еxcel, можно использовать,
например, метод обратных функций и датчик равномерно распределенных последовательностей.
Так например, методом обратных функций используя алгоритмы моделирования приведенные в работе можно смоделировать следующим образом:
Используя функцию =LN(СЛЧИС())/A1, записав значение λ в ячейку А1.
Аналогичным образом моделируются СВ распределенные по ЗР Релея.
Построение гистограммы.
1.Выделить мышкой столбцы таблицы, в которых будут отображены на осях гистограммы.
2.Находясь во вкладке «Вставка» нажимаем по кнопке «Гистограмма», которая расположена на ленте в блоке инструментов «Диаграммы».
3.В открывшемся списке выбираем один из пяти типов простых диаграмм:
o |
гистограмма; |
o |
объемная; |
o |
цилиндрическая; |
o |
коническая; |
o |
пирамидальная. |
Нормальное распределение N(m, σ), (σ > 0)
Среди законов распределения СВ наиболее распространённым является нормальный закон распределения. Нормальное распределение задаётся функцией плотности вероятности:
|
(x) |
|
1 |
exp |
|
|
|
2 |
|||
|
|
|
|
||
где |
параметр m — математическое |
ожидание, |
|||
отклонение (σ ² — дисперсия) распределения. |
|
|
|||
|
(x m) |
2 |
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
а параметр σ — среднеквадратическое
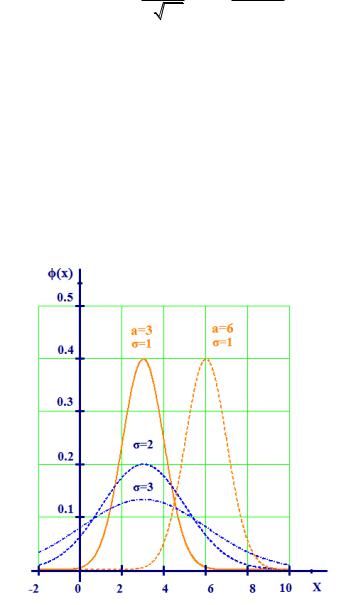
График плотности вероятности случайной величины, имеющей нормальный закон распределения, симметричен относительно прямой х=а, т.е. х равному математическому ожиданию.
При изменении величины математического ожидания кривая будет смещаться вдоль оси Ох. На графике (рисунок ниже) видно, что при х=3 кривая имеет максимум, т.к. математическое ожидание равно 3. Если математическое ожидание примет другое значение, например, а=6, то кривая будет иметь максимум при х=6. Говоря о среднем квадратическом отклонении, как можно увидеть из графика, чем больше среднее квадратическое отклонение, тем меньше максимальное значение плотности вероятности случайной величины
Рисунок – график функции плотности вероятности нормального ЗР
Аналитическое выражение для моделирования нормальной СВ имеет вид:
Y m |
2ln |
2 sin |
2 |
|
|
1 |
|
|
где α1 и α2 - независимые равномерно распределенные случайные числа на интервале [0; 1), m –
математическое ожидание СВ, σ – среднеквадратическое отклонение.
Алгоритм моделирования СВ состоит из следующих шагов:
1)сгенерировать α1 и α2
2)зарезервировать константу c = 2π;
3)= √−2lnα1;
4) φ =α2c ;
5)X1=r sin φ;
6)Y = m +σX1
Решение задач в пакете MATLAB
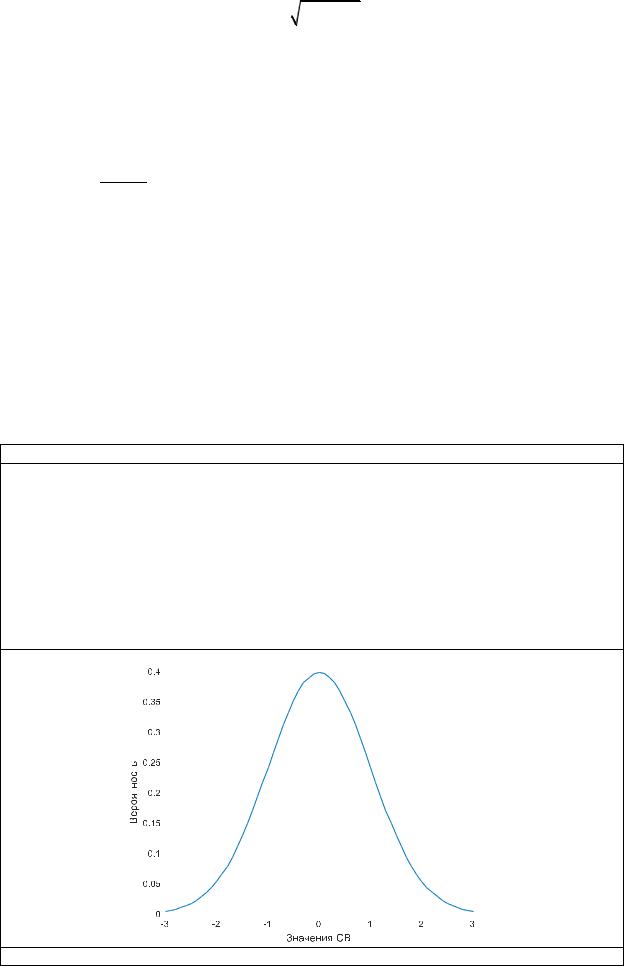
Построить функцию плотности распределения нормального закона
Функция плотности вероятности нормального закона f с математическим ожиданием Mx=0 и средним квадратическим отклонением sigma=1.
Листинг программы:
clear all |
|
close all |
|
Mx=0; |
% мат. ожижание |
sigma=1; |
% СКО |
x=Mx-3*sigma:0.1:Mx+3*sigma; |
% требуемый диапазон значений СВ |
f=normpdf(x, Mx, sigma); |
% расчет значений плотности вероятности |
figure() |
|
plot(x,f) |
% команда построение графика |
xlabel('Значения СВ') |
|
ylabel('Вероятность') |
|
Результат работы программы: |
|
Рисунок – график функции плотности вероятности нормального ЗР
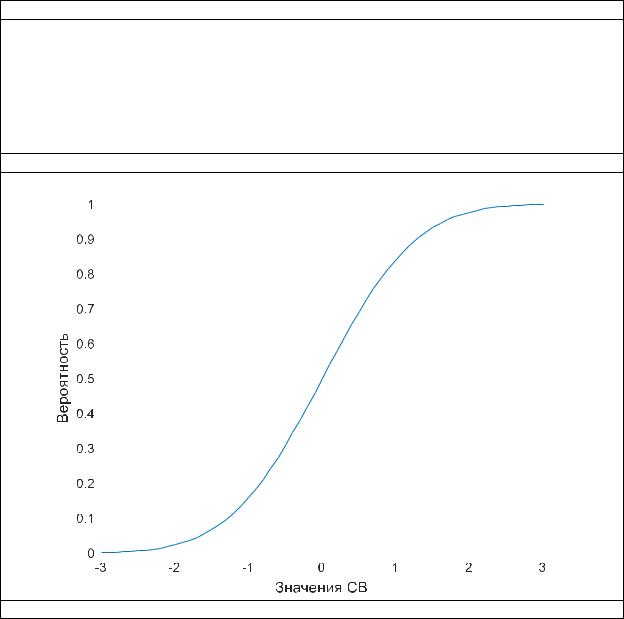
Построить функцию распределения вероятностей нормального ЗР
Функция распределения вероятностей нормального закона F с математическим ожиданием Mx=0 и средним квадратическим отклонением sigma=1.
Листинг программы:
Mx=0;
sigma=1;
x=Mx-3*sigma:0.1:Mx+3*sigma; % требуемый диапазон значений СВ
F=normcdf(x, Mx, sigma); % расчет значений функции распределения figure()
plot(x,F) xlabel('Значения СВ') ylabel('Вероятность')
Результат работы программы:
Рисунок – график функции нормального ЗР
Получить выборку заданной длины псевдо-СВ распределенных по нормальному закону с помощью функций MATLAB
Генерация выборки из N=1000 псевдослучайных чисел распределенных по нормальному закону с параметрами Mx=0 и sigma=1.
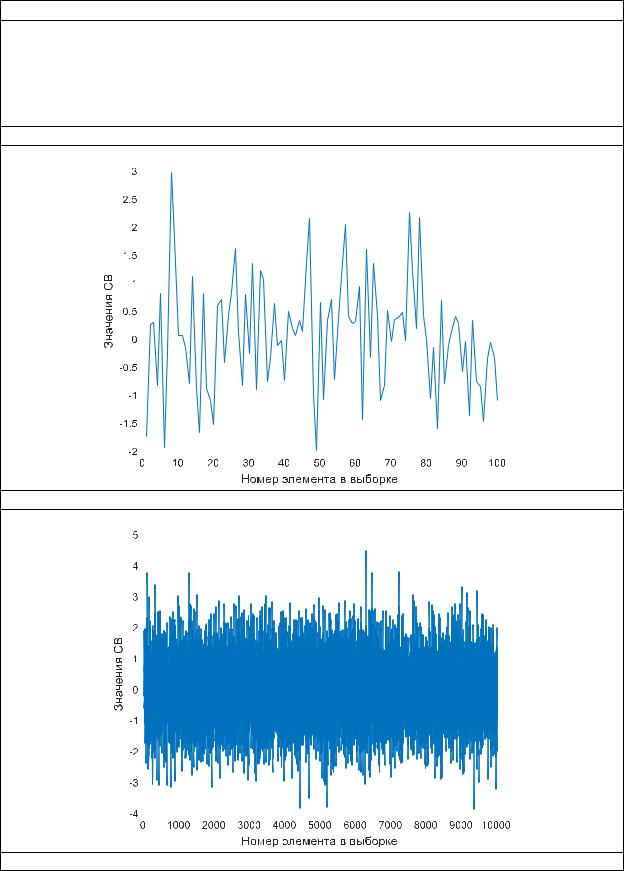
Листинг программы:
% моделирование с помощью функции MATLAB
Mx=0;
sigma=1;
N=10000;
Y=normrnd(Mx, sigma, N, 1); figure()
plot(Y)
Результат работы программы:
Рисунок – график функции нормального ЗР при N=100
Рисунок – график функции нормального ЗР при N= 10000
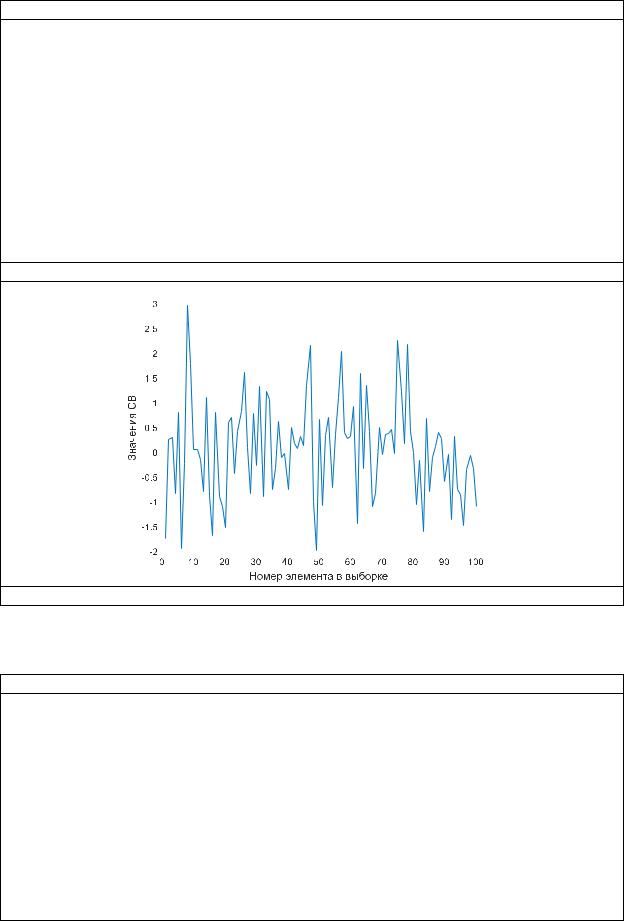
Моделирование СВ распределенных по нормальному закону с помощью алгоритма
Листинг программы:
clear all close all Mx=0; sigma=1; N=100; c=2*pi;
a1=rand(1,N); % сгенерировать a1 размерностью N a2=rand(1,N); % сгенерировать a2 размерностью N r=sqrt(-2*log(a1));
f=a2*c; X1=r.*sin(f); Y=Mx+sigma*X1; figure() plot(Y)
xlabel('Номер элемента в выборке') ylabel('Значения СВ')
Результат работы программы:
Рисунок – график функции нормального ЗР
Анализ и сравнение результатов
Листинг программы:
% проверка результатов
[kol_Y Y2]=hist(Y,50); p=kol_Y/N;
figure()
plot(Y2,p)
title('Нормальное распределение') xlabel('Значения СВ') ylabel('Вероятность')
figure()
histfit(Y,50) % графическое представление выборки Х с помощью гистограммы title('Гистограмма нормального распределения')
m_Y = mean (Y) % вычисление мат. ожидания st_Y = std(Y) % вычисление СКО
sk_Y = skewness(Y) % вычисление коэффициента асимметрии kur_Y = kurtosis(Y) % вычисление коэффициента эксцесса
