ЛР№2 Тайфун
.docxЦель работы: получение практических навыков исследования временных и спектральных характеристик сигналов в процессах их дискретизации и восстановления.
Задание:
Построить осциллограммы и спектрограммы исходного видеоимпульса формой, огибающей «треугольная», длительностью импульса.
Дискретизировать видеоимпульс и построить его осциллограммы и спектрограммы
Синтезировать восстанавливающие фильтры и построить осциллограммы и спектрограммы дискредитированного видеоимпульса после восстановления сигнала.
Исследовать как влияет частота среза ФНЧ на точность восстановления формы сигнала, на различие форм сигнала восстановленных разными ФНЧ
Оформить отчет
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
В настоящее время во всём мире развивается цифровая форма передачи сигналов: цифровая телефония, цифровое кабельное телевидение, цифровые системы коммутации и системы передачи, цифровые сети связи. Качество цифровой связи значительно выше, чем аналоговой, так как цифровые сигналы гораздо более помехоустойчивы: нет накопления шумов, легко обрабатываются, цифровые сигналы можно "сжимать", что позволяет в одной полосе частот организовать больше каналов с высокой скоростью передачи и отличным качеством.
Цифровой сигнал – это последовательность импульсов. Общепринято импульсную последовательность представлять, как чередование двух символов: 0 и 1. "Binary Digit" – "двоичная цифра". Отсюда и пошло понятие бит, то есть одна позиция в цифровом сигнале есть 1 бит; это может быть либо 0, либо 1. Восемь позиций в цифровом сигнале определяется понятием байт.
При передаче цифровых сигналов вводится понятие скорости передачи – это количество бит, передаваемых в единицу времени (в секунду).
Для передачи непрерывных сообщений цифровыми методами необходимо произвести преобразование этих сообщений в дискретные, которое осуществляется путём дискретизации непрерывных сигналов во времени и квантования их по уровню, и преобразования квантованных отсчётов в цифровой сигнал
Дискретизация - преобразование непрерывной функции в дискретную. Используется в гибридных вычислительных системах и цифровых устройствах при импульсно-кодовой модуляции сигналов в системах передачи данных. При передаче изображения используют для преобразования непрерывного аналогового сигнала в дискретный или дискретно-непрерывный сигнал. Обратный процесс называется восстановлением. При дискретизации только по времени, непрерывный аналоговый сигнал заменяется последовательностью отсчётов, величина которых может быть равна значению сигнала в данный момент времени. Возможность точного воспроизведения такого представления зависит от интервала времени между отсчётами Δt. Согласно теореме Котельникова: нет необходимости передавать бесконечное множество всех значений непрерывного сигнала x(t), достаточно передавать лишь те его значения, которые отстоят друг от друга на расстоянии ∆t = l/(2Fmax). Для восстановления сигнала x(t) на вход идеального фильтра низких частот, имеющего полосу пропускания частот от 0 до Fmsx, необходимо подать последовательность узких импульсов с амплитудой, соответствующей дискретным отсчетам сигнала x(ti) в моменты времени ti = i ∆t.
![]() ,
,
где Fmax - наибольшая частота спектра сигнала.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Задание 1
Исследование изменения формы и спектра сигнала при его дискретизации и восстановлении по отсчетам. Исследование влияния параметров фильтра-восстановителя сигнала на погрешность восстановления его формы.
Исходный видеоимпульс имеет треугольную форму огибающей, длительность импульса составляет 4 мс. Осциллограмма исходного видеоимпульса представлена на рисунке 1.
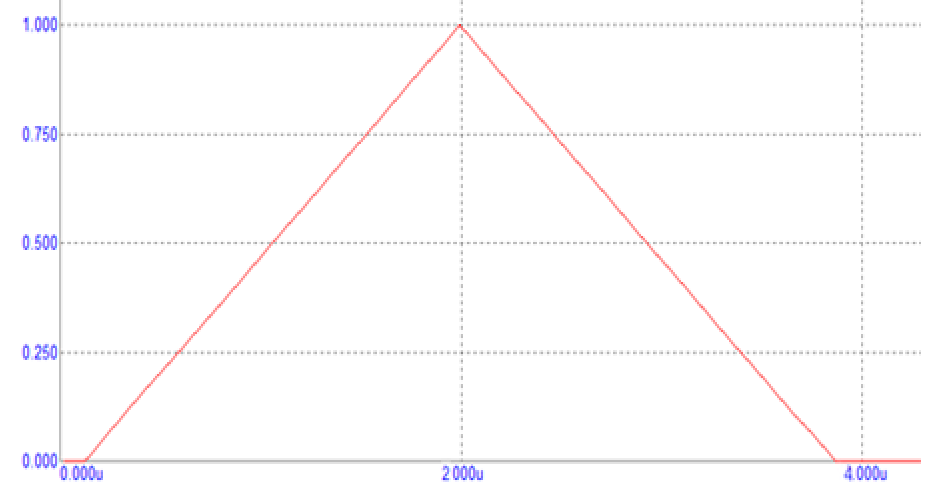
Рисунок 1 – Осцилограмма исходного видеоимпульса
Определим частоту дискретизации согласной теоремы Котельникова Fд = 2*Fсп и дискретизируем сигнал. Осцилограмма дискретизированного сигнала представлена на рисунке 2.
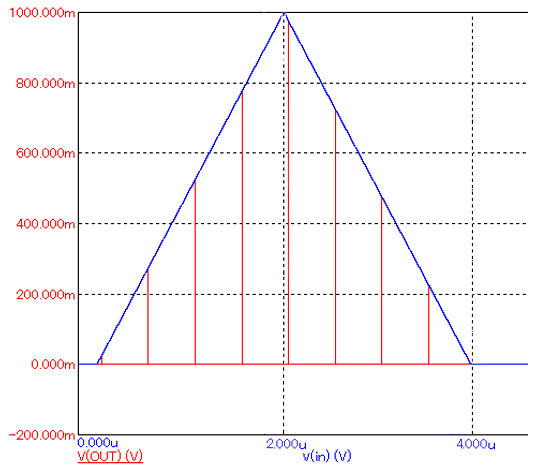
Рисунок 2 – Осцилограмма дискретизированного сигнала
Синтезируем ФНЧ1 с параметрами: частота среза ФНЧ1 = 1,1Fсп, частота задержания ФНЧ1 = 2,2 Fсп, величина потерь в полосе заграждения = 0дБ АЧХ синтезрованного фильтра представлена на рисунке 3.
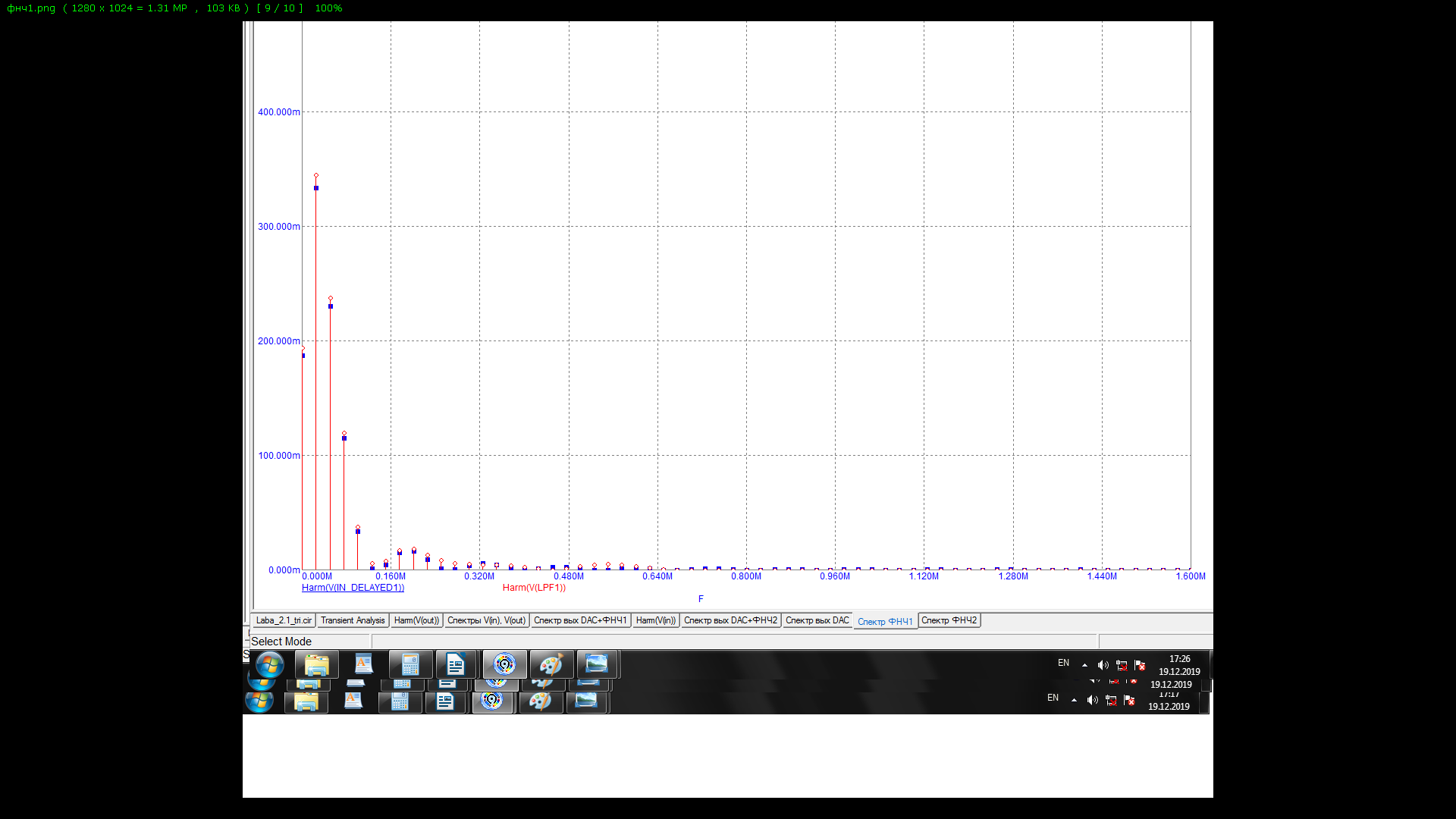 Рисунок
3 – АЧХ ФНЧ1
Рисунок
3 – АЧХ ФНЧ1
Задание 2
Исследование влияния частоты дискретизации сигнала на точность восстановления его формы. Исследование влияния параметров фильтра-восстановителя сигнала на погрешность восстановления его формы.
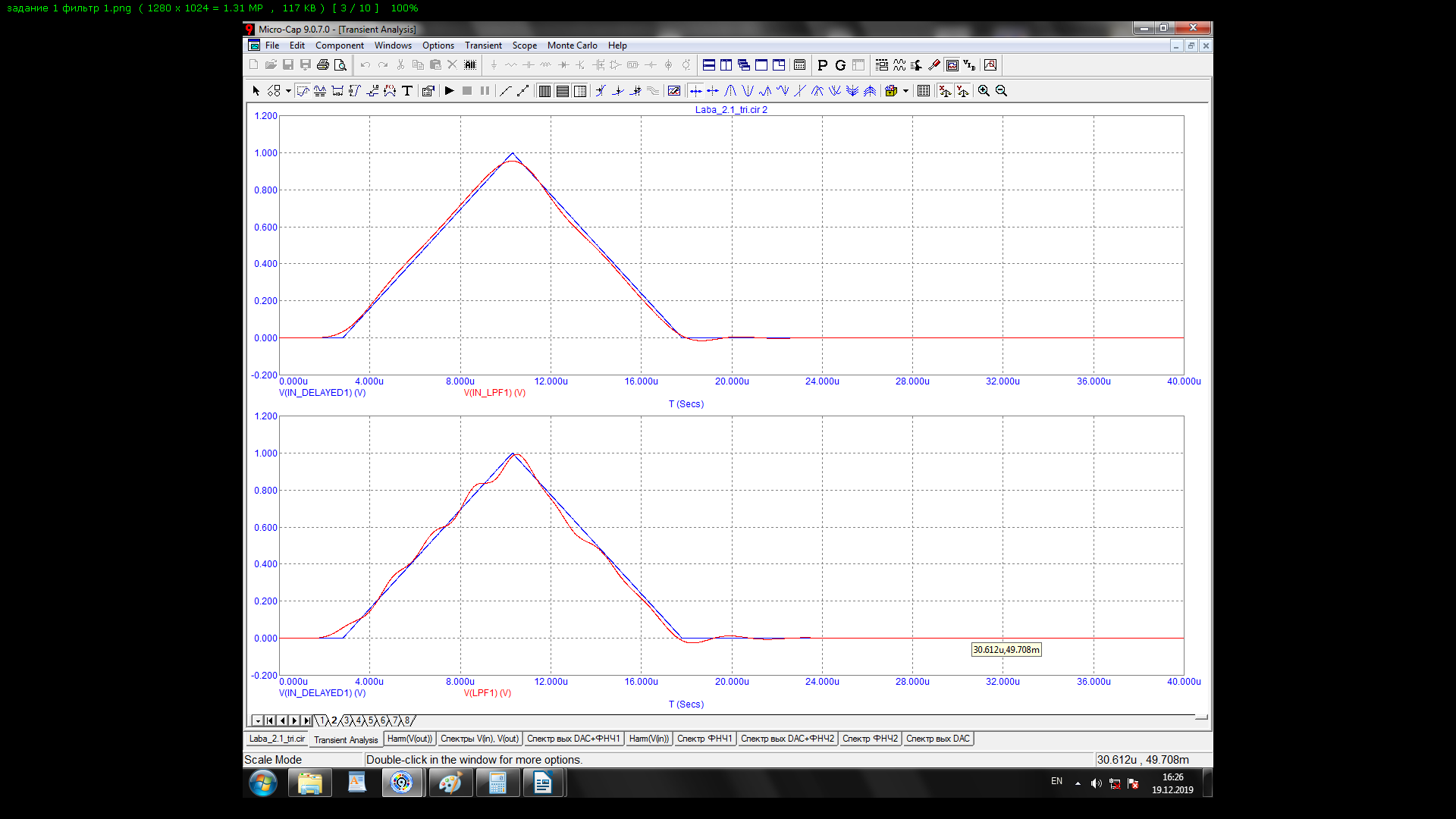
Осциллограмма и спектрограмма востановленного с помощью ФНЧ1 видеоимпульса представлены на рисунках 4 и 5 соотвественно.
|
|
Рисунок 4 – Осциллограмма восстановленного видеоимпульса

Рисунок 5 – Спектрограмма восстановленного видеоимпульса
Синтезируем восстанавливающий ФНЧ2 с отличными от ФНЧ1 параметрами: частота среза ФНЧ2 = 1,8Fсп, частота задержания ФНЧ1 = 3,6 Fсп, величина потерь в полосе заграждения = 0дБ АЧХ синтезрованного фильтра представлена на рисунке 6.

Рисунок 6 – АЧХ ФНЧ2
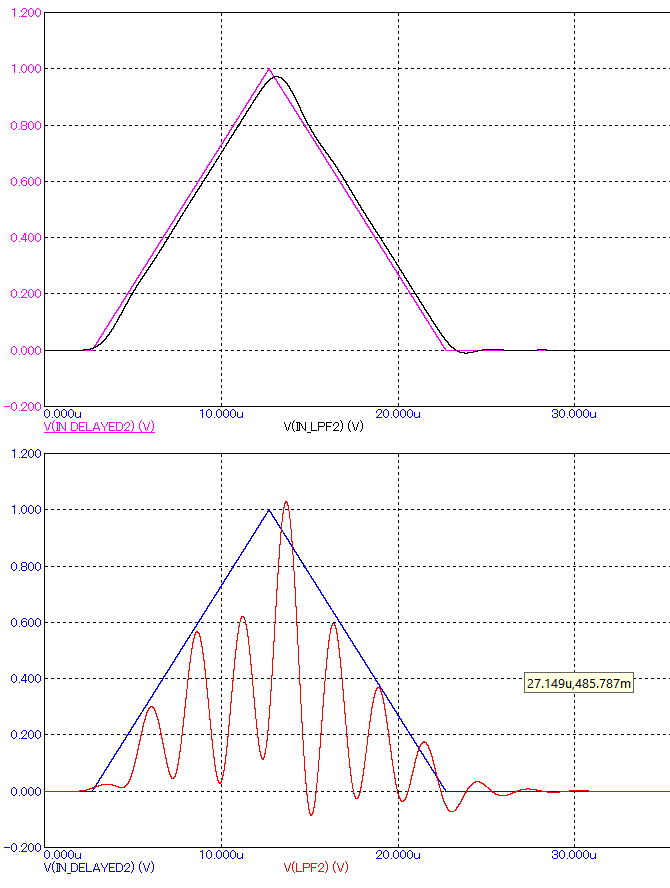
Осциллограмма и спектрограмма востановленного с помощью ФНЧ2 видеоимпульса представлены на рисунках 7.
|
|
Рисунок 7 – АЧХ ФНЧ2
Как видим во втором случае ФНЧ2 имеет слишком высокую ширину пропускания, вследствии чего часть второго лепестка не фильтруется и точность восстановления сигнала сильно падает. Различие в точности восстановления сигналов ФНЧ1 и ФНЧ2 предсатвлено на рисунке 8.
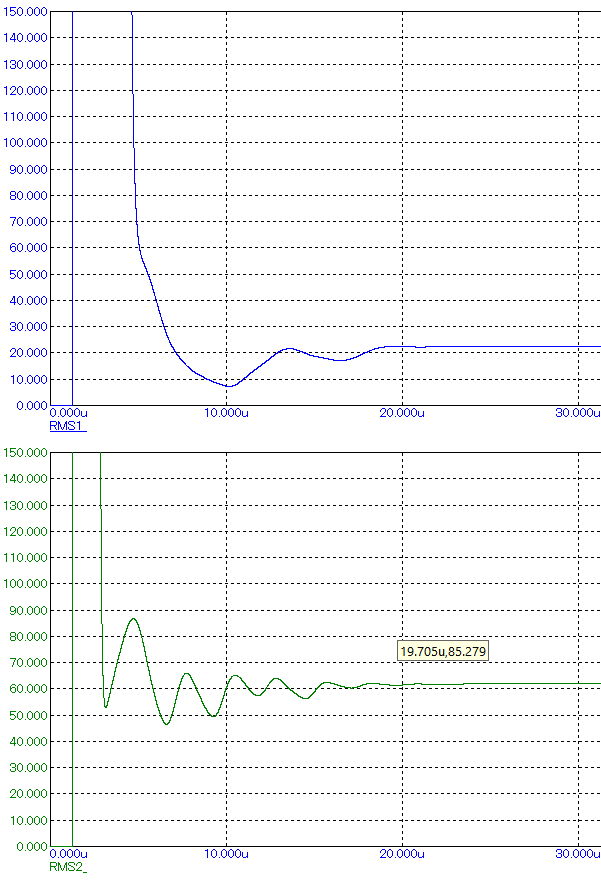
Рисунок 8 – Точность восстановления видеоимпульса
Вывод: в ходе выполнений лабораторной работы были получены практические навыки исследования временных и спектральных характеристик сигналов в процессах их дискретизации и восстановления.