ММО_лаб1_отчет_Черкашин
.docxМіністерство освіти і науки України
Харківський національний університет радіоелектроніки
Кафедра системотехніки
Дисципліна: «Математичні методи оптимізації»
ЛАБОРАТОРНА РОБОТА № 1
«РОЗВ’ЯЗАННЯ ТРАНСПОРТНОЇ ЗАДАЧІ»
Виконали: ст. гр. КСУАм-20 Черкашин В.А.
|
|
Прийняв: доцент кафедри СТ Калита Н. І. з оцінкою «____________» «____»_______________2020 р. |
Харків 2020
1 РОЗВ’ЯЗАННЯ ТРАНСПОРТНОЇ ЗАДАЧІ
1.1 Мета роботи
Вивчення особливостей задач дискретної оптимізації. Формалізація транспортної задачі та її розв’язування.
1.2 Організація самостійної роботи
До лабораторної роботи за конспектом лекцій та рекомендованою літературою [х– х] вивчити теоретичний матеріал щодо аналізу та розв’язання задач дискретної оптимізації. З’ясувати сутність етапів розв’язання транспортної задачі з використанням методів:
мінімального елемента;
Фогеля;
північно-західного кута;
потенціалів.
1.3 Склад лабораторного устаткування
Лабораторна робота виконується на обчислювальному комплексі, у складі якого: локальна обчислювальна мережа комп'ютерів типу IBM PC, OC Windows XP.
1.4 Хід роботи
1.4.1 Для обраної предметної області скласти задачу, яка підпадає у клас транспортних задач.
У звязку з пандемією короновірусу найбільші фармацевтичні компанії: StartMed (США), VacCOM (Велекобритнія), CityJerkOff (Китай), Svager (Німеччина) синтезують вакцину від коронавірусу у кількості 655, 370, 790, 455 тисяч ампул відповідно. Продукція однорідна, а величина mi – ресурсом. Є 5 країн, яким необхідно експортувати цю продукцію: Японія, Укаїна, Франція, Литва, Польша за допомогою літаків, тобто відомі необхідну кількість ампул: 250, 393, 536, 260, 282, тисяч ампул відповідно, величина rj – замовлення. Також відома вартість перевезень з компанії виробника в країну споживача.
Необхідно знайти план перевезень (xij) з i-того пункту в j-тий, щоб вся продукція не була перевищена і всі замовлення були виконані, а також загальна вартість експортування була мінімальною (Pij – вартість експортування ампул з і-того пункту в j-тий).
Таблиця 1.1 – Транспортна таблиця задачі
|
B1 |
B2 |
B3 |
B4 |
B5 |
mi |
A1 |
10 |
2 |
7 |
5 |
8 |
655 |
A2 |
20 |
4 |
10 |
7 |
8 |
370 |
A3 |
4 |
9 |
2 |
3 |
4 |
790 |
A4 |
18 |
20 |
13 |
7 |
1 |
455 |
rj |
250 |
393 |
536 |
260 |
282 |
|
1.4.2 Виконати формалізацію задачі і розробити її математичну модель. Проаналізувати модель з огляду на її збалансованість і, якщо необхідно, привести її до збалансованого виду.
Математична модель транспортної задачі:
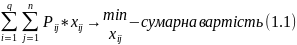
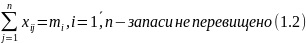
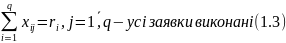
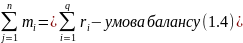
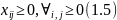
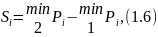
де
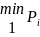– найменша вартість,
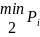– наступна за найменшою
вартістю;
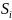– штраф (різниця) і-того рядку;
– штраф (різниця) j-того
стовпця;
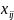– кількість вантажу, який
треба перевезти з і-того пункту в j-тий;
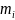– ресурси (запаси);
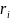– замовлення (потреби, заявки).
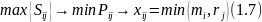
Так як умова (1.4) не виконується (ресурсів більше ніж заявок), був введений фіктивний споживач, щоб умова (1.4) виконувалась (таблиця 1.2).
Таблиця 1.2 – Транспортна таблиця з фіктивним споживачом.
|
B1 |
B2 |
B3 |
B4 |
B5 |
B6 |
mi |
A1 |
10 |
2 |
7 |
5 |
8 |
0 |
655 |
A2 |
20 |
4 |
10 |
7 |
8 |
0 |
370 |
A3 |
4 |
9 |
2 |
3 |
4 |
0 |
790 |
A4 |
18 |
20 |
13 |
7 |
1 |
0 |
455 |
rj |
250 |
393 |
536 |
260 |
282 |
449 |
|
1.4.3 Опис алгоритмів застосованих при вирішенні задачі.
1.4.3.1 Метод мінімального елементу
Побудова вихідного опорного
плану починають з
визначення комірки, яка має найменшу
вартість перевезень. Припустимо, що
такою являється комірка, що міститься
на перетині 
-го
рядка та 
-го
стовпця. Тоді, із співвідношення 
знаходимо
значення об'єму перевезень від
постачальника 
до
споживача 
.
Зазначимо, що при цьому, як і у випадку
з методом північно-західного кута,
можливі три варіанти:
Якщо
,
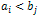то 
,
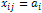-й рядок виключається
з подальшого розгляду (запаси
постачальника
повністю вичерпані), а
потреби 
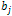споживача
зменшується
на величину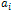 
.Якщо
,
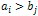то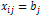 
,
-й стовпець виключається
з подальшого розгляду (потреби
споживача
повністю задоволені),
а наявність вантажу
постачальника
зменшується
на величину
.Якщо
,
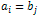то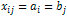 
,
-й рядок та
-й стовбець виключаються
з подальшого розгляду. Даний варіант
призводить до виродження вихідного
плану.
Далі, знову-таки, вибирають вільну комірку з найменшою вартістю, і заповнюють її. Обчислювальний процес методу мінімальної вартості продовжується до тих пір, поки всі запаси не будуть вичерпані і всі потреби — задоволені.
1.4.3.2 Метод потенціалів
Нехай
кожен пункт відправлення Ai
платить за вивіз одиниці вантажу платіж
αi.
І кожен пункт призначення Вj
платить за привезення одиниці вантажу
βj.
Ці платежі передаються посереднику.
Таким чином, на маршруті ij
він отримує
.
Назвемо цю величину псевдовартість.
Виявляється, що сумарна псевдовартість
плану перевезень є величина постійна
(не змінюється зі зміною плану). У цьому
полягає теорема про платежі.
Для доказу запишемо формулу псевдовартості і перегрупіруємо складові:
(2.8)
Теорема про потенційний плані ТЗ.
Нехай
в базисних клітинах вартість перевезень
дорівнює псевдовартості перевезень
,
а у вільних клітинах
,
тоді такий план є оптимальним і поліпшений
бути не може.
(*)
(2.9)
Знак (*) означає, що виконується умова (*). Тобто необхідно показати, що вартість плану X* є нижньою межею і визначається тільки вихідними даними завдання.
(тому що в базисної
,
а в порожній дорівнює нулю). Перейдемо
до іншого безпідставного плану:
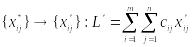
В
цьому плані перевезення з базисної
клітини потрапила в вільну, де
.
Тобто будь-яка зміна плану від
призводить до збільшення вартості, отже
план {x*ij}
є оптимальним.
Ідея методу потенціалів ґрунтується на цій теоремі і полягає в наступному.
1) Складемо будь опорний план і, якщо це необхідно, то доповнимо до невиродженого.
2) Зажадаємо в базисної клітці . Запишемо в лівому верхньому кутку базисної клітини величини псевдовартостей, рівні вартостей, які стоять в правому верхньому куті. Таких клітин m + n - 1.
3)
Знаходимо невідомі нам платежі
і
з умов, що їх сума відома для кожної
базисної клітини.
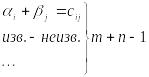
У
такій системі в кожному рядку дві
невідомих, а всього їх (m + n). Оскільки
рівності всього (m + n -1), то рішень безліч.
Тому будемо брати довільне
і думати, наприклад,
.
Тоді можна почати рішення з рядка, де
міститься
і так послідовно переходячи в рядки з
відомим платежем знайти всі платежі.
4)
Знайшовши всі платежі
,
підраховуємо для вільних клітин.
5)
Перевіряємо умову (*) для вільних клітин.
Там, де
,
вільна клітина дає цикл з негативною
ціною, тому що
.
6)
Вибираємо цикл з найменшим (найбільш
негативним)
і складаємо цикл. За циклу переносимо
k одиниць
вантажу і продовжуємо так далі до
виконання умови (*).
1.4.3 Згідно варіанта індивідуального завдання розробити алгоритм пошуку опорного плану і оптимального плану. Виконати програмну реалізацію, провести обчислювальні експерименти.
Згідно варіанту завдання була розроблена програмна реалізація знаходження опорного плану методом мінімального елементу транспортної задачі та оптимального плану методом потенціалів, код якої представлений у Додатку А. Також були отримані результати розрахунків, які зображені на рисунку 1.1
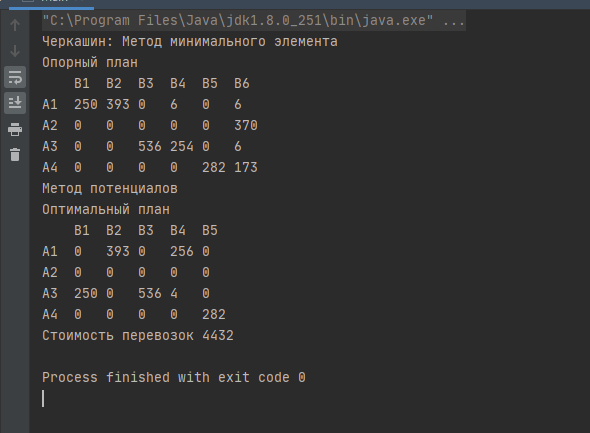
Рисунок 1.1 – Результат виконання програми
ВИСНОВКИ
У ході лабораторної роботи були вивчені особливості задач дискретної оптимізації, а також здійснена формалізація транспортної задачі та її розв’язання.
Згідно індивідуального завдання була складена умова задачі, яка підлягає під клас транспортних задач. Також задача була штучно зведена до збалансованої задачі шляхом введення фіктивного споживача. Був розроблений алгоритм та програмна реалізація знаходження опорного плану транспортної задачі методом мінімального елементу, а також пошук оптимального плану методом потенціалів.
Проаналізувавши результат виконання розробленої програми було визначено, що за методом мінімального елемента опорний план не є оптимальним і може бути вдосконалений наприклад за методом потенціалів.
Додаток А
Текст програми
public class Main {
static int x;
static int y;
static int buff;
public static int getX() {
return x;
}
public static void setX(int a) {
x = a;
}
public static int getY() {
return y;
}
public static void setY(int b) {
y = b;
}
public static int getBuff() {
return buff;
}
public static void setBuff(int buf) {
buff = buf;
}
public static int[] strafSi(int rows, int col, int res[][], int A[]) {
int[] Si = new int[rows];
for (int i = 0; i < rows; i++) {
int min = Integer.MAX_VALUE;
int min1 = Integer.MAX_VALUE;
for (int j = 0; j < col - 1; j++) {
for (int k = 1; k < col - 1; k++) {
if (res[i][k] != 1111) {
if (min > res[i][k]) {
min = res[i][k];
}
}
}
if (res[i][j] != 1111 || res[i][j] < 1111) {
if (res[i][j] != min) {
if (min1 > res[i][j]) {
min1 = res[i][j];
}
}
}
}
Si[i] = min1 - min;
}
for (int i = 0; i < rows; i++) {
if (A[i] == 0) {
Si[i] = 0;
}
}
return Si;
}
public static int[][] Fogel(int rows, int col, int res[][], int Si[], int Sj[], int A[], int B[]) {
int maxi = 0, maxj = 0;
int indI = 0, indJ = 0, index = 0, index1 = 0;
int min = Integer.MAX_VALUE;
for (int i = 0; i < Si.length; i++) {
if (maxi < Si[i]) {
maxi = Si[i];
indI = i;
}
}
for (int i = 0; i < Sj.length; i++) {
if (maxj < Sj[i]) {
maxj = Sj[i];
indJ = i;
}
}
if (maxi >= maxj) {
for (int j = 0; j < col - 1; j++) {
if (res[indI][j] < min) {
min = res[indI][j];
index = j;
index1 = indI;
}
}
} else {
for (int i = 0; i < rows; i++) {
if (res[i][indJ] < min) {
min = res[i][indJ];
index = indJ;
index1 = i;
}
}
}
if (A[index1] >= B[index]) {
A[index1] -= B[index];
res[index1][index] = B[index];
setBuff(res[index1][index]);
B[index] = 0;
for (int i = 0; i < rows; i++) {
res[i][index] = 1111;
}
} else {
B[index] -= A[index1];
res[index1][index] = A[index1];
setBuff(res[index1][index]);
A[index1] = 0;
for (int i = 0; i < col - 1; i++) {
res[index1][i] = 1111;
}
}
for (int i = 0; i < A.length; i++) {
if (A[i] == 0) {
Si[i] = 0;
}
}
for (int i = 0; i < B.length; i++) {
if (B[i] == 0) {
Sj[i] = 0;
}
}
setX(index1);
setY(index);
return res;
}
public static int[] strafSj(int rows, int col, int res[][], int B[]) {
int[] Sj = new int[col];
for (int i = 0; i < col; i++) {
int min = Integer.MAX_VALUE;
int min1 = Integer.MAX_VALUE;
sout(Черкашин метод минимального елементу)
for (int j = 0; j < rows; j++) {
for (int k = 1; k < rows; k++) {
if (min > res[k][i]) {
min = res[k][i];
}
}
if (res[j][i] != 1111 || res[j][i] < 1111) {
if (res[j][i] != min) {
if (min1 > res[j][i]) {
min1 = res[j][i];
}
}
}
// }}else {min1=0;}
}
Sj[i] = Math.abs(min1 - min);
}
Sout(Метод потенциалов)
Sj[col - 1] = 0;
for (int i = 0; i < col; i++) {
if (B[i] == 0) {
Sj[i] = 0;
}
}
return Sj;
}