ММО_ЛР-4_Черкашин

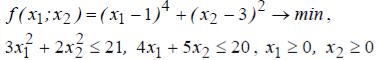
4 РОЗВ’ЯЗУВАННЯ ЗАДАЧ НЕЛІНІЙНОГО ПРОГРАМУВАННЯ МЕТОДАМИ БАР'ЄРНИХ ТА ШТРАФНИХ ФУНКЦІЙ

4.1 Мета роботи

Вивчення задач нелінійного програмування з обмеженнями-

нерівностями та методів їх розв'язування. Формалізація алгоритмів,

програмна реалізація та проведення обчислювальних експериментів,

дослідження поведінки методів при різних вхідних даних.

4.2 Склад лабораторного устаткування

Лабораторна робота виконується на обчислювальному комплексі з конфігурацією, достатньому для функціонування ОС, середовища розробки програмного забезпечення та проведення обчислювальних експериментів.

4.3 Хід роботи

4.3.1 Постановка завдання

Використовуючи метод штрафних функцій, знайти мінімум функцій при заданих обмеженнях

4.3.2 Опис методу штрафних функцій

Вихідна задача нелінійного програмування з обмеженнями замінюється послідовністю задач безумовної оптимізації (тобто без обмежень) за рахунок

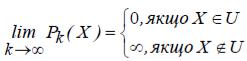
введення нової функції, яка враховує невиконання обмежень у вигляді

«штрафу»

(4.1)

де F(X) – цільова функція, P(X) – функція, що дорівнює в ідеалі F(X) в

області допустимих рішень U і дорівнює нескінченності поза цією областю.

Практично замість P(X) підбирається послідовність функцій Pk(X) , що залежать від k, так, щоб

Послідовність штрафних функцій {Pk ( X )} має властивість:

При певних умовах послідовність розв'язків X(k) задач безумовної оптимізації (4.8) збігається до розв'язку вхідної задачі X* , і для достатньо великих k вважають

В якості критерію досягнення заданої точності може бути нерівність

X (k ) X (k / 2)

де ε > 0 – задана точність, k – парне число.

4.4 Програмна реалізація алгоритму

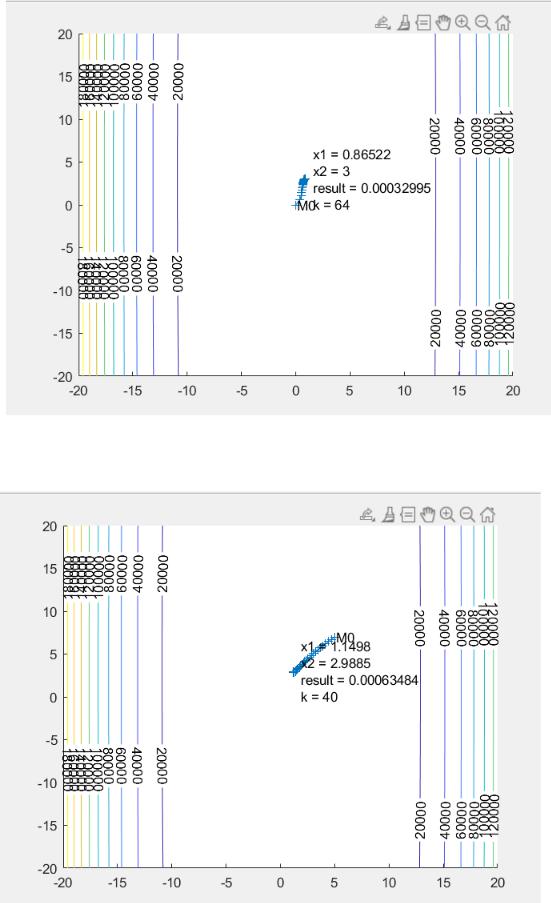
Рисунок 4.1 – Точність дорівнює 0.1, початкова точка (0:0)

Рисунок 4.2 – Точність дорівнює 0.1, початкова точка (5:7)

Рисунок 4.3 – Точність дорівнює 0.1, початкова точка (50:30)

Рисунок 4.4 – Приклад роботи алгоритма при іншій цільовій функції та обмеженнь

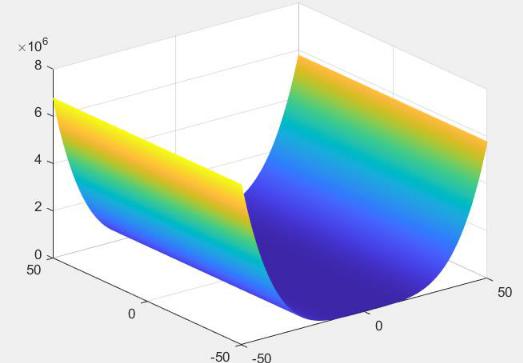
Рисунок 4.5 – 3D графік функції

ВИСНОВКИ

В ході виконання лабароторної роботи були розглянуті задачі нелінійного програмування з обмеженнями та метод їх розв'язування, а саме штрафні функції.

Процес знаходження рішення методом штрафних функцій описується наступним алгоритмом:

1.Визначають початкову точку, що належить допустимій множині.

2.Вибирають величину кроку γ градієнтного методу.

3.Перехід до нової точки.

4.Перевіряють, чи задовольняють координати нової точки системі обмежень. Якщо нова точка належить допустимій множині, перевіряють правило зупинки, і якщо воно не виконується, повертаються до пункту 3.

Якщо правило зупинки виконано, отримана точка і є рішення задачі.

5. Якщо точка, знайдена в пункті 3, не належить допустимому безлічі,

то вибирають коефіцієнт штрафу для того обмеження, яке порушено. При цьому коефіцієнт штрафу або призначають заздалегідь, або розраховують як в методі Ерроу-Гурвіца. Після цього повертаються до пункту 3.

Додаток А

Текст програми

if g(x1, x2) < 22; step_x1 = dfdx1(x1, x2); step_x2 = dfdx2(x1, x2); else

step_x1 = alpha*dgdx1(x1, x2); step_x2 = alpha*dgdx2(x1, x2); end

new_x1 = x1 + gamma*step_x1; new_x2 = x2 + gamma*step_x2; x1trace(i) = new_x1; x2trace(i) = new_x2;

i = i + 1; x1 = new_x1; x2 = new_x2;

k = k + 1; end

x = -50:0.1:50; y = -50:0.1:50;

[X, Y] = meshgrid(x, y); hold on;

Z = (X - 1).^4 + (Y-3).^2; [C, h] = contour(X, Y, Z); clabel(C, h);

plot(x1trace, x2trace, '-+'); text(x1trace(1) + 0.1, x2trace(1), 'M0');

result = (x1-1)*(x1-1)*(x1-1)*(x1-1) + (x2-3)*(x2-3) text(x1 + 0.7, x2, ...

strvcat(['x1 = ' num2str(x1)], ...

['x2 = ' num2str(x2)], ...

['result = ' num2str(result)], ...

['k = ' num2str(k)]));