
ИДЗ Рябушко РЕШЕНИЯ / ИДЗ 3.2-2
.pdf
ИДЗ 3.2 – Вариант 2
Даны вершины треугольника ABC: A(x1, y1), B(x2, y2), C(x3, y3). Найти: а) уравнение стороны AB
б) уравнение высоты CH
в) уравнение медианы AM
г) точку N пересечения медианы AM и высоты CH
д) уравнение прямой, проходящей через вершину С параллельно стороне AB е) расстояние от точки С до прямой AB
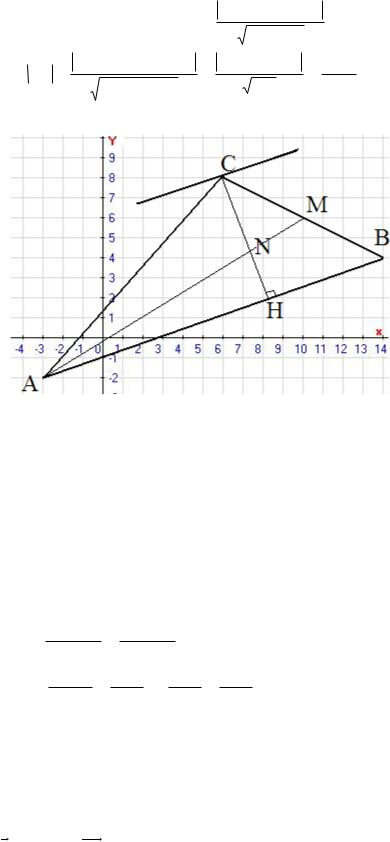
1.2 A(−3, −2) B(14, 4) C(6, 8)
а) уравнение стороны AB
Воспользовавшись уравнением прямой, проходящей через две точки, получим уравнение стороны АВ:
x x |
A |
|
y y |
A |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x |
|
x |
|
y |
|
y |
|
|
|
|
|
|
|
|
|
|
|
||||
B |
A |
|
B |
A |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x 3 |
|
y 2 |
|
x 3 |
|
y 2 |
|
|
|
|
|
|
|
|
|||||||
14 3 |
4 2 |
|
17 |
6 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
6(x 3) 17(y 2) |
|
|
|
|
|
|
|
|
|
|
|||||||||||
6x 18 17y 34 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
6x 18 17y 34 0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
6x − 17y − 16 = 0 − уравнение стороны AB |
|
|
|
|
|
||||||||||||||||
б) уравнение высоты CH |
|
|
|
|
|
|
|
|
|||||||||||||
Согласно уравнению y = kx + b, |
y |
6 |
x |
16 |
; угловой коэффициент прямой AB k1 |
|
6 |
. С |
|||||||||||||
17 |
17 |
17 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
учетом условия перпендикулярности прямых АВ и СН tg k 2 k1 , угловой коэффициент
1 k1k 2
высоты СН k 2 |
1 |
|
1 (k1k2 = −1). |
|
|
|||||
|
|
|
|
|
||||||
|
|
|
k1 |
|
6 |
|
|
|
||
|
|
|
|
17 |
|
|
|
|||
По точке C(6, 8) и угловому коэффициенту k 2 |
17 |
составляем уравнение высоты СН |
||||||||
6 |
||||||||||
|
|
|
|
|
|
|
|
|
||
Уравнение прямой проходящей через две точки |
|
|
||||||||
|
|
|
|
|
|
|
y − y0 = k(x − x0) |
|
||
Тогда уравнение высоты CH запишется в виде: |
|
|
||||||||
|
|
|
|
|
|
|
y − yC = k2(x − xC) |
|
||
y 8 |
17 |
(x |
6) |
|
|
|||||
6 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
||
6y 48 17x 102 |
|
|
||||||||
6y 48 17x 102 0 |
|
|
||||||||
17x + 6y − 150 = 0 − уравнение высоты CH |
|
|
||||||||
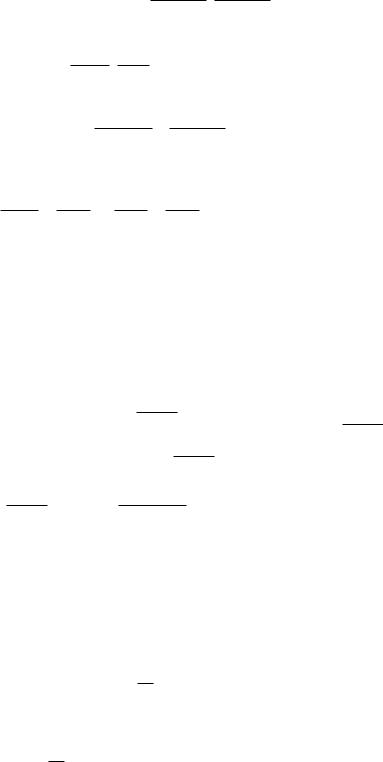
в) уравнение медианы AM
По известным формулам |
|
|||
M |
||||
|
|
|
|
|
BC |
|
|
|
|
14 6 |
; |
4 8 |
||
M |
|
|
|
|
|
2 |
|
|
2 |
x B
x |
C |
; |
y |
B |
y |
C |
|
|
|
||||
2 |
|
|
|
2 |
|
|
|
|
|
|
|
||
M 10 ; 6 |
|
|||||
находим координаты x,y середины М отрезка
Воспользуемся уравнением прямой, проходящей через две точки
x x |
A |
|
y y |
A |
||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||
x |
M |
x |
A |
|
y |
M |
y |
A |
||
|
|
|
|
|
|
|
||||
По двум известным точкам А и М составляем уравнение медианы АМ: A(−3, −2); M(10, 6)
x 3 |
|
y 2 |
|
x 3 |
|
y 2 |
|
10 3 |
6 2 |
13 |
8 |
||||
|
|
|
|||||
8(x 3) 13(y 2) |
|
|
|||||
8x 24 13y 26 |
|
|
|||||
8x − 13y − 2 = 0 − уравнение медианы AM
г) точку N пересечения медианы AM и высоты CH
Для нахождения координат точки N пересечения медианы АМ: 8x − 13y − 2 = 0 и высоты СН: 17x + 6y − 150 = 0 составляем систему уравнений и решаем
|
|
|
|
8x 2 |
|
|
|
|
|
8x 13y 2 0 |
y |
13 |
|
|
y |
8x 2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
6y 150 |
0 |
|
|
8x 2 |
|
13 |
||
17x |
|
|
|
|
|||||
|
|
|
6 |
|
150 0 |
|
0 |
||
|
|
|
17x |
|
221x 48x 12 1950 |
||||
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
8x 2 |
|
8 7,29 2 |
y 4,33 |
y |
|
y |
|
|
|
13 |
|
13 |
|
|
|
|
|
x 7,29 |
269x 1962 |
x 7,29 |
|
||
Получили точку N(7,29; 4,33) пересечения медианы AM и высоты CH
д) уравнение прямой, проходящей через вершину С параллельно стороне AB
Так как прямая, проходящая через вершину С, параллельна стороне АВ, то их угловые коэффициенты равны k1 176 .
Тогда, согласно уравнению y − yС = k1(x − xС), по точке C(6, 8) и угловому коэффициенту k1 составляем уравнение прямой проходящей через точку С:
y 8 176 (x 6) 17y 136 6x 36
6x 17y 36 136 0 6x 17y 100 0
е) расстояние от точки С до прямой AB
С(6, 8); 6x − 17y − 16 = 0 − уравнение стороны AB
Расстояние от точки С(xC; yC) до прямой АВ: Ax + By + C = 0 вычисляем по формуле
|
|
|
|
d |
Ax |
С |
By |
С |
C |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
A |
B |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
d CH |
6 6 ( 17) 8 16 |
|
36 136 16 |
|
116 |
6,44 |
|||||||||
6 |
2 |
( 17) |
2 |
|
|
325 |
|
|
18,02 |
||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. Решить следующие задачи.
2.2 Найти проекцию точки A(−8, 12) на прямую, проходящую через точки B(2, −3) и C(−5, 1).
Решение:
Найдем уравнение прямой, проходящей через точки B и C.
x x |
B |
|
|
y y |
B |
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
x |
|
x |
|
|
y |
|
y |
|
|
|
||||
C |
B |
|
C |
B |
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||
|
x 2 |
|
|
y 3 |
|
x 2 |
|
y 3 |
||||||
5 2 |
1 3 |
7 |
4 |
|||||||||||
|
|
|
|
|||||||||||
4 |
x 2 |
7 y 3 |
|
|
||||||||||
4x 8 7y 21 |
|
|
|
|||||||||||
4x 7y 13 0 |
|
|
|
|
||||||||||
Уравнение прямой, проходящей через данную точку A(−8, 12) перпендикулярно данному |
||||||||||||||
вектору |
|
|
|
|
|
|
|
|
|
|
A(x − xA) + B(y − yA) = 0 |
|||
n A; B BC xC x B ; yC yB 5 2; 1 ( 3) 7; 4

Значит, уравнение перпендикулярной прямой есть
7 x 8 4 y 12 0
7x 56 4y 48 0
7x 4y 104 0
Найдем точку пересечения прямых |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4x 7y 13 0 и |
7x 4y 104 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Решим систему уравнений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
4x 7y 13 0 |
|
4 |
4y 104 |
7y 13 0 |
16y 416 49y 91 0 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
4x 7y 13 0 |
|
|
|
4y 104 |
|
|
|
7 |
|
|
|
|
|
|
4y 104 |
|
||||||
|
|
|
|
|
x |
|
|
|
|
|
|
x |
||||||||||
7x |
4y 104 0 |
|
|
|
|
|
|
|
x |
4y 104 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
65y 325 |
|
|
y 5 |
|
y 5 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
4 5 104 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
4y 104 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x |
|
|
x |
|
|
|
|
|
x 12 |
|
|
|
|
|
|
|
|
|
||||
7 |
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Точка проекции имеет координаты A1(−12, 5)
Ответ: A1(−12, 5)
