лабораторная 224Д Вариант 1

БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра «Техническая физика»

Лаборатория «Электричество и магнетизм»

Отчет

по лабораторной работе №224д (вариант 1)

«Изучение характеристик и закономерностей электростатического поля на примере моделей, полученных на ЭВМ с графическим дисплеем»

Выполнил: студент гр. 10605120

Кекух А.А.

Проверил: Степанов М.А.

Минск 2021

1. Цель работы:

1) Изучить основные закономерности и характеристики электростатического поля;

2) Используя программу, получить на экране двумерную картинку силовых и эквипотенциальных линий поля, создаваемого двумя точечными зарядами.

3) Провести анализ моделей поля с различными начальными условиями.

2. Приборы и принадлежности: компьютерная программа.

3. Физическая модель:

1) Заряды точечные, неподвижные;

2) Заряды находятся в вакууме;

3) Посторонний полей нет;

4. Математическая модель:

1. Закон Кулона:

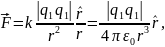
где 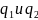– величины неподвижных точечных зарядов;

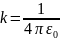– коэффициент пропорциональности;

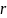– расстояние между зарядами;

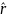– единичный вектор, проведенный от одного заряда к другому;

2. Напряженность поля точечного заряда:

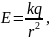
где – коэффициент пропорциональности;

– заряд, создающий поле;

– расстояние от заряда до точки, где рассчитывается напряженность;

3. Принцип суперпозиций электрических полей: если электрическое поле создается совокупностью точечных зарядов, то его напряженность равна векторной сумме напряженностей полей каждого заряда в отдельности.

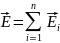
4. Потенциал поля точечного заряда:

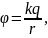
где – заряд, создающий поле;

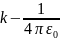– коэффициент пропорциональности;

– расстояние от заряда до точки, где рассчитывается потенциал;

5. Принцип суперпозиций для потенциалов: потенциал электрического поля системы зарядов равен алгебраической сумме потенциалов полей, созданных каждым из зарядов.

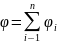
6. Поток напряженности:

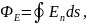
где 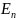– проекция вектора 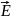на направление вектора нормали n.

7. Теорема Остроградского-Гаусса: полный поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, охватываемых этой поверхностью, деленной на .

,

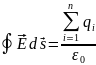где – полный поток вектора напряженности через произвольную замкнутую поверхность;

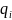– заряд, охватываемый этой поверхностью;

– диэлектрическая проницаемость;

5. Выполнение работы:

Задание 1а. Исследование поля диполя: .

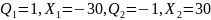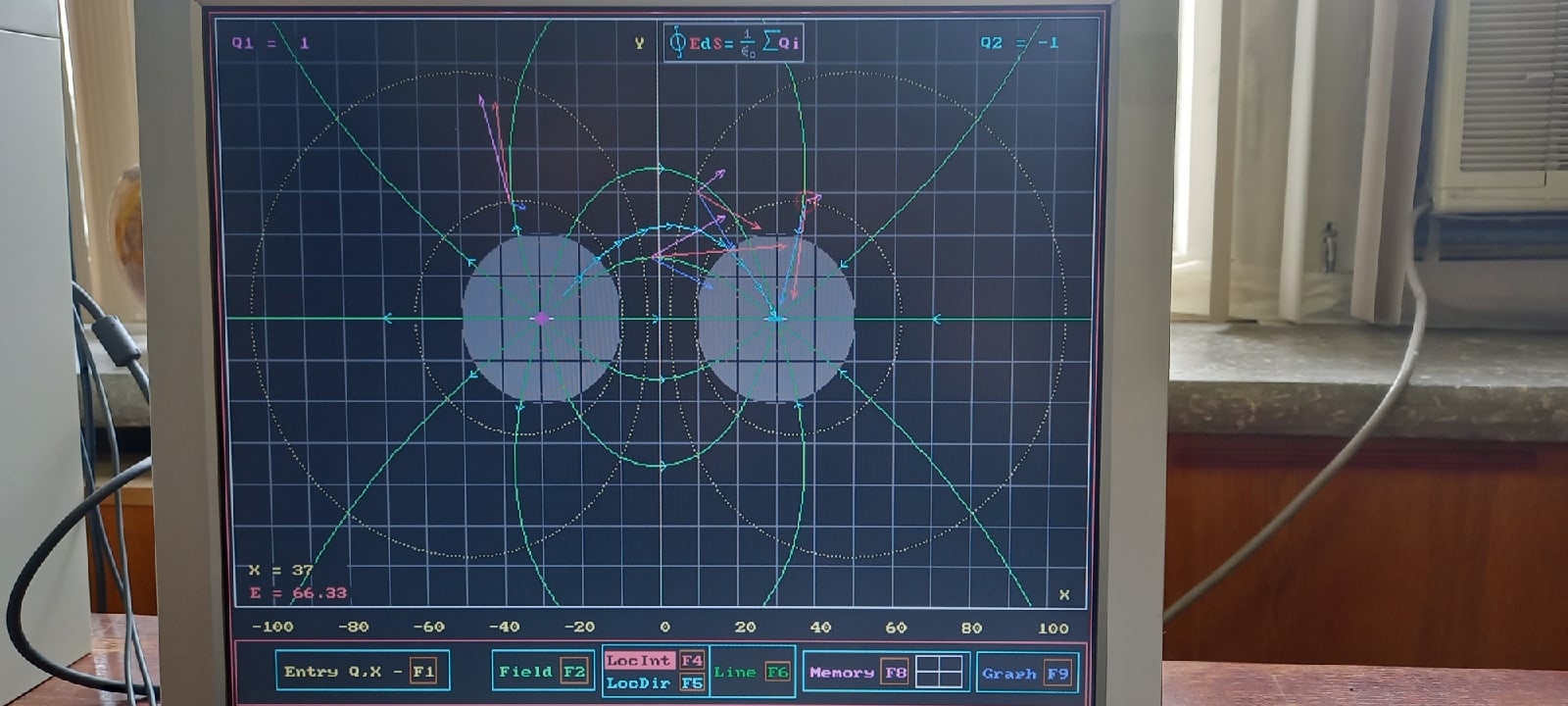
Суммарный поток через периметр равен нулю. Сумма зарядов внутри периметра равна нулю. Таким образов, теорема Остроградского-Гаусса подтверждена.

Задание 1б. Исследование картины поля, созданного двумя зарядами одного знака и одной величины: .

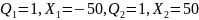Суммарный поток пропорционален 20 линиям, сумма зарядов равна 2.

Задание 2а. Исследование поля, созданного двумя зарядами знака, но разной величины: .

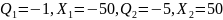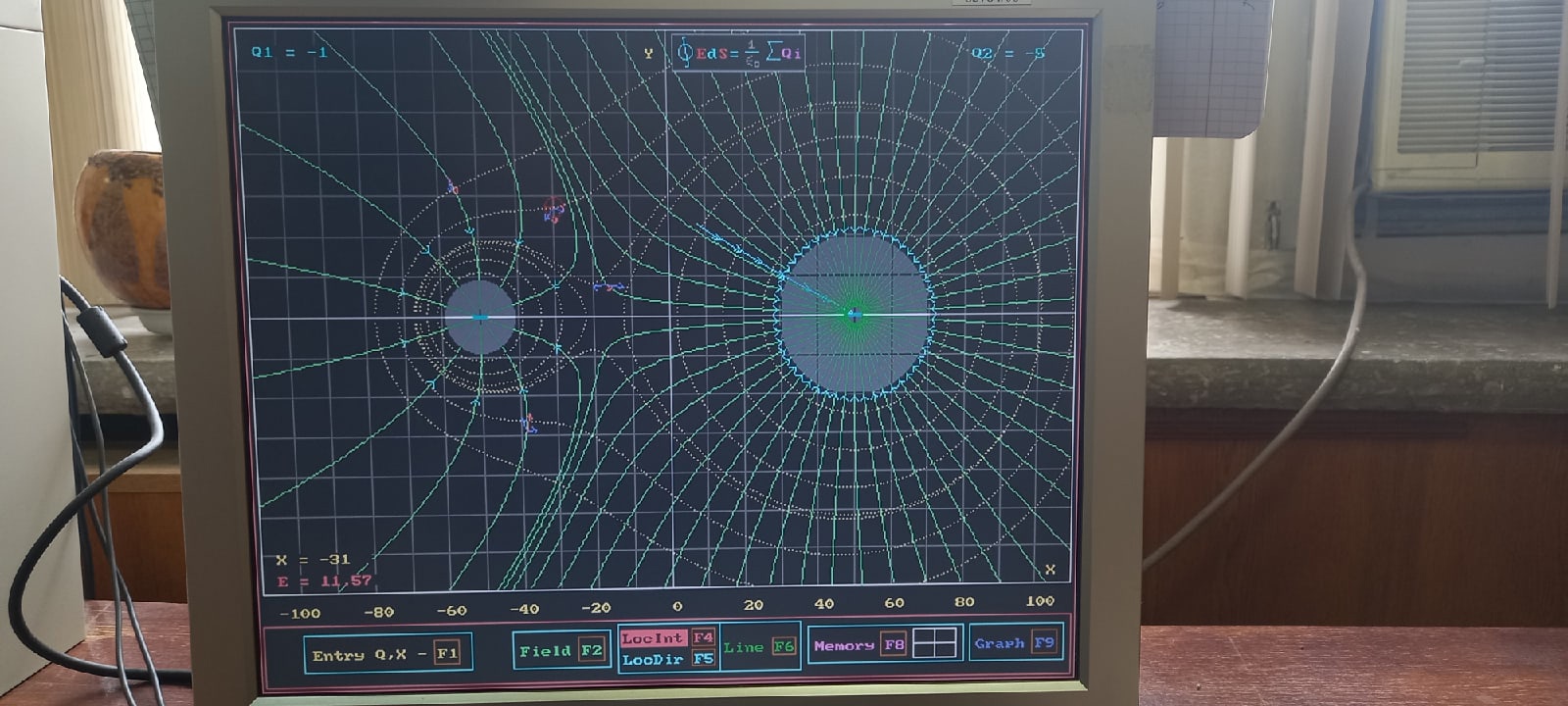
Суммарный поток пропорционален (-60), сумма зарядов равна (-6).

Задание 2б. Исследование поля, созданного двумя зарядами знака, но разной величины: .

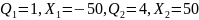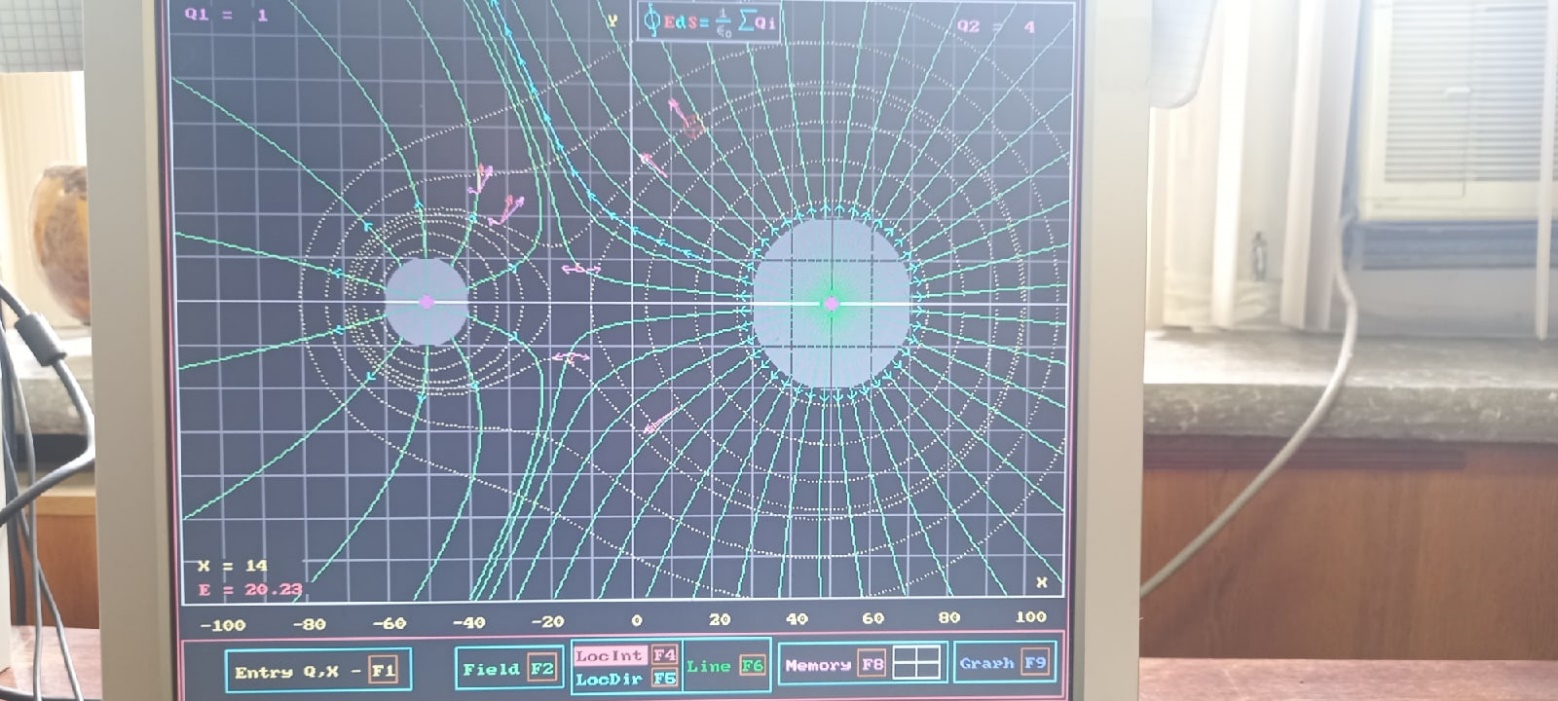
Суммарный поток пропорционален 50. Сумма зарядов равна 5.

Задание 3а. Исследование поля, созданного зарядами разных знаков и величин: .

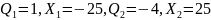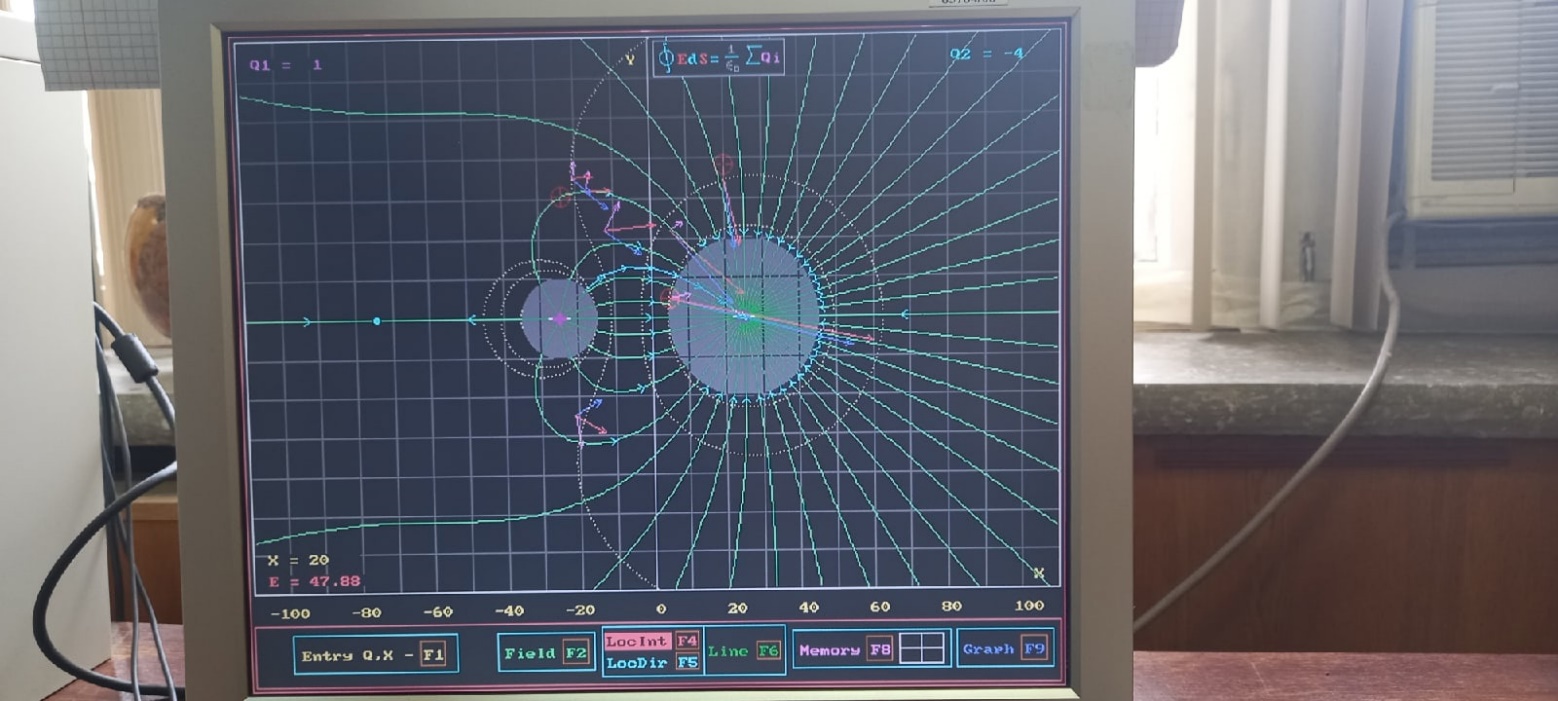
Суммарный поток пропорционален (-30). Сумма зарядов равна (-3).

Задание 3б. Исследование поля, созданного зарядами разных знаков и величин: .

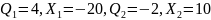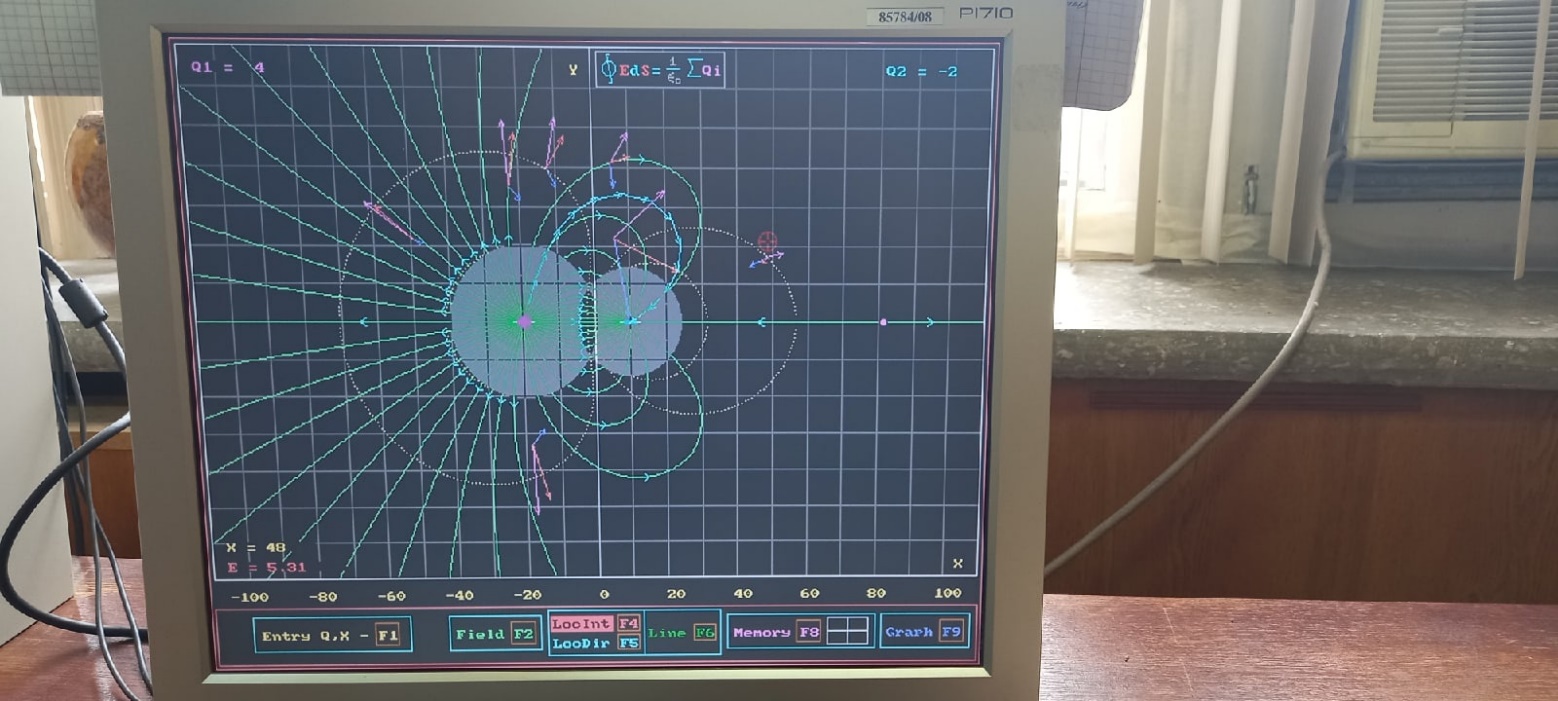
Суммарный поток пропорционален 20. Сумма зарядов равна 2.

6. Вывод:

Вектор напряженности поля, создаваемого положительны зарядом, всегда направлен от заряда, а вектор напряженности поля, создаваемого отрицательным зарядом, наоборот, направлен к заряду;

Чем дальше от заряда, тем поле слабее;

Силовая линия начинается на положительном, а заканчивается на отрицательном заряде;

Силовые линии направлены по касательной к вектору напряженности;

Очень большой отрицательный потенциал – в месте нахождения отрицательного заряда, очень большой положительный – в месте расположения положительного заряда, а с удалением от зарядов потенциал лежит где-то в бесконечности.