
4.3.6 Error diffusion halftoning
Screening as a task of digital image signal processing is the transformation of an array of multi-level samples into a binary one. Being distracted from the above-mentioned technological aspects related to the geometry of a resulting bitmap, dot shape, screen orientation, etc., this process can be considered stochastic and the resulting binary image must correspond to the original with the probability determined by the multilevel value of its sample. If the ink coverage on a unit print area of 16 x 16 microdots is defined by the 57th level of the eight-bit input sample, then the bitmap for this area should contain 57 units and 256 - 57 = 199 zeros. The same microdots number is formed within this area respectively dark and light.
Two-level quantization of multi-level values at a given threshold is accompanied by an error in the form of a difference between the quantized and threshold values. Redistribution (diffusion) of this error between the surrounding samples gave the name and formed the basis of one of the directions of obtaining pseudo-continuous images, a priori characterized by an irregular structure [4.13]. It does not use the above-described front set screen functions or alphabets, and the binary value bij (0 or 1) is assigned to the microdot as result of the original value aij and the threshold h comparison.
A relatively complex calculation procedure slows down the RIP operation and the method is often used only for computation and loading pre-defined alphabets in non periodic screening.
A simple algorithm to convert the eight-bit values aij in a binary bij for a given in advance threshold h entails the assignment of error dij to the following in bypass of a numeric array multi-level sample aij+1:
aij › h, then bij = 1, dij = aij-256;
aij ≤ h, then bij = 0, dij = aij;
aij+1 = aij + dij 4.1
These conditions show that if the threshold h is accepted, for example, 127, then the assignment bij = 1 is error-free only when the initial value aij = 255. For its smaller meanings (from 127 to 255), assigning "1" to a binary readout is redundant. Then the error dij is estimated as the difference aij-256 and is accounted by its addition to the value of a next sample aij+1.
Similarly, bij = 0 is true only when aij = 0. For all other values less than the threshold, it is insufficient and is compensated by adding this value itself as an error to the next sample.
As in other screening methods, it is necessary to satisfy a number of contradictory conditions and, in particular, the requirements of smooth tone rendition with the structure uniformity and high (adequate sampling rate of the original) definition of the resulting binary image.
To eliminate unwanted microdot clusters or directional structures (“worms”) in advanced error diffusion methods [4.14 - 4.17], the following measures are used:
error is spread over the neighboring pixels more evenly, bypassing them, for example, "serpentine" (from the beginning to the end of one line and from the end of the next to its beginning);
distribute the error not only to the next element but also to the neighboring ones, using weight coefficients that take into account their proximity to the given one, as shown in figure 4.18;
eliminate the periodicity in the error propagation by pseudo-random modifying the process, e.g., by adding a certain amount of "noise" to the threshold h or to the source values aij;
eliminate random microdot clusters and large blanks between them using so-called "binary search" [4.18] or low-frequency spatial filtering through the "blue mask" [4.19];
"pyramidal" error distribution in several stages with an intermediate forming its array for the entire image [4.20].
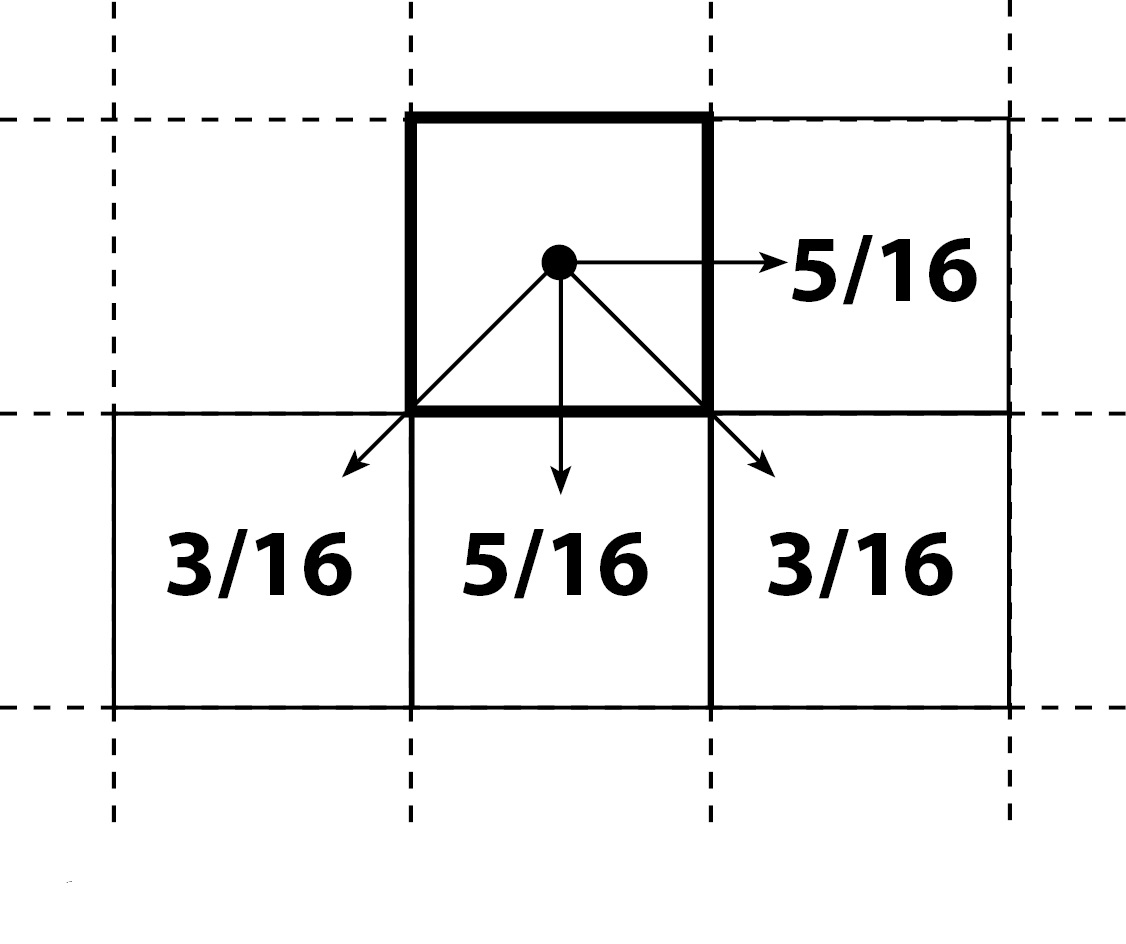
Figure 4.17. Example of the coefficients distribution for the two-level quantization error, taking into account the proximity (correlation) of the processed sample and its surround
These measures achieve, as a result, more uniform, and in light and dark colors almost regular arrangement of halftone dots. However, the more uniform diffusion achieved by such measures entails blurring of contours, lowering contrast of small details and other losses. Therefore, to improve the definition and sharpness, algorithms are also used of so-called "constrained averaging" with dynamic adjustment of the threshold, taking into account the adjustment sample value, local contrast, level and gradient of the optical parameter, etc.
Originally intended for reproduction in fine scan/fine print mode, error diffusion involves a sampling frequency of the original, which provides an independent multi-level tone value for each microdot of the future bitmap. Thanks to element-by-element tracking of the original tone changes, the print definition is not limited here by the screen ruling or the period of weight function. Therefore, with the same amount of data used, the sharpness and definition may be higher than in matrix methods.
In a more practical coarse scan / fine print mode of relatively "rough" reading, this method is implemented in conjunction with the interpolative multiplication of the values of the initial, rough samples for all recorded microdots [4.21].
