2 семестр / ИДЗ_пост_ток / Lektsia2

ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

Сила тока. Плотность тока.

Электрический ток есть упорядоченное движение электрических зарядов. В металлах и полупроводниках носителями тока являются электроны, в электролитах и ионизованных газах ― положительные и отрицательные ионы.

Электрический ток существует, если есть носители и электрическое поле. При включении электрического поля на хаотическое движение носителей со скоростью v накладывается упорядоченное движение со скоростью u (дрейфовой или упорядоченной). Таким образом, скорость носителей будет v + u. Так как среднее значение v (но не v) равно нулю, то средняя скорость носителей равна ‹ u ›.

Количественной характеристикой электрического тока служит величина заряда, переносимого через рассматриваемую поверхность в единицу времени. Её называет силой тока. Если за время dt через поверхность переносится заряд dq, то сила тока равна

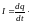(1)

За направление тока принимается направление, в котором перемещаются положительные носители. Единицей силы тока в системе СИ является а м п е р (А). Эта единица является основной в системе СИ и вводится на основании закона магнитного взаимодействия проводников с током.

Электрический ток может быть распределён по поверхности, через которую он течёт, неравномерно. Более детально ток можно охарактеризовать с помощью вектора плотности тока j. Этот вектор численно равен силе тока dI через расположенную в данной точке перпендикулярную к направлению движения носителей площадку , отнесённой к величине этой площадки:

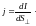₍₂₎

За направление j принимается направление вектора скорости u⁺ упорядоченного движения положительных носителей.

Поле вектора плотности тока можно изобразить с помощью линий тока, которые строятся так же, как линии тока в текущей жидкости, линии вектора Е и т.д.

Зная вектор плотности тока в каждой точке пространства можно найти силу тока I через любую поверхность S

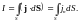(3)

Из (3) следует, что сила тока есть поток вектора плотности тока через поверхность.

Пусть в единице объёма содержится n⁺ положительных и n^– отрицательных носителей. Алгебраическая величина зарядов носителей равна соответственно e⁺ и e^–. Если под действием поля носители приобретают средние скорости u⁺ и u^–, то за единицу времени через единичную площадку пройдёт n⁺u⁺ положительных носителей, которые перенусут заряд e⁺n⁺u⁺. Аналогично отрицательные носители перенесут в противоположную сторону заряд e^–n^–u^–. Таким образом, для плотности тока получаем следующее выражение:

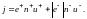₍₄₎

Этому выражению можно придать векторную форму:

₍₅₎

(оба слагаемых имеют одинаковое направление: вектор u^– направлен противоположно вектору j, при умножении его на отрицательный скаляр e^– получается вектор одинакового направления с j).

Ток, не изменяющийся со временем, называется постоянным. Для постоянного тока справедливо соотношение

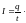(6)

Уравнение непрерывности.

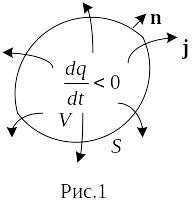Одним из фундаментальных физических законов является закон сохранения электрического заряда. Рассмотрим произвольную замкнутую неподвижную поверхность S (рис. 1). Интеграл 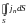должен равняться алгебраической сумме сил токов, проходящих через отдельные элементы dS этой поверхности, т.е. должен равняться количеству электричества, выходящего за единицу времени из ограниченного поверхностью объёма V (если n есть внешняя нормаль к S). В силу сохранения заряда эта величина должна быть равна скорости убывания заряда q, содержащегося в данном объёме:

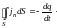(7)

Представив q в виде 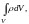получим соотношение

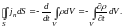(8)

Знак частной производной должен означать, что при дифференцировании по времени поверхность S и объём V считаются неподвижными. Преобразуем левую часть равенства (8) по теореме Остроградского ― Гаусса. В результате получим

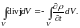(9)

Равенство (9) должно выполняться при произвольном выборе объёма V, по которому берутся интегралы. Это возможно лишь в том случае, если в каждой точке пространства выполняется условие

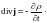(10)

Соотношение (10) называют уравнением непрерывности. Оно (равно как и уравнение (8)) выражает закон сохранения заряда. Согласно (10) в точках, которые являются источниками вектора j, происходит убывания заряда.

В случае постоянного тока 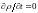. Следовательно, для постоянного тока уравнение (10) имеет вид

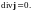(11)

Т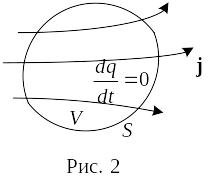 аким образом, в случае постоянного тока вектор j не имеет источников. Это означает, что линии тока нигде не начинаются и нигде не заканчиваются. Следовательно, линии постоянного тока всегда замкнуты. Соответственно 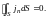Поэтому для постоянного тока картина, аналогичная изображённой на рис. 1, имеет вид, показанный на рис. 2.

Электрическое поле постоянных токов, как и поле электростатическое, является полем потенциальным. В частности, вектор напряжённости этого поля Е удовлетворяет условию 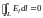и может быть выражен через градиент потенциала: 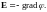Действительно, в поле постоянных токов распределение зарядов в пространстве должно оставаться стационарным, ибо если бы имело место какое бы то ни было перераспределение зарядов, то напряжённость поля неизбежно должна была бы измениться, и ток перестал бы быть постоянным. Но если распределение зарядов стационарно, то поле их должно быть тождественно с электростатическим полем соответственно распределённых неподвижных зарядов; то обстоятельство, что в данной точке пространства одни элементы заряда благодаря наличию тока сменяются другими, не может сказываться на напряжённости электрического поля, поскольку плотность зарядов в каждой точке пространства остаётся постоянной. Стало быть, стационарное поле постоянных токов, как и поле электростатическое, должно быть полем потенциальным.

Закон Ома.

Основной закон постоянного тока ― закон Ома, являющийся обобщением данных опыта, формулируется обычно следующим образом:

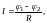(1)

где I ― сила тока в проводнике, R ― сопротивление определённого участка этого проводника, а φ₁ и φ₂ ― значения потенциала у начала и конца этого участка (считая по направлению тока).

Сопротивление в системе СИ измеряется в Омах. Проводник обладает по определению сопротивлением в 1 Ом, если при разности потенциалов на его концах в 1 Вольт по нему протекает ток силой в 1 Ампер. Сопротивление проводника зависит от его геометрических размеров, формы, материала и температуры. В частности, сопротивление проводника цилиндрической формы длиной l и сечением S вычисляется по формуле

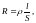(2)

где ρ ― удельное электрическое сопротивление, характеризующее вещество проводника. Если l = 1 и S = 1, то R численно равно ρ. В СИ ρ измеряется в ом-метрах (Ом·м).

Разность потенциалов (φ₁ – φ₂), входящую в формулу (1), можно выразить через линейный интеграл напряжённости поля Е, взятый от начального до конечного сечения рассматриваемого участка проводника:

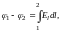(3)

где dl ― элемент длины проводника.

Линейный интеграл напряжённости электрического поля между точками 1 и 2 носит название напряжения, существующего между этими точками, и будет обозначаться через U₁₂:

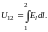(4)

Внося (3) и (4) в (1), получаем:

(5)

Эта форма закона Ома в случае постоянного электрического поля равносильна формуле (1). Однако она обладает тем преимуществом, что остаётся применимой и к переменным (квазистационарным) токам, тогда как в поле этих токов понятие электрического потенциала φ, а стало быть, и формула (1) оказываются неприменимыми.

Закон Ома в интегральной форме (1) связывает величины, относящиеся к разным точкам (φ₁ и φ₂) проводника. Выразим закон Ома в дифференциальной форме, устанавливающей связь между величинами, относящимися к одной определённой точке проводника. Рассмотрим какой-либо однородный по составу и цилиндрический по форме участок проводника. Внося выражение (2) в (5), получим:

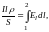
Или

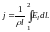
В случае постоянного тока в однородном цилиндрическом проводнике, ввиду тождества физических условий по всей его длине, слагающая поля по оси проводника 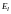, очевидно, имеет постоянное значение, так что

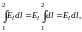
и, следовательно,

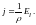
В каждой точке проводника направление тока совпадает с направлением электрического поля, обусловливающего движения зарядов. Стало быть, вектор плотности тока должен совпадать по направлению с вектором Е, и последнее уравнение может быть записано окончательно в виде

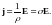(6)

Это уравнение, устанавливающее пропорциональность плотности тока в проводнике напряжённости поля в нём, представляет собою наиболее общую и простую формулировку закона Ома. Его можно назвать дифференциальной формой закона Ома (хотя в него и не входят производные), потому что оно устанавливает связь между величинами, относящимися к одной определённой точке проводника.

Хотя при выводе формулы (6) мы исходили из рассмотрения однородного цилиндрического проводника, однако в этой дифференциальной форме закон Ома оказывается применим к проводникам любой формы, как однородным, так и неоднородным.

Более того, уравнение (6) остаётся справедливым и в переменных электрических полях и, таким образом, является одним из основных уравнений электродинамики.

Фигурирующая в (6) обратная ρ величина σ называется удельной электрической проводимостью, или электропроводностью материала (не путать с σ ― поверхностной плотностью зарядов!). В системе СИ удельная электропроводность измеряется а Сименсах на метр (См/м) или Ом^–1·м^–1.

Электродвижущая сила. Закон Ома для неоднородного участка цепи.

Если в проводнике создать электрическое поле и не принять мер для его поддержания, то перемещение носителей тока быстро приведёт к тому , что поле внутри проводника изчезнет и ток прекратится. Для того чтобы поддерживать ток достаточно длительное время, нужно от конца проводника с меньшим потенциалом (носители тока предполагаются положительными) непрерывно отводить приносимые сюда током заряды, а к концу с большим потенциалом непрерывно их подводить. Иными словами, необходимо осуществить круговорот зарядов, при котором они двигались бы по замкнутому пути.

Циркуляция вектора напряжённости электростатического поля равна нулю. Поэтому в замкнутой цепи наряду с участками, на которых положительные носители движутся в сторону убывания потенциала φ, должны иметься участки, на которых перенос положительных зарядов происходит в направлении возрастании φ, т. е. против сил электростатического поля. Перемещение носителей на этих участках возможно лишь с помощью сил неэлектростатического происхождения, которые мы будем называть сторонними и будем обозначать напряжённость поля сторонних сил через Е^стр. К сторонним относятся силы, возникающие при соприкосновении проводников различного химического состава (гальванический элемент, аккумулятор) или различной температуры (термоэлемент) и т. д.

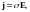Если под действием электростатического поля Е в проводнике возникает, согласно (6), ток плотности то под совокупным действием поля Е и поля сторонних сил Е^стр должен возникать, очевидно, ток плотности

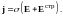(7)

Это выражение представляет собою дифференциальную форму обобщённого закона Ома, из которого нетрудно получить и интегральную форму этого закона.

Рассмотрим произвольный участок тока, заключённый между сечениями 1 и 2 и предположим, что в этом участке нет разветвлений цепи тока. Пусть сечение проводника равно S. Разделив уравнение (7) на σ, умножая, далее, это уравнение скалярно на элемент оси проводника dl, взятый по направлению тока j , и интегрируя от сечения 1 до сечения 2, получим (ввиду того, что (j· dl) = jdl):

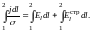
Заменив в первом интеграле j на 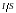и вынесем I как величину постоянную за знак интеграла. Далее, интеграл

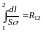
есть не что иное, как сопротивление участка проводника, лежащего между сечениями 1 и 2. Стало быть, окончательно:

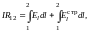(8)

что представляет собой наиболее общую интегральную форму обобщённого закона Ома.

Напряжение сторонних э.д.с. между точками 1 и 2

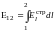(9)

называют электродвижущей силой, приложенной между этими точками. Внося (4) и (9) в (8), получим:

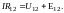(10)

Стало быть, произведение силы тока на сопротивление произвольного участка проводника равно сумме напряжения и сторонней э.д.с., приложенных к этому участку.

Если электрическое поле Е обладает потенциалом φ, то, согласно (3), последнее уравнение может быть записано так:

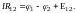(11)

Э.д.с., как и сила тока I, есть величина алгебраическая. В случае, когда э.д.с. способствует движению положительных носителей тока в выбранном направлении (в направлении 1―2), Е₁₂ > 0. Если э.д.с. препятствует движению положительных носителей в данном направлении, Е₁₂ < 0.

Если замкнутый ток лишён разветвлений, то выполняя в уравнении (8) интегрирование по всей длине этого тока, получим:

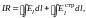(12)

где R ― полное сопротивление цепи. Если Е обладает потенциалом, то первый интеграл в (12) обращается в нуль, так что для постоянного тока (12) принимает вид:

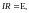(13)

где Е ― полная э.д.с. в цепи тока. Таким образом, приходим к школьной формулировке закона Ома для замкнутой цепи:

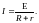(14)

Сила тока равна частному от деления э.д.с. на сумму сопротивлений нагрузки (R) и внутреннего сопротивления (r) источника.

Разветвлённые цепи. Правила Кирхгофа.

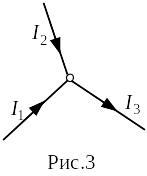Расчёт разветвлённых цепей значительно упрощается, если пользоваться правилами, сформулированными Кирхгофом. Этих правил два. Первое из них относится к узлам цепи. Узлом называется точка, в которой сходятся более чем два проводника (рис.). Ток, текущий к узлу, считается имеющим один знак (плюс или минус), текущий от узла ― имеющим другой знак (минус и плюс).

Первое правило Кирхгофа выражает закон сохранения заряда для постоянных токов и гласит, что алгебраическая сумма токов, сходящихся в узле, равна нулю:

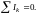(15)

Если бы это правило не соблюдалось, то в точках разветвления проводов накапливались бы электрические заряды, меняющиеся со временем и электрическое поле, а потому и токи не могли бы оставаться постоянными.

Уравнение (15) можно написать для каждого из n узлов цепи. Однако независимыми являются только n – 1 уравнение, n-е будет следствием из них.

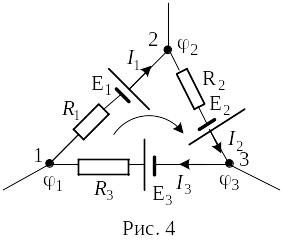Второе правило является следствием обобщённого закона Ома и относится к любому, выделенному в разветвлённой цепи замкнутому контуру (см., например, контур 1―2―3―1 на рис. 4). Выберем произвольно направление токов в каждом участке контура. Зададимся направлением обхода (например, по часовой стрелке, как указано на рисунке) и применим к каждому из неразветвлённых участков закон Ома:

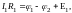
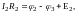
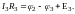
При сложении этих выражений потенциалы сокращаются и получается уравнение

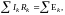(16)

которое выражает второе правило Кирхгофа: в любом замкнутом контре алгебраическая сумма произведений тика 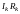равна алгебраической сумме э.д.с., приложенных к этому контуру.

Уравнение (16) может быть составлено для всех замкнутых контуров, которые можно выделить в данной разветвленной цепи. Однако независимыми будут только уравнения для тех контуров, которые нельзя получить наложением других контуров друг на друга. Иными словами, если можно выделить m контуров, то независимыми будут уравнения, составленные для m – 1 контура.

Под алгебраической суммой произведений понимается следующее. Если направление тока I_k совпадает с направлением обхода, то берётся о знаком «+», если направление тока I_k противоположно направлению обхода то перед в уравнении (16) ставится знак «–». Э.д.с. Е_k в правой части уравнения (16) берётся со знаком «+», если источник в направлении обхода проходится от «минусого» полюса к «плюсовому», и знак «–», если источник в направлении обхода проходится от «плюсового» полюса к «минусовому».

Мощность тока.

Рассмотрим произвольный участок цепи постоянного тока, к концам которого приложено напряжение U. За время t через каждое сечение проводника проходит заряд q = It. Это равносильно тому, что заряд It переносится за время t из одного конца проводника в другой. При этом силы электростатического поля и сторонние силы, действующие на данном участке, совершают работу

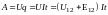(17)

(напомним, что напряжение U определяется как работа, совершаемая электростатическими и сторонними силами при перемещении единичного положительного заряда).

Разделив работу А на время t, за которое она совершается, получим мощность, развиваемую током на рассматриваемом участке цепи:

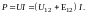(18)

Воспользовавшись законом Ома (10), получим

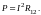(19)

В том случае, если поле Е обладает потенциалом φ, как это имеет место для поля постоянных токов, можно, согласно (3), записать уравнение (18) в виде

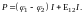(20)

Отношение мощности dР, развиваемой током в объёме проводника dV, к величине этого объёма называется удельной мощностью тока Р_уд, отвечающей данной точке проводника. По определению удельная мощность тока равна

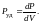(21)

Условно говоря, удельная мощность есть мощность, развиваемая в единице объёма проводника. Можно показать, что удельную мощность тока можно представить в виде

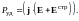(22)

Это выражение представляет собой дифференциальную форму интегрального выражения (18). (20).

Закон Джоуля ― Ленца.

В случае, когда проводник неподвижен и химических превращений в нём не совершается, работа тока (17) идёт на увеличение внутренней энергии проводника, в результате чего проводник нагревается. Принято говорить, что при протекании тока в проводнике выделяется тепло

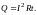(23)

Соотношение (23) было получено экспериментально Джоулем и, независимо от него, Ленцем и носит название закона Джоуля ― Ленца.

Если сила тока меняется со временем, то количество тепла, выделяющееся за время t, вычисляется по формуле

(24)

От формулы (23), определяющей тепло, выделяющееся во всём проводнике, можно перейти к выражению, характеризующему выделение тепла в различных точках проводника. Выделим в проводнике элементарный объём в виде цилиндра. Согласно закону Джоуля ― Ленца за время dt в этом объёме выделится тепло

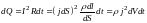(25)

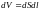( ― величина элементарного объёма).

Разделив выражение (25) на dV и dt, найдём количество тепла, выделяющееся в единице объема в единицу времени:

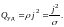(26)

По аналогии с наименованием величины (21), величину Q_уд можно назвать удельной тепловой мощностью тока

Уравнение (26) представляет собой наиболее общую формулировку закона Джоуля ― Ленца, применимую к любым проводникам, вне зависимости от формы, однородности и т. д., наконец, вне зависимости от того, имеем ли мы дело с постоянными или переменными токами.

11