4. Кратчайшие пути. Длина дуги. Алгоритм Флойда. Алгоритм Флойда-Уоршелла
Находит расстояние от каждой вершины до каждой за количество операций порядка n^3. Веса могут быть отрицательными, но у нас не может быть циклов с отрицательной суммой весов рёбер (иначе мы можем ходить по нему сколько душе угодно и каждый раз уменьшать сумму, так не интересно).
В массиве d[0… n — 1][0… n — 1] на i-ой итерации будем хранить ответ на исходную задачу с ограничением на то, что в качестве «пересадочных» в пути мы будем использовать вершины с номером строго меньше i — 1 (вершины нумеруем с нуля). Пусть идёт i-ая итерация, и мы хотим обновить массив до i + 1-ой. Для этого для каждой пары вершин просто попытаемся взять в качестве пересадочной i — 1-ую вершину, и если это улучшает ответ, то так и оставим. Всего сделаем n + 1 итерацию, после её завершения в качестве «пересадочных» мы сможем использовать любую, и массив d будет являться ответом.
n итераций по n итераций по n итераций, итого порядка n^3 операций.
Псевдокод:
прочитать g // g[0 ... n - 1][0 ... n - 1] - массив, в котором хранятся веса рёбер, g[i][j] = 2000000000, если ребра между i и j нет
d = g
for i = 1 ... n + 1
for j = 0 ... n - 1
for k = 0 ... n - 1
if d[j][k] > d[j][i - 1] + d[i - 1][k]
d[j][k] = d[j][i - 1] + d[i - 1][k]
вывести d
5. Бинарные деревья, основные понятия: дерево, корень, предок, потомок, лист, высота дерева, упорядоченное дерево.
Дерево – это структура данных, представляющая собой совокупность элементов и отношений, образующих иерархическую структуру этих элементов. Каждый элемент дерева называется вершиной (узлом) дерева. Вершины дерева соединены направленными дугами, которые называют ветвями дерева. Начальный узел дерева называют корнем дерева, ему соответствует нулевой уровень. Листьями дерева называют вершины, в которые входит одна ветвь и не выходит ни одной ветви.
Каждое дерево обладает следующими свойствами:
существует узел, в который не входит ни одной дуги (корень);
в каждую вершину, кроме корня, входит одна дуга.
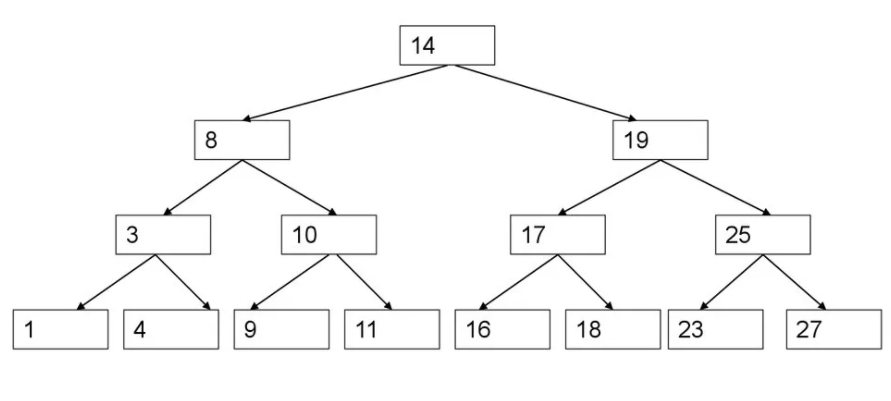
Упорядоченным называется дерево, в котором для каждого узла N значение левого дочернего узла меньше, чем значение в N, а значение правого дочернего узла больше значения в N.
узел – это точка, где может возникнуть ветвь. На рис.1 узлы – это, например, 70 и 200 и т.д;
корень – “верхний” узел дерева. Для дерева на рис.1 это узел 100;
ветвь – отрезок, описывающий связь между двумя узлами;
лист – узел, из которого не выходят ветви, т.е. не имеющий поддеревьев. На рис.1 это узлы 10, 90, 58, 65, 170, 210;
родительским (parent) – называется узел, который находится непосредственно над другим узлом;
дочерним – называется узел, который находится непосредственно под другим узлом;
предки данного узла – это все узлы на пути вверх от данного узла до корня. Например, предками узла 60 являются узлы 55, 50, 70, 100;
потомки – все узлы, расположенные ниже данного. Для узла 55 потомками являются узлы 60, 58, 65;
внутренний узел – узел, не являющийся листом;
порядок узла – количество его дочерних узлов;
глубина узла – количество его предков плюс единица;
глубина(высота) дерева –максимальная глубина всех узлов;
длина пути к узлу – количество ветвей, которые нужно пройти, чтобы дойти от корня к данному узлу;
длина пути дерева(длина внутреннего пути) – сумма длин путей всех его узлов.
6. AVL-деревья: узлы дерева, вставка узла в AVL-дерево.
АВЛ-дерево — это прежде всего двоичное дерево поиска, ключи которого удовлетворяют стандартному свойству: ключ любого узла дерева не меньше любого ключа в левом поддереве данного узла и не больше любого ключа в правом поддереве этого узла. Это значит, что для поиска нужного ключа в АВЛ-дереве можно использовать стандартный алгоритм. Для простоты дальнейшего изложения будем считать, что все ключи в дереве целочисленны и не повторяются.
Особенностью АВЛ-дерева является то, что оно является сбалансированным в следующем смысле: для любого узла дерева высота его правого поддерева отличается от высоты левого поддерева не более чем на единицу. Доказано, что этого свойства достаточно для того, чтобы высота дерева логарифмически зависела от числа его узлов: высота h АВЛ-дерева с n ключами лежит в диапазоне от log2(n + 1) до 1.44 log2(n + 2) − 0.328. А так как основные операции над двоичными деревьями поиска (поиск, вставка и удаление узлов) линейно зависят от его высоты, то получаем гарантированную логарифмическую зависимость времени работы этих алгоритмов от числа ключей, хранимых в дереве. Напомним, что рандомизированные деревья поиска обеспечивают сбалансированность только в вероятностном смысле: вероятность получения сильно несбалансированного дерева при больших n хотя и является пренебрежимо малой, но остается не равной нулю.
