Добавил:

kiruxa33 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Технический Университет им. Р.Е. Алексеева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Теоретические основы электротехники 4 семестр / Методичка ТОЭ часть вторая

.pdf

Скачиваний:

Добавлен:

01.09.2021

Размер:

3.32 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 117 8 9 10 11 > Следующая >>>

	на 2	рад. В соответствии с			данным
	ределением
	Длиной волны		называется
	ние между двумя ее ближайшими точ-
	ками,	различающимися		по	фазе	на
	2 рад. В соответствии с данным
	делением
	Длиной		волны	называется
	стояние между двумя ее ближайшими
	точками, различающимися по фазе на
	2 рад. В соответствии с данным
	делением

	Длиной волны		называется расстояние между двумя ее ближайшими точ-
ками, различающимися по фазе на 2						рад. В соответствии с данным определе-
нием
				(x	)	1		x 2	1,
откуда
							2

и с учетом (3.9)

VT Vf .

В соответствии с введенными понятиями прямой и обратной волн распределение напряжения вдоль линии в любой момент времени можно трактовать как результат наложения двух волн: прямой и обратной, перемещающихся вдоль линии с одинаковой фазовой скоростью, но в противоположных направлениях:

U	U пр U обр , (3.10) где в соот-
ветствии с (3.5) U пр		A e x и
		1
U обр	A2e x .
	(3.10) где в соответствии с (3.5)
U пр	A e x и U обр	A e x .
	1	2

		61

где в соответствии с (3.5) U пр	A e x	и U обр	A e x .
	1		2

Представление напряжения в виде суммы прямой и обратной волн согласно (3.10) означает, что положительные направления напряжения для обеих волн выбраны одинаково: от верхнего провода к нижнему.

Аналогично для тока на основании (3.6) можно записать

I пр

I обр , (3.11) где

I пр

A e

x / Z

и I обр

A e x

/ Z

(3.11) где I пр

A e

x / Z

I обр

A e x / Z

где I пр

A e

x / Z

и I обр

A e x / Z

Положительные направления прямой и обратной волн тока в соответствии с (11) различны: положительное направление прямой волны совпадает с положительным направлением тока I (от начала к концу линии), а положительное направление обратной волны ему противоположно.

На основании (3.10) и (3.11) для прямых и обратных волн напряжения и тока выполняется закон Ома:

I пр	U пр		;	I обр	U обр
I пр			;	I обр
		Zс			Zс

3.2. Бесконечно длинная однородная линия. Согласованный режим работы

В случае бесконечно длинной линии в выражениях (3.5) и (3.6) для напря-

жения и тока слагаемые, содержащие e x , должны отсутствовать, так как стремление x 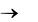лишает эти составляющие физического смысла.

Следовательно, в рассматриваемом случае A2 0 . Таким образом, в решении уравнений линии бесконечной длины отсутствуют обратные волны тока и напряжения. В соответствии с вышесказанным

	A e		x
U A e x , I	1			.


1		ZC
		ZC

(3.12) На основании соотношений (3.12) можно сделать важный вывод, что для бесконечно длинной линии в

любой ее точке, в том числе и на входе, отношение комплексов напряжения и тока есть постоянная величина, равная волновому сопротивлению:

На основании соотношений (3.12) можно сделать важный вывод, что для бесконечно длинной линии в любой ее точке, в том числе и на входе, отношение комплексов напряжения и тока есть постоянная величина, равная волновому сопротивлению:

Zс Zвх .

Таким образом, если такую линию мысленно рассечь в любом месте и вместо откинутой бесконечно длинной части подключить сопротивление, численно равное волновому, то режим работы оставшегося участка конечной длины не изменится. Отсюда можно сделать два вывода:

-уравнения бесконечно длинной линии распространяются на линию конечной длины, нагруженную на сопротивление, равное волновому. В этом случае также имеют место только прямые волны напряжения и тока;

-у линии, нагруженной на волновое сопротивление, входное сопротивление также равно волновому.

Режим работы длинной линии, нагруженной на сопротивление, равное волновому, называется согласованным, а сама линия называется линией с со-

гласованной нагрузкой.

Отметим, что данный режим практически важен для передачи информации, поскольку характеризуется отсутствием отраженных (обратных) волн, обусловливающих помехи.

Согласованная нагрузка полностью поглощает мощность волны, достигшей конца линии. Эта мощность называется натуральной. Поскольку в любом

сечении согласованной линии сопротивление равно волновому, угол сдвига между напряжением и током неизменен. Таким образом, если мощность, по-

лучаемая линией от генератора, равна P	U I	1	cos , то мощность в конце ли-
1	1	1

ний длиной l в данном случае

P	U	I	2	cos	U e			l I e		l cos Pe 2 l ,
2	2		2			1		1		1
откуда КПД линии
						P2		e 2		l
						P		e 2
						P
						1
и затухание
					l		1	ln	P2	.
					l	2		ln	P	.
						2			P
								1

Как указывалось при рассмотрении четырехполюсников, единицей затуха-

ния является непер, соответствующий затуханию по мощности в e2 раз, а по напряжению или току – в e раз.

3.3. Линия без искажений Пусть сигнал, который требуется передать без искажений по линии, является ческим, т.е. его можно разложить в ряд Фурье. Сигнал будет искажаться, если для составляющих его гармонических затухание и фазовая скорость различны, т.е. если последние являются ми частоты. Таким образом, для ствия искажений, что очень важно, например, в линиях передачи ции, необходимо, чтобы все гармоники распространялись с одинаковой стью и одинаковым затуханием, скольку только в этом случае, шись, они образуют в конце линии нал, подобный входному.

Пусть сигнал, который требуется передать без искажений по линии, является периодическим, т.е. его можно разложить в ряд Фурье. Сигнал будет искажаться, если для составляющих его гармонических затухание и фазовая скорость различны, т.е. если последние являются функциями частоты. Таким образом, для отсутствия искажений, что очень важно, например, в линиях передачи информации, необходимо, чтобы все гармоники распространялись с одинаковой скоростью и одинаковым затуханием, поскольку только в этом случае,

сложившись, они образуют в конце линии сигнал, подобный входному. Идеальным в этом случае является так называемая линия без потерь, у

которой сопротивление R0 и проводимость g0 равны нулю. Действительно, в этом случае

Z0Y0

j L0 j C0 j L0C0

j ,

т.е. независимо от частоты коэффициент затухания

const и фазовая ско-

рость

const .

L0C0

Однако искажения могут отсутствовать и в линии с потерями. Условие передачи сигналов без искажения вытекает из совместного рассмотрения выражений для постоянной распространения:

Z0 Y0 ZC Y0

ZC g0 j ZCC0

(3.13)

и фазовой скорости:

(3.14)

C0 ZC

Из (3.13) и (3.14) вытекает, что для получения

const и V

const , что обес-

печивает отсутствие искажений, необходимо, чтобы ZC const , т.е. чтобы волновое сопротивление не зависело от частоты.

j L0

R0 / L0

(3.15)

j C0

g0 / C0

Как показывает анализ (3), при

R0	g0	(3.16)
L0	C0


ZC	L0 / C0 есть вещественная константа.

Линия, параметры которой удовлетворяют условию (3.16), называется линией без искажений. Фазовая скорость для такой линии

C0 ZC

L0C0

и затухание

R g

Следует отметить, что у

реальных

линий

(и воздушных, и кабельных)

V R0 / L0 g0 / C0 . Поэтому для придания реальным линиям свойств линий

без искажения искусственно увеличивают их индуктивность путем включения через одинаковые интервалы специальных катушек индуктивности, а в случае кабельных линий – также за счет обвивания их жил ферромагнитной лентой.

3.4. Уравнения линии конечной длины

Постоянные A1 и A2 в полученных в предыдущей лекции формулах

				x		x	(3.17)
U		A1e			A2e ;		(3.17)
U		A1e			A2e ;

I	1		( A1e x			A2e x )	(3.18)
I			( A1e x			A2e x )	(3.18)
	ZC
	ZC

определяются на основании граничных условий.

Пусть для линии длиной l (см. рис. 3.1) заданы напряжение U и ток I в начале линии, т.е. при x 0 .Тогда из (3.17) и (3.18) получаем

A2 ;

I1 ZC A1

A2 ,

откуда

);

Z H

x' l

Рис. 3.3

Подставив найденные выражения A1

и A2

в (3.5) и (3.6), получим

I 1

ZC )e

(U 1

I 1 ZC )e x

U 1 1

(e x

e x )

(3.19)

ZC 1

I 1

(e x

e x ) U 1 chγx I 1 ZCshγx,

(U 1

I 1

ZC )e

I 1 ZC )e

U 1

)

2ZC

(3.20)

I 1

)

U 1

shγx I 1

chγx.

Уравнения (3.19) и (3.20) позволяют определить ток и напряжение в любой

точке линии по их известным значениям в начале линии. Обычно в практиче-

ских задачах бывают заданы напряжениеU 2 и ток I 2 в конце линии. Для выражения напряжения и тока в линии через эти величины перепишем уравнения (5) и (6) в виде

A1e (l

x ')

A2e (l x ') ;

(3.21)

A1e

x ')

A2 e (l x ') .

(3.22)

l и B

Обозначив B

A e

A e l из уравнений (3.21) и (3.22) при x'

0, полу-

чим

U 2

B2 ,

I 2 ZC

B2 ,

откуда

B	1		(U		I		Z				),
				2		2			C
1	2

B		1	(U		I			Z			).
				2		2				C
2	2

После подстановки найденных выражений B1 и B2 в (3.21) и (3.22) полу-

чаем уравнения, позволяющие определить ток и напряжение по их значениям в конце линии:


U	U 2 chγ(l			x)	I 2 ZCshγ(l	x);	(3.23)
	U 2						(3.24)
I	U 2		shγ(l	x)	I 2 chγ(l	x) .
I			shγ(l	x)	I 2 chγ(l	x) .
		ZC

3.5.Уравнения длинной линии как четырехполюсника

Всоответствии с (3.23) и (3.24) напряжения и токи в начале и в конце линии связаны между собой соотношениями


U 1	U 2 ch l I 2 ZC sh l;
		U 2
I 1		U 2		sh l I 2 ch l .
I 1				sh l I 2 ch l .
			ZC

Эти уравнения соответствуют уравнениям симметричного четырехполюсника, коэффициенты которого A D chγl ; B ZCshγl и C shγl / ZC ; при этом усло-

вие A D ch2γl sh2γl 1 выполняется.

Указанное означает, что к длинным линиям могут быть применены элементы теории четырехполюсников, и, следовательно, как всякий симметричный четырехполюсник, длинная линия может быть представлена симметричной Т- или П- образной схемами замещения.

3.6. Определение параметров длинной линии из опытов холостого хода и короткого замыкания

Как и у четырехполюсников, параметры длинной линии могут быть определены из опытов холостого хода (ХХ) и короткого замыкания (КЗ).

При ХХ U l хх U 2 chγl и I l хх U 2 shγl / ZC , откуда входное сопротивление

Zвх хх

U l хх

ZCcth l .

(3.25)

I l хх

При КЗ U l кз I 2 ZCshγl и

I l кз

I 2 chγl . Следовательно,

Zвх кз

U l кз

ZC th l .

(3.26)

I l кз

На основании (3.25) и (3.26)

Zвх. хх Zвх. кз

(3.27)

th 2

Zвх. кз

Zвх. хх

откуда

Zвх. кз

Zвх. хх

γl

Arcth

Zвх. кз

(3.28)

Zвх. хх

Zвх. кз

Zвх. хх

Выражения (3.27) и (3.28) на основании данных эксперимента позволяют

определить вторичные параметры ZC

и линии, по которым затем могут быть

рассчитаны ее первичные параметры R0 , L0 , g0 иC0 .

3.7. Линия без потерь

Линией без потерь называется линия, у которой первичные параметры R0 и g0 равны нулю. В этом случае, как было показано ранее,

0 иL0C0 . Таким образом,

j j	j	2	j	2	,

V		VT

откуда l j2 l / .

Раскроем гиперболические функции от комплексного аргумента l l j l :

ch(	l	j	l)	ch	l	cos	l	jsh	l	sin	l,
sh(	l	j	l)	sh	l	cos	l	jch	l	sin	l.

Тогда для линии без потерь, т.е. при 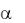0 , имеют место соотношения:

ch (l x) cos 2 (l x) и sh (l x) j sin 2 (l x) .

Таким образом, уравнения длинной линии в гиперболических функциях от комплексного аргумента для линии без потерь трансформируются в уравнения, записанные с использованием круговых тригонометрических функций от вещественного аргумента:

U 2 cos

j I 2 ZC sin

(l x) ;

(3.29)

U 2

x) .

(3.30)

j ZC sin

(l x)

I 2 cos (l

Строго говоря, линия без потерь (цепь с распределенными параметрами без потерь) представляет собой идеализированный случай. Однако при выполнении R0 /( L0 ) 1 и g0 /( C0 ) 1, что имеет место, например, для высоко-

частотных цепей, линию можно считать линией без потерь и, следовательно, описывать ее уравнениями (3.29) и (3.30).

3.8. Стоячие волны в длинных линиях

Как было показано выше, решение уравнений длинной линии можно представить в виде суммы прямой и обратной волн. В результате их наложения в цепях с распределенными параметрами возникают стоячие волны.Рассмотрим два предельных случая: ХХ и КЗ в линии без потерь, когда поглощаемая приемником активная мощность равна нулю. При ХХ на основании уравнений

(3.29) и (3.30) имеем

U U 2 cos	2	x'	и I j	U 2	sin	2	x' ,
				ZC

откуда для мгновенных значений напряжения и тока можно записать:

u(x',t)

U 2m sin

cos

U 2m

sin

U 2m

sin

x' ,

(3.31)

u(x',t)

U 2m

cos

sin

U 2m

sin

U 2m

sin

x' .

(3.32)

2ZC

Последние уравнения представляют собой уравнения стоячих волн, являющихся результатом наложения прямой и обратной волн с одинаковыми амплитудами.

<<< < Предыдущая 1 2 3 4 5 67 / 117 8 9 10 11 > Следующая >>>