ВОПРОСЫ К ЭКЗАМЕНАЦИОННЫМ БИЛЕТАМ ПО ДИСЦИПЛИНЕ

«МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ТЕХНИЧЕСКИХ ОБЪЕКТОВ»

1. Раскройте понятие математической модели и перечислите её основные свойства.

Математическая модель – эквивалент объекта, выражаемый в математической форме. Его можно выразить в форме.

Математическая модель строится в 3 этапа:

1. Строится математический «эквивалент», отражающий главные свойства объекта. Математическая модель, в отличие от реального объекта, может быть исследована теоретическими методами.

2. Разработка алгоритма, реализующего методы исследования.

3. Разработка программ, реализующих алгоритм.

Свойства математических моделей:

1. Множественность и единство моделей (первое – возможность детализации объекта; второе – говорит о том, что вся детализация соответствует одному и тому же объекту);

2. Универсальность модели (одной и той же моделью могут быть описаны совершенно разные объекты);

3. Конечность (то насколько ММ детализована)

4. Адекватность моделей (степенью соответствия свойств и параметров модели свойствам и параметрам реального объекта);

5. Эффективность моделей (практическая полезность модели);

6. Свойство достаточной простоты (свойство предполагает собой, что в ММ охвачены только необходимые для исследования характеристики объекта);

7. Устойчивость модели (отражает реакцию модели на возмущающие факторы).

2. Раскройте понятие рабочей точки прибора с нелинейной вах (на примере полупроводникового диода). Изложите основные методы численного решения нелинейного уравнения.

Рабочая точка прибора – точка на плоскости входных или выходных характеристик усилительного прибора, связывающая текущие значения напряжений и токов в нём.

Например, рассмотрим цепь с диодом:

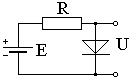
Падение напряжения на диоде можно найти из ММ диода и цепи:

Оба уравнения можно представить в виде графика. Точка их пересечения будет рабочей точкой:

Численные методы решения нелинейного уравнения:

1. Метод итераций/Метод последовательных приближений: метод заключается в последовательной подстановке результата в зависимость . За можно взять например примерное значение, полученное из графического решения. Критерием окончания численного расчёта является получение решения с заданной точностью в выражении . Недостатком метода является то, что он работает только при .

2. Метод касательных (Метод Ньютона-Гарсона): в данном методе решения нелинейных уравнений мы подставляем получаемые результаты в формулу . Таким образом мы проводим касательные к графику через точку с координатой , определяем , где она пересечет ось абсцисс в точке и повторяем тот же алгоритм для . Делаем так до заданного приближения.

3. Метод половинного деления: в данном методе мы выбираем отрезок , такой что а так же соответствующий критерию изменения знака , делим его пополам и выбираем ту половину, в которой меняет знак: . В итоге мы получаем семейство вложенных друг в друга уменьшающихся отрезков, так что существует предел, являющийся ответом. Критерий остановки: .

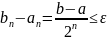4. Метод хорд (Метод пропорциональных частей) : метод похож на предыдущий. Мы проводим хорду на некотором отрезке, смотрим, где в какой точке хорда пересекла ось абсцисс, берем ту часть отрезка, в котором функция меняет знак и повторяем алгоритм. Уравнение приближения по этому методу: . При чем возможны два случая: