Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное

учреждение высшего образования

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ

УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра промышленной электроники (ПрЭ)

Экзаменационное задание

по дисциплине «Методы анализа и расчета электронных схем»

Вариант 51

	Выполнил
	студент гр. з-66
	________ П.В. Шерстюк
	«13» мая 2020 г.

2020

Задание

Для заданной электронной схемы сформировать матрицу эквивалентных сопротивлений или проводимостей (в зависимости от заданного координатного базиса) методом эквивалентных схем в матричной форме и записать выражение для заданной схемной функции.

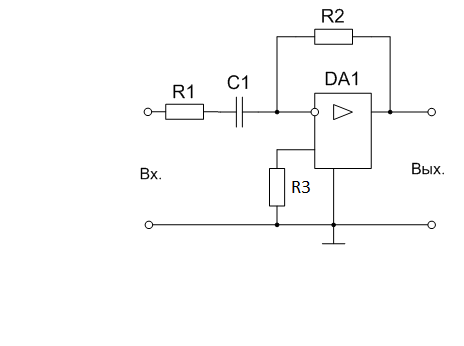
Рисунок 1 – Схема исследуемого усилителя

Решение

1. При составлении схемы замещения по переменному току источник входного сигнала в схеме замещения по переменному току представляем ветвью, содержащей параллельно включенные идеальный источник переменного тока и внутреннюю проводимость .

Для формирования математической модели в полном диапазоне частот в схеме замещения по переменному току учитываются все реактивные компоненты исходной схемы.

Нагрузка в схеме замещения по переменному току представлена ветвью с проводимостью .

Схема замещения по переменному току для полного диапазона частот представлена на рис. 2.

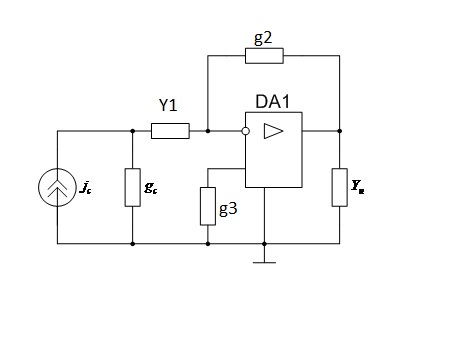
Рисунок 2 – Схема замещения по переменному току

для полного диапазона частот

2. Для реализации метода эквивалентных схем операционный усилитель в схеме замещения заменяется эквивалентной схемой (рис. 3).

Рисунок 3 – Линейная малосигнальная высокочастотная

физическая эквивалентная схема ОУ

В эквивалентной схеме – входная проводимость для дифференциального сигнала, , – входные проводимости для синфазного сигнала, – выходная проводимость, – коэффициент усиления при разомкнутой ОС.

Замещая операционный усилитель эквивалентной схемой, получим схему замещения, содержащую только двухполюсные -компоненты (рис. 4).

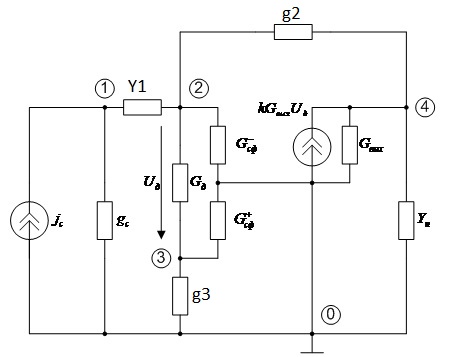
Рисунок 4 – Схема замещения, содержащая только

двухполюсные компоненты

Схема замещения содержит узлов, поэтому система независимых сечений содержит сечения. Выберем каноническую систему сечений, для чего в схеме замещения выбран базисный узел и пронумерованы остальные узлы.

Порядок укороченной матрицы проводимостей равен . Главную диагональ матрицы заполняем собственными проводимостями соответствующих узлов, а недиагональные элементы – взаимными проводимостями, взятыми со знаком «минус». Зависимый источник включен между базисным узлом и узлом 4, а его управляющее напряжение действует между узлами 2 и 3. Поэтому управляющая проводимость добавляется к элементам укороченной матрицы проводимостей, расположенным на пересечении 4 строки и 2 и 3 столбцов. Зависимый источник направлен к узлу 4, а управляющее напряжение – от узла 2 к узлу 3, следовательно, при добавлении к элементу матрицы знак управляющей проводимости не изменится, а при добавлении к элементу – изменится на противоположный. В результате укороченная матрица проводимостей принимает вид:

.

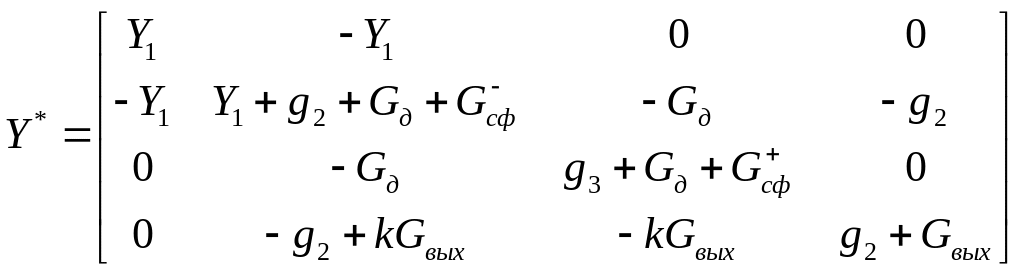3. Выражение схемной функции коэффициента передачи тока:

.

Для выбранной системы сечений , , поэтому

Список использованных источников

1. Легостаев Н. С. Методы анализа и расчета электронных схем : учебное пособие / Н. С.Легостаев, К. В. Четвергов. – Томск : Эль Контент, 2013. – 158 с.

2. Легостаев Н. С., Четвергов К. В. Методы анализа и расчета электронных схем : Учебное методическое пособие. – Томск : Томский межвузовский центр дистанционного образования, 2007. – 105 с.