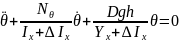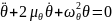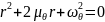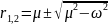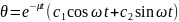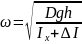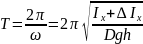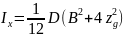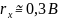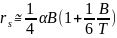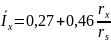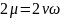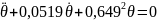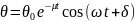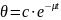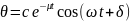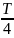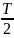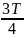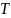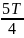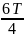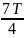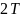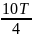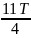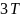МИНЕСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОЛВАТЕЛДЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗРОВАНИЯ
«НИЖЕГОРОДСКИЙ ГОСУДАРТТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. Р.Е. АЛЕКСЕЕВА» НГТУ
Кафедра «Кораблестроение и авиационная техника»
Расчётно-графическая работа
По дисциплине «Основы кораблестроения»
Расчет качки судна
Выполнил Угулава Р.Г.
Группа 17-КС-1
Проверил Зуев В.А.
Нижний Новгород, 2020
Содержание
Y
Введение 2
1 Бортовая качка судна без хода с учетом сопротивлений 3
2 Расчет вынужденной бортовой качки судна 8
3 Влияние курсового угла и скорости хода на бортовую качку судна 12
Список литературы 15
Введение
В пояснительной записке приведен расчет свободных и вынужденных бортовых колебаний корабля, сделаны выводы о влиянии качки.
1 Бортовая качка судна без хода с учетом сопротивлений
В начале рассмотрим свободные бортовые колебания корабля, уравнение которого записывается в виде:
|
|
(1) |
где
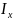 – момент
инерции массы корпуса корабля относительно
центральной продольной оси судна;
– момент
инерции массы корпуса корабля относительно
центральной продольной оси судна;
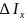 – момент
инерции присоединённой массы воды
относительно той же оси;
– момент
инерции присоединённой массы воды
относительно той же оси;
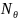 – сопротивление воды при качке корабля;
– сопротивление воды при качке корабля;
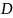 –
водоизмещение судна в тоннах;
–
водоизмещение судна в тоннах;
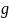 – ускорение свободного падения равное
9,81 м/с2;
– ускорение свободного падения равное
9,81 м/с2;
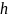 -
поперечная метацентрическая высота;
-
поперечная метацентрическая высота;
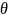 –
угловое перемещение судна (крен);
–
угловое перемещение судна (крен);
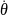 –
угловая скорость при качке,
–
угловая скорость при качке,
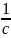 ;
;
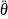 – угловое
ускорение при бортовой качке,
– угловое
ускорение при бортовой качке,
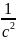 .
.
Поскольку качка свободная и возмущающих сил нет, то поэтому в правой части уравнения стоит нуль.
Это линейное дифференциальное уравнение II-го порядка с постоянными коэффициентами и с нулевой правой частью. Для его решения запишем каноничную форму этого уравнения, разделив его на коэффициент при старшей производной:
|
|
(2) |
где

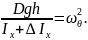
Индексы обозначает, что член принадлежит к бортовой качке и в дальнейшем упустим его. Таким образом уравнение запишется в виде:
|
|
(3) |
Для его решения запишем характеристическое уравнение:
|
|
(4) |
Это алгебраическое уравнение II-го порядка, которое имеет следующее решение:
|
|
|
Поскольку
в большинстве случаев
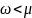 ,
то подкоренное выражение будет мнимым
и в
этом
случае получим пару комплексно-сопряженных
корней этого уравнения. Как известно
из теории решения дифференциальных
уравнений, его общее решение можно
записать в виде:
,
то подкоренное выражение будет мнимым
и в
этом
случае получим пару комплексно-сопряженных
корней этого уравнения. Как известно
из теории решения дифференциальных
уравнений, его общее решение можно
записать в виде:
|
|
(5) |
где
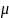 –
коэффициент сопротивления при бортовой
качке;
–
коэффициент сопротивления при бортовой
качке;
 – частота свободных бортовых колебаний
и будет равна,
:
– частота свободных бортовых колебаний
и будет равна,
:
|
|
(6) |
Период колебаний будет определяться по формуле, c:
|
|
(7) |
При заданном водоизмещении, чем больше поперечная метацентрическая высота (выгодное с точки зрения увеличения остойчивости) приводит к уменьшению периода качки, то есть она становится резкой и порывистой. Таким образом поставленная задача состоит в определении частоты и периода свободных колебаний и в определенных закона этих колебаний во времени, вычисление коэффициентов в уравнении можно выполнить с использованием приближенных формул, полученных по экспериментальным данным.
Момент инерции массы судна относительно центральной оси определяется по формуле Дуайера:
|
|
(8) |
где
– водоизмещение
судна в тоннах;
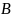 – ширина судна, м;
– ширина судна, м;
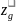 - аппликата
метацентрической высоты.
- аппликата
метацентрической высоты.
Подставив значение в уравнение получим:
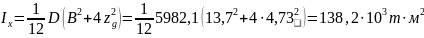
Момент инерции присоединённой массы воды зависит от радиуса инерции судна и от среднего плеча смоченной поверхности соответственно и определяются по формулам:
|
|
(9) (10) |
Безразмерный момент инерции массы воды определяется по формуле:
|
|
(11) |
Таким образом получим:
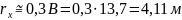
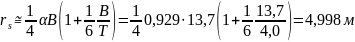
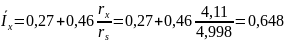
В этом случае момент инерции присоединённой массы воды определяется так:
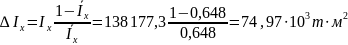
Тогда:
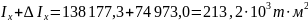
Коэффициент сопротивления при бортовой качке определяется по формуле:
|
|
(12) |
где
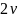 – влияние
скуловых килей на сопротивление качки
(
– влияние
скуловых килей на сопротивление качки
(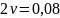 ,
если скуловых килей не имеется и
,
если скуловых килей не имеется и
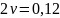 ,
если
кили есть. Так как на проектируемом
судне скуловые кили не предусматриваются,
то примем
).
,
если
кили есть. Так как на проектируемом
судне скуловые кили не предусматриваются,
то примем
).
Определение частоты свободных колебаний судна по формуле (6):
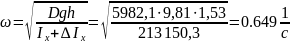
Период по формуле (7):
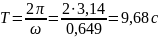
Коэффициент сопротивления при бортовой качке (12):
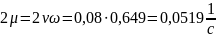
Таким образом уравнение (3) запишется в виде:
|
|
(13) |
Решение этого уравнения является закон свободных колебаний, записанный в виде:
|
|
(14) |
где
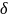 – начальная
фаза колебаний.
– начальная
фаза колебаний.
Найдем решение уравнения (4):
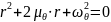 (3)
(3)
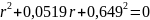
Для решения уравнения (3) найдем дискриминант этого уравнения:
D=0,0027-4
Найдем корни уравнения:
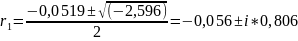
Поскольку полученное решение представляет два комплексно-сопряженных корня, то решение дифференциального уравнения пишется в виде:
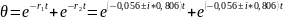
Решение этого уравнения представляет гармоническую функцию:
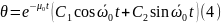
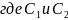 -
произвольные постоянные, определяемые
из граничных условий:
-
произвольные постоянные, определяемые
из граничных условий:
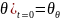
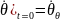
Начальные условия пусть задаются в виде начального отклонения и скорости:
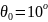
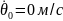
Для
того, чтобы найти произвольные постоянные
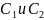 необходимо подставить начальное время
t=0 в выражение (4):
необходимо подставить начальное время
t=0 в выражение (4):
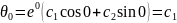 =10
=10
Чтобы найти необходимо продифференцировать выражение (4):
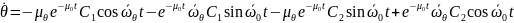
при t=0
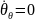
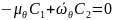
Отсюда
найдем
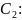
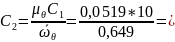 0,80
0,80
Найдем начальную фазу колебаний
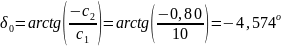
Окончательная форма записи затухающих колебаний:
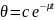 (coswt+
(coswt+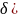 ,
,
где
 ,
с1
и с2
– определяются из начальных условий.
,
с1
и с2
– определяются из начальных условий.
Вычислим точки закона свободных бортовых колебаний для уравнений:
|
|
[1] [2] [3] |
Таблица 1 – Вычисленные точки для построения закона бортовых колебаний судна.
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
t |
0 |
2,42 |
4,84 |
7,26 |
9,68 |
12,09 |
14,51 |
16,93 |
19,35 |
21,77 |
24,19 |
26,61 |
29,03 |
[1] |
10,0 |
9,4 |
8,8 |
8,3 |
7,8 |
7,3 |
6,9 |
6,4 |
6,1 |
5,7 |
5,3 |
5,0 |
4,7 |
[2] |
-10,0 |
-9,4 |
-8,8 |
-8,3 |
-7,8 |
-7,3 |
-6,9 |
-6,4 |
-6,1 |
-5,7 |
-5,3 |
-5,0 |
-4,7 |
[3] |
1,4 |
9,3 |
-1,2 |
-8,2 |
1,0 |
7,2 |
-0,9 |
-6,4 |
0,8 |
5,6 |
-0,7 |
-5,0 |
0,6 |
График закона свободных бортовых колебаний представлен на рисунке 1.
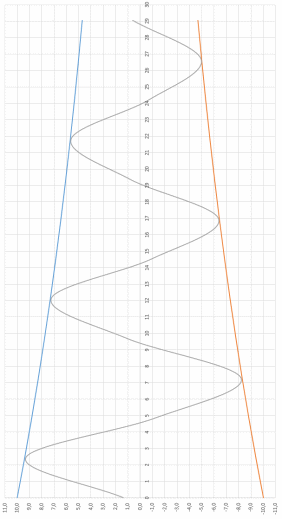
Рисунок 1 – закон свободных бортовых колебаний судна.