
Пример выполнения К-7
.docx(К-7) Сложное движение точки.
Точка
М
движется внутри кольца радиуса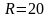 см по закону
см по закону
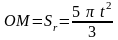 см.
В свою очередь кольцо вращается вокруг
своего диаметра в направлении, указанном
на рис.1, с ускорением
см.
В свою очередь кольцо вращается вокруг
своего диаметра в направлении, указанном
на рис.1, с ускорением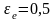 рад/с2.
Найти в момент времени
рад/с2.
Найти в момент времени
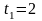 с абсолютную скорость и абсолютное
ускорение точки, если в начальный момент
времени кольцо находилось в покое, а
точка занимала положение
с абсолютную скорость и абсолютное
ускорение точки, если в начальный момент
времени кольцо находилось в покое, а
точка занимала положение
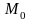 на оси вращения.
на оси вращения.
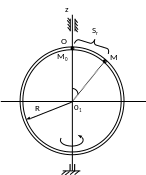
Рис.1
Решение
Сделаем
анализ движения. Относительное движение
точки – движение внутри кольца траектория
– окружность. Переносное движение
сообщается точке вращением кольца
вокруг оси
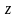 .
.
Найдем положение точки в кольце в заданный момент времени:
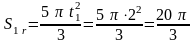 см,тогда
см,тогда 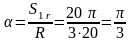 рад или 600.
рад или 600.
Точка
займет положение
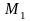 .
.
Абсолютную
скорость найдем по теореме о сложении
скоростей: 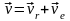 .
.
Алгебраическая
величина относительной скорости: 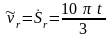 .
.
При
с 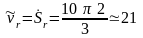 см/с
см/с 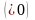 .
.
Вектор
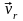 направлен по касательной к окружности
кольца в сторону возрастания
направлен по касательной к окружности
кольца в сторону возрастания
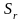 ,
т.к.
,
т.к.
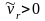 (рис.2).
(рис.2).
Переносную
скорость
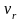 найдем по формуле:
найдем по формуле:
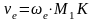 ,
где
,
где
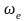 - угловая скорость кольца,
- угловая скорость кольца,
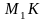 - расстояние от точки
до оси вращения.
- расстояние от точки
до оси вращения.
Т.к.
вращение кольца равнопеременное,
то 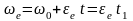 , т.к.
, т.к.
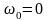 по условию.
по условию.
Тогда
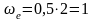 рад/с;
рад/с;
 см.
см.
Тогда 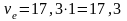 см/с.
см/с.
Вектор
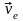 направлен от нас перпендикулярно
плоскости кольца (в сторону вращения
кольца) (рис.2).
направлен от нас перпендикулярно
плоскости кольца (в сторону вращения
кольца) (рис.2).
Т.е.
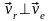 ,
то абсолютная скорость вычисляется по
формуле Пифагора:
,
то абсолютная скорость вычисляется по
формуле Пифагора:
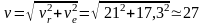 см/с.
см/с.
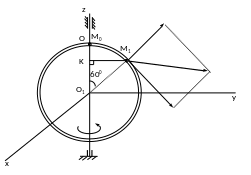
Рис.2
Абсолютное ускорение найдем по теореме о сложении ускорений:
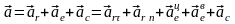 . (1)
. (1)
Находим
относительное касательное ускорение: 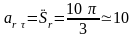 см/с2.
см/с2.
Вектор
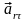 направлен по касательной к кольцу в
сторону возрастания
(рис.3).
направлен по касательной к кольцу в
сторону возрастания
(рис.3).
Находим
относительное нормальное ускорение: 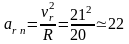 см/с2.
см/с2.
Вектор
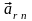 направлен по радиусу к центру кольца
(рис.3).
направлен по радиусу к центру кольца
(рис.3).
Находим переносное центростремительное ускорение:
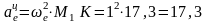 см/с2.
см/с2.
Вектор
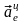 направлен по
направлен по
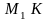 к оси вращения кольца (рис.3).
к оси вращения кольца (рис.3).
Находим переносное вращательное ускорение:
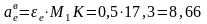 см/с2.
см/с2.
Вектор
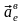 направлен от нас перпендикулярно
плоскости кольца (рис.3).
направлен от нас перпендикулярно
плоскости кольца (рис.3).
Ускорение
Кориолиса находим по формуле: 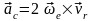 .
.
Тогда
модуль 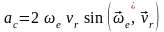 .
.
Угол
между вектором
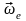 и
и
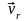 равен 1500.
равен 1500.
Тогда 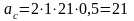 см/с2.
см/с2.
Направление
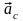 можно найти по правилу Жуковского.
можно найти по правилу Жуковского.
Вектор направлен от нас перпендикулярно плоскости кольца (рис.3).
Проецируем векторное равенство (1) на оси координат:
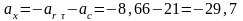 см/с2;
см/с2;
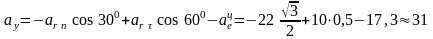 см/с2;
см/с2;
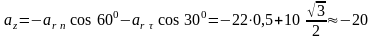 см/с2.
см/с2.
Отсюда 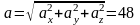 см/с2.
см/с2.
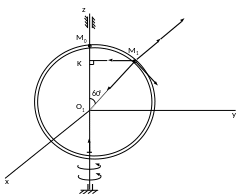
Рис.3
