Работа и мощность тока. Закон Джоуля-Ленца.

Определим работу, совершаемую постоянным током в проводнике, имеющем сопротивление R и находящемся под напряжением 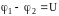. Так как ток пред­ставляет собой перемещение заряда q под действием поля, то работу тока можно оп­ределить по формуле 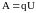. Учитывая формулу и закон Ома, получим:

,

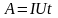С учетом закона Ома для участка цепи 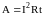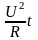₌ , где t - время протекания тока. Поделив обе части равенства на t, получим выраже­ния для мощности постоянного тока Р:

.

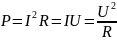Работа тока в системе единиц СИ измеряется в Дж, а мощность - в Вт. На практике применяются также внесистемные единицы работы тока: ватт-час (Втч) и киловатт-час (кВтч). 1Втч - работа тока мощностью 1Вт в течение одного часа. 1Втч=3.610³ Дж.

При прохождении тока по проводнику, проводник нагревается. Нагревание обусловлено тем, что кинетическая энергия движущихся по проводнику электронов (т.е. энергия тока) при каждом их столкновении с ионами металличе­ской решетки переходит в теплоту Q. Если ток идет по неподвижному металличе­скому проводнику, то вся работа тока расходуется на его нагревание и, следуя за­кону сох­ранения энергии, можно записать

Q =

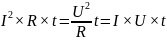
Данные соотношения выражают закон Джоуля-Ленца.

Этот закон был установлен опытным путем Д.Джоулем и независимо от него Э.Ленцем. Применение теплового действия тока в технике началось с открытия в 1873 г. русским инженером А.Ладыгиным лампы накаливания.

На тепловом действии тока основан целый ряд электрических приборов и ус­та­новок: тепловые электроизмерительные приборы, электропечи, электросварочная аппаратура, бытовые электронагревательные приборы - чайники, кипятильники, утюги.

Зависимость сопротивления проводника от температуры:

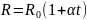, где α – температурный коэффициент сопротивления проводника, t – температура проводника по шкале Цельсия, R₀ - сопротивление при температуре 0⁰С.

Удельная тепловая мощность тока  численно равна количеству теплоты, которая вы­деляется в единице объема за единицу времени. Выделим в проводнике элемен­тарный цилиндрический объем dV с поперечным сечением dS и длиной dl параллель­ной направлению тока, и сопротивлением , 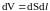. По закону Джоуля-Ленца, за время dt в этом объеме выделится теплота:

.

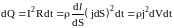Тогда 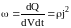и, используя закон Ома для плотности тока 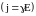и соотно­шение 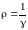, получим:

.

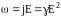Эти соотношения выражают закон Джоуля-Ленца в дифференциальной форме.

Правила Кирхгофа для разветвленных цепей.

До сих пор нами рассматривались простейшие электрические цепи, состоя­щие из одного замкнутого неразветвленного контура. Расчет I, R,  в такой цепи выполняется с помощью законов Ома.

Более сложной является разветвленная электрическая цепь, состоящая из нескольких замкнутых кон­ту­ров, имеющих общие участки. В каждом контуре мо­жет быть несколько источников тока. Силы тока на от­дельных участках замкнутого контура могут быть раз­личными по величине и направлению. В 1847 г. Г.Кирхгоф сформулировал два правила, значительно упрощающих расчет разветвленных цепей.

Первое правило Кирхгофа: алгебраическая сумма сил токов в узле равна нулю:

.

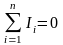Узел – это точка цепи, в которой сходятся не менее трех про­водников. Ток, входящий в узел, считается положительным, выходящий - отрицательным.

Второе правило Кирхгофа относится к любому замкнутому контуру, выде­ленному в разветвленной цепи: алгебраическая сумма произведений токов на со­противления, включая и внутренние, на всех участках замкнутого контура равна алгебраической сумме электродвижущих сил, встречающихся в этом контуре: .

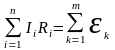Контур ‑ это замкнутый участок цепи, по которому можно пройти и вернуться в исходную точку. Первое и второе правила Кирхгофа по­зволяют составить систему линейных алгебраичес­ких уравнений, которые связывают пара­метры (I, R, 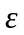) и позволяют, зная одни, найти другие.

10.1. Ток I в проводнике меняется со временем t по уравнению I=4+2t, где I – в Амперах и t- в секундах. Какое количество электричества q проходит через поперечное сечение проводника за время от t₁=2c до t₂=6с? При каком постоянном токе I₀ через поперечное сечение проводника за то же время проходит такое же количество электричества?

Дано: I= 4 + 2t(A), t₁=2c, t₂ =6c.

Найти q, I₀.

По определению: 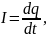отсюда:

q=

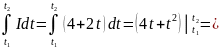
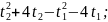
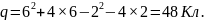
Постоянный ток определяется по формуле:

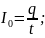
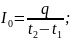
Ответ:

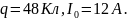
10.4. Обмотка катушки из медной проволоки при t₁=14⁰C имеет сопротивление R₁=10 Ом. После пропускания тока сопротивление обмотки стало равным R₂=12,2 Ом. До какой температуры t₂ нагрелась обмотка? Температурный коэффициент сопротивления меди α=4,15*10^-3К^-1.

Дано: t₁= 14⁰C, R₁ =10 Ом, R₂ = 12,2 Ом, α=4,15*10^-3К^-1

Найти: t₂.

Согласно формуле зависимости сопротивления проводника от температуры:

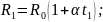
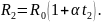
Поделим верхнее соотношение на нижнее:

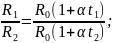
отсюда:

;

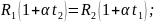
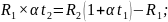
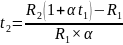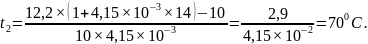
Ответ: t₂ = 70⁰С.

10.12. Два последовательно соединенных элемента с одинаковыми Э.Д.С. ε₁ =ε₂=2В и внутренними сопротивлениями r₁=r1 Ом, r₂=1,5 Ом замкнуты на внешнее сопротивление R=0,5 Ом.

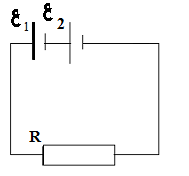
Рис. 5

Найти разность потенциалов U на зажимах каждого элемента.

Дано: ε₁ =ε₂=2В, r₁=1 Ом, r₂=1,5 Ом, R=0,5 Ом.

Найти U₁ и U .

Разность потенциалов на неоднородном участке цепи определяется по формуле:

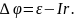
По закону Ома для замкнутой цепи:

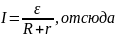
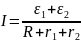
Следовательно, разность потенциалов на зажимах первой Э.Д.С.:

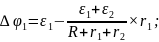
Соответственно на зажимах второй Э.Д.С.:

.

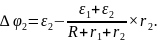
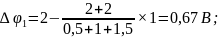
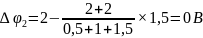Ответ: 0,67В, 0В.

Электромагнетизм

Магнитное поле создается только движущимися зарядами или движущимися заряженными телами, а также постоянными магнитами. Этим магнитное поле отличается от электрического поля, которое создается как движущимися, так и неподвижными зарядами и действует как на одни, так и на другие.

Основной характеристикой магнитного поля является вектор магнитной индукции 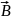. За направление магнитной индукции в данной точке поля принимают направление северного полюса бесконечно малой магнитной стрелки. Графически магнитные поля изображаются силовыми линиями магнитной индукции, то есть кривыми, касательные к которым в каждой точке совпадают с направлением вектора В.

Направление вектора индукции магнитного поля проводников с током определяется по правилу правого винта или буравчика. Большой палец правой руки ориентируют в направлении тока, тогда остальные пальцы в согнутом положении указывают направление силовых линий магнитного поля. Линии вектора магнитной индукции всегда замкнуты и охватывают проводник с током. Этим они отличаются от линий напряженности электрического поля, которые начинаются на положительных и кончаются на отрицательных зарядах, т.е разомкнуты. Линии магнитной индукции постоянного магнита выходят из одного полюса, называемого северным (N) и входят в другой - южный (S). Если разрезать магнит, картина сохраняется, получаются более мелкие магниты со своими северными и южными полюсами, т.е. полюса разделить невозможно, потому что свободных магнитных зарядов, в отличие от электрических зарядов, в природе не существует. Было установлено, что внутри магнитов имеется магнитное поле и линии магнитной индукции этого поля являются продолжением линий магнитной индукции вне магнита, т.е. замыкают их. Подобно постоянному магниту магнитное поле соленоида – катушки из тонкой изолированной проволоки с длиной намного больше диаметра, по которой течет ток. Магнитная индукция в системе СИ измеряется в Н/(А∙м), этой величине присвоено специальное наименование – [Tл].

Магнитные поля, существующие в природе, разнообразны по масштабам и по вызываемым эффектам. У Земли есть свое магнитное поле. В околоземном пространстве магнитное поле образует магнитную ловушку для заряженных частиц высоких энергий. Происхождение магнитного поля Земли связывают с движениями проводящего жидкого вещества в земном ядре. Магнитное поле Солнца играет важнейшую роль во всех происходящих на Солнце процессах – вспышках, появлении пятен и протуберанцев, рождении солнечных космических лучей.

Закон Био-Савара-Лапласа:

,

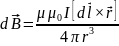где 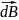-вектор индукции магнитного поля, созданного элементом тока 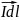на расстоянии радиус-вектора 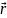от него, 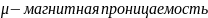среды, μ₀ –магнитная постоянная, μ₀=4π*10^-7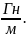

Вектор индукции магнитного поля, созданного проводником в целом:

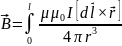
Введем понятие напряженности магнитного поля Н, она связана с индукцией магнитного поля соотношением: .

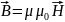Для полей, обладающих некоторой симметрией, получены формулы расчета напряженности.

Напряженность магнитного поля в центре кругового витка:

,

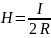где I - сила тока, R - радиус кругового витка.

Напряженность магнитного поля на оси кругового витка:

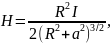
где I - сила тока, R - радиус кругового витка, а – расстояние от точки на оси, восстановленной из центра витка, где определяется напряженность магнитного поля, до центра витка.

Напряженность магнитного поля, созданного бесконечно длинным проводником:

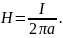
где I - сила тока, а – кратчайшее расстояние от точки до проводника.

Напряженность магнитного поля внутри тороида или бесконечно длинного соленоида:

Н=nI,

где n –число витков, приходящихся на единицу длины бесконечно длинного соленоида, а I – сила тока, текущего по соленоиду.

Ампер установил, что сила, с которой магнитное поле действует на элементарный проводник с током I и длиной dl:

,

_где 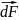- сила, действующая на элемент тока , находящийся в магнитном поле c индукцией .

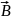Вектор dl совпадает по направлению с током. Данная формула выражает закон Ампера: сила, действующая на элемент проводника с током в магнитном поле, равна произведению силы тока на векторное произведение элемента длины проводника и магнитной индукции поля.

Направление может быть найдено по правилу левой руки: если ладонь левой руки расположить так, чтобы вектор был направлен в ладонь, а четыре вытянутых пальца указывали направление тока в проводнике, то отставленный под прямым углом большой палец укажет направление силы, действующей на элемент проводника с током.

Чтобы найти силу, действующую со стороны магнитного поля на проводник конечной длины в магнитном поле, необходимо определить геометрическую сумму сил, действующих на все малые элементы данного проводника, т.е.

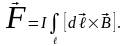
Законы Био – Савара – Лапласа и Ампера применяются для определения силы взаимодействия двух параллельных проводников с током. Каждый из проводников создает магнитное поле, которое действует на другой проводник. Направление определяется правилом правого винта, а его модуль по закону Био – Савара – Лапласа. Тогда, согласно закону Ампера, dF=IB1dl или

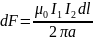
Е сли токи текут в противоположных направлениях, то возникающие между ними силы отталкивают проводники друг от друга, а параллельные токи (одного направления) притягиваются.

Сила, действующая со стороны магнитного поля на движущиеся заряды, называется силой Лоренца:

,

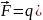где q – величина заряда, движущегося со скоростью v в магнитном поле с индукцией B.