
9060_d71504bbdcb8f95ffb66490c84b51bf8
.pdf
Например,
æCO2 |
|
ö |
|
æ0 2 1öæHö |
||||||
çH O |
|
÷ |
= |
ç |
2 |
1 |
0 |
֍O |
÷. |
|
ç |
2 |
|
÷ |
|
ç |
|
|
|
֍ |
÷ |
çH CO |
÷ |
|
ç |
2 |
3 |
1 |
֍C |
÷ |
||
è |
2 |
3 |
ø |
|
è |
|
|
|
øè |
ø |
Учитывая, что a А = 0, получаем, что bВ = 0. Поскольку В — единичная матрица, то отсюда следует, что ab = 0. Атомная матрица b известна, стехиометрическая матрица a является искомой.
2.10.3. Статические модели экономики
Рассмотрим задачи балансового анализа. Цель балансового анализа — ответить на вопрос, возникающий в макроэкономике: каким должен быть объем производства каждой из n отраслей, чтобы удовлетворить все потребности в продукции этой отрасли, при- чем каждая отрасль выступает как производитель некоторой продукции, а с другой стороны, как потребитель и своей, и чу- жой продукции. Математическая модель такой задачи разработана в 1934 г. Леонтьевым.
Пусть xi — общий (валовой) объем продукции i-й отрасли (i = 1,n), xj — объем продукции i-й отрасли, потребляемый j-й отраслью в процессе производства ( j = 1,n), yi — объем конечного продукта i-й отрасли для непроизводственного потребления.
Так как валовой объем продукции любой i-й отрасли равен суммарному объему продукции, потребляемой n отраслями, и конечного продукта, то
n
xi = å xij + yi (i = 1,n).
j =1
Эти уравнения называют соотношениями баланса. Рассмотрим стоимостный межотраслевой баланс и введем ко-
эффициенты прямых затрат aij = xij , (i, j = 1,n), покрывающие за- xj
траты продукции i-й отрасли на производство единицы продукции j-й отрасли.
При предположении aij = const соотношения баланса примут
âèä
n
xi = åaij xj + yi (i = 1,n).
j =1
#
|
|
æ x1 |
ö |
|
|
|
ç |
÷ |
|
В матричном виде X = AY + Y, где X = ç x2 |
÷ |
— вектор валового |
||
|
|
ç |
÷ |
|
|
|
L |
÷ |
|
æ y |
ö |
ç |
|
|
ç |
÷ |
|
||
ç 1 |
÷ |
è xn |
ø |
|
выпуска, Y = ç y2 |
÷ |
— вектор конечного продукта, А = (аij), |
||
çL |
÷ |
|
|
|
ç |
÷ |
|
|
|
ç |
÷ |
|
|
|
è yn |
ø |
|
|
|
i, j = 1,n, — матрица прямых затрат.
Основная задача межотраслевого баланса состоит в отыскании такого вектора валового выпуска Х, который при известной матрице прямых затрат А обеспечивает заданный вектор конечного продукта Y.
Литература: [7. С. 9–35; 189–230]; [9. С. 42, 72–130]; [16. С. 222– 241; 259–275].
3.АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
ÈВ ПРОСТРАНСТВЕ: ПРЯМАЯ И ПЛОСКОСТЬ
Опорный конспект ¹ 3
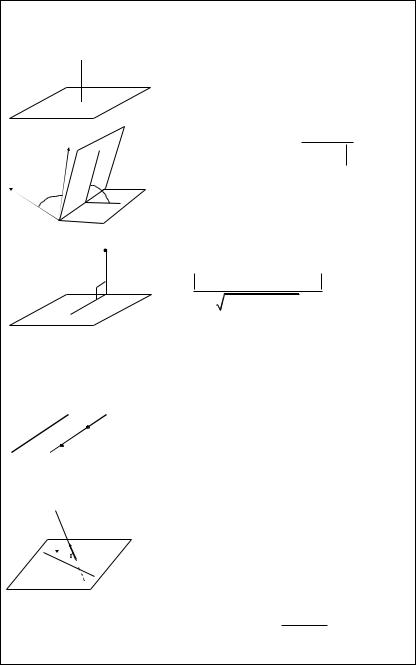
3.1. Прямая на плоскости
k = tgj, b Û y = kx + b, M0(x0, y0)Î L Þ
Y |
|
|
Þ y - y0 = k(x - x0 ) |
|
|
|
|
|
|||||
|
|
L |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||||
|
M |
|
· |
|
|
|
k2 |
- k1 |
|
|
|
||
|
|
0 |
q = (L1, L2), tg q = |
|
|
|
, |
|
|
||||
b |
j |
|
|
|
|
|
1 + k2k1 |
|
|
|
|||
|
|
|
L1 P L2 Û k2 = k1, L1 ^ L2 Û k1k2 = -1 |
||||||||||
O |
|
X |
Ax + By + C = 0 — общее уравнение L |
||||||||||
|
|
|
|||||||||||
Y |
|
|
(A2 + B 2 ¹ 0), Ì (x , y ), M (x , y ) Î L Þ |
||||||||||
|
|
1 |
1 |
|
1 |
|
2 |
2 |
2 |
||||
|
K (xK, yK) L |
Þ |
y - y1 |
= |
x - x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
d |
|
|
y2 - y1 x2 - x1 |
|
|
|
|
|
|
|
||
d = AxK + ByK +C
A2 + B2
OX
#
3.2. Плоскость в пространстве
r
 N
N
W  M
M
M0
|
r |
W2 |
|
N1 |
|
|
|
|
r |
|
|
N2 |
|
Q |
|
|
W1
K
d
W
M |
(x , y , z ) Î W, Ì(x, y, z) Î W, |
|
r0 |
0 0 0 |
uuuuuuur r |
N= {A, B,C}, M0M ^ N Û
ÛA(x - x0) + B(y - y0) +C(z - z0) = 0,
Ax + By + Cz + D = 0 — общее уравнение W |
||||||
r r |
|
r |
|
|
r |
|
|
N |
|
× N |
|||
· |
|
|
||||
cosQ = cos(N1, N2) = |
|
r 1 |
|
|
|
r 2 |
|
|
|
||||
|
|
N1 |
|
|
|
N2 |
|
|
|
r |
r |
|
|
|
|
|
|
|
|
|
W1 ^ W2 Û N1 × N2 = 0 Û |
|
|
|
|
|
|
|||||||
Û A1A2 + B1B2 + C1C2 = 0 |
|
|
|
|
|
|
|||||||
|
|
|
r |
r |
|
|
|
A |
|
B |
|
C |
|
W |
P W |
2 |
Û N |
´ N |
2 |
= 0 Û |
|
1 |
= |
1 |
= |
|
1 |
|
|
|
|
|
|||||||||
1 |
|
1 |
|
|
|
A2 |
|
B2 |
|
C2 |
|||
|
|
|
|
|
|
|
|
|
|
||||
d = AxK + ByK +CzK + D A2 + B2 +C2
3.3Прямая в пространстве. Взаимное расположение прямой
èплоскости
r
r  M
M  S = {m, n, p} P L, M0 (x0, y0, z0}Î L,
S = {m, n, p} P L, M0 (x0, y0, z0}Î L,
S
|
M0 |
|
|
uuuuuuur |
r |
Û |
|
x - x |
|
= |
y - y |
= |
|
z - z |
0 |
||||||||||||
|
|
|
|
|
M |
0 |
M P S |
|
|
0 |
|
|
|
0 |
|
|
|
||||||||||
L |
|
|
|
|
|
|
m |
|
|
n |
|
|
p |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
M1(x1,y1,z1}, M2(x2,y2,z2}Î L Þ |
|
|||||||||||||||||||||
L2 |
|
|
|
|
|
|
r |
uuuuuuuur |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Þ S = M1M2 Þ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
r |
r |
|
Þ |
|
|
x - x |
= |
|
y |
- y |
|
|
= |
z - z |
|
|
|
|
|
|
||||||
S |
Q S |
|
W |
|
|
|
1 |
|
|
1 |
|
|
|
|
1 |
. |
|
|
|
||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
|
|
|
x2 - x1 |
|
y2 |
- y1 |
|
|
z2 - z1 |
|
|
|
|
|
|
|||||||||
L |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L1 Î W, L2 Ï W, S1 P L1 Þ |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
r |
r |
|
|
|
|
r |
r |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S × S |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
· |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
cos Q = cos(S |
, S |
)= |
|
r1 |
|
r |
2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
S1 |
|
S2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
#!

r
N
L
r
S  Q
Q 
W 
|
r |
W2 |
|
r |
N1 |
||
2 Q |
r |
||
N |
|||
S |
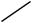 L W1
L W1
|
|
|
|
|
|
|
|
r |
|
|
|
r |
|
|
|
r |
r |
|
|
|
|
N |
|
× S |
|
||
|
|
|
|
||||||||||
sin Q = |
|
· |
|
|
= |
|
|
|
|
|
|
|
|
cos(N |
,S) |
|
|
|
r |
|
|
|
r |
|
|||
|
|
|
|
|
|
||||||||
|
r |
r |
|
|
|
|
|
N |
|
|
|
S |
|
|
= 0, |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
L P W Û N |
× S |
|
|
|
|
|
|
|
|
||||
|
r |
|
r |
|
|
|
|
|
|
|
|
||
L ^ W Û N ´ S = 0 |
|
|
|
|
|
||||||||
r |
r |
r |
|
|
S = N1 |
´N2 |
|
|
|
ì A1x + B1y +C1z + D1 = 0, |
|
|||
L: íA x + B y +C |
z + D = 0 |
— общие |
||
î |
2 |
2 2 |
2 |
|
уравнения L
3.1.Прямая на плоскости
3.1.1.Уравнение линии на плоскости
Пусть на плоскости выбрана прямоугольная система координат.
О: Уравнение F (x, y) = 0 называется уравнением линии на плоскости, если ему удовлетворяют координаты (x, y) каждой точки данной линии и не удовлетворяют координаты точек, не лежащих на ней.
Часто линия на плоскости задается характерными геометрическими свойствами, по которым находится ее уравнение. Координаты произвольной точки линии являются текущими координатами этой точки.
В качестве примера рассмотрим вывод уравнения окружности.
О: Окружностью называется геометрическое место точек, равноудаленных от данной т. С (x0, y0) — центра окружности.
Пусть М (x, y) — точка с текущими координатами, лежащая на окружности, R — расстояние от т. М до центра С, тогда
#"

ÑÌ
 = R Û (x - x0 )2 + (y - y0 )2 = R.
= R Û (x - x0 )2 + (y - y0 )2 = R.
Нормальное уравнение окружности получаем, возводя обе ча- сти равенства в квадрат: (x - x0)2 + (y - y0)2 = R2.
Уравнение прямой на плоскости получим в различных формах в зависимости от исходных данных.
3.1.2. Уравнение прямой с угловым коэффициентом
Рассмотрим на плоскости XOY произвольную прямую L, не параллельную OY. Ее положение вполне определяется углом j = (OX·, L) между прямой L и осью OX и отрезком b, отсекаемым прямой L на оси OY. Отметим, что под углом j понимается наименьший неотрицательный, т.е. отсчитываемый против хода ча- совой стрелки от OX к L, угол. Составим уравнение этой прямой. Обозначим через М (x, y) точку с текущими координатами на прямой L (рис. 3.1), B (0, b), тогда
uuuur |
= {x, y, - b}, tg j = |
y - b |
, |
|
BM |
||||
|
||||
|
|
x |
||
т.е. y = x tg j + b. Обозначив k = tg j, получим уравнение y = kx + b, называемое уравнением прямой с угловым коэффициентом k.
Y 
L
M (x, y)
ü
 ï
ï
 ýï y - b
ýï y - b
Bj }b









 þ
þ
O |
x |
X |
Ðèñ. 3.1
3.1.3. Уравнение прямой, проходящей через заданную точку (уравнение пучка прямых)
Положение прямой L, не параллельной оси OY, на плоскости вполне определяется заданием угла j = (OX·, L) è ò. Ì0(x0, y0) О L. Составим уравнение этой прямой. Подставим координаты т. М0 в уравнение прямой L с угловым коэффициентом, где слагаемое b пока не известно. Получим y0= kx0+ b. Вычтем теперь данное ра-
##
венство из уравнения y = kx + b. Получим так называемое уравнение прямой, проходящей через заданную точку М0: y - y0 = k (x - x0).
Если угловой коэффициент k не задан, то уравнение определит пучок прямых, проходящих через т. М0.
Часто употребляемые при решении задач общее уравнение прямой и уравнение прямой, проходящей через две заданные точки, будут выведены далее как частные случаи общего уравнения плоскости и уравнений прямой в пространстве соответственно.
3.1.4. Угол между двумя прямыми на плоскости. Условия параллельности и перпендикулярности
О: Углом q между двумя прямыми L1 è L2 на плоскости будем называть наименьший угол, на который нужно повернуть прямую L1 в положительном направлении так, чтобы она совпала с прямой L2.
Пусть прямые L1 è L2 заданы уравнениями:
L1: y = k1x + b1, k1 = tg j1, L2: y = k2x + b2, k2 = tg j2. Из рис. 3.2 видно, что j2 = j1+ q,
Y |
L2 |
|
|
|
L1 |
|
|
|
|
|
|
|
|
q |
|||
|
|
|
|
|
|
j |
j2 |
||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
O |
X |
||||
|
|
|
|
|
|
Ðèñ. 3.3 |
|
|
|
||
tg q = tg(j |
2 |
- j ) = |
|
|
|
tg j2 - tg j1 |
. |
Окончательно tg q = |
k2 - k1 |
. |
|
|
|
|
|
|
|||||||
|
1 |
1 |
+ tg j1 × tg j2 |
|
1 + k1k2 |
||||||
|
|
|
|
||||||||
Прямые L1 è L2 параллельны в том и только том случае, когда tg j1 = tg j2, ò.å. L1 || L2 Û k1= k2. В случае перпендикулярности прямых tg q не существует, т.е. L1 ^ L2 Û k1k2 = -1.
#$
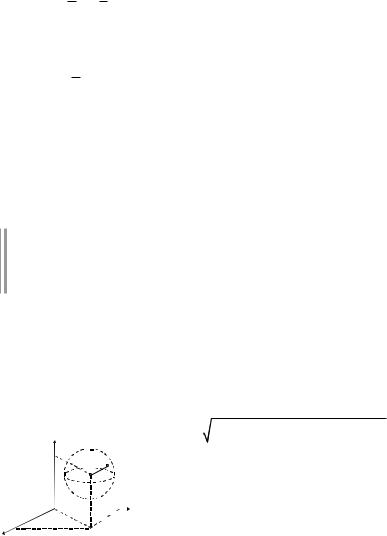
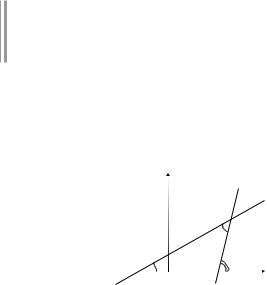
Задача. Найти уравнение прямой L, проходящей через т. М0(-1, 2) и перпендикулярной к прямой L1: 3x - 4y + 5 = 0.
 Запишем уравнение пучка прямых, проходящих через т.М0: y - 2 = k(x + 1). Угловой коэффициент k находим из условия перпендикулярности L ^ L1. Так как уравнение L1 можно переписать
Запишем уравнение пучка прямых, проходящих через т.М0: y - 2 = k(x + 1). Угловой коэффициент k находим из условия перпендикулярности L ^ L1. Так как уравнение L1 можно переписать
â âèäå y = 43 x + 45 , то ее угловой коэффициент k1=3/4. Теперь ис-
пользуем формулу k1k = -1, тогда k = - 4/3. Подставим найденный угловой коэффициент в уравнение пучка:
y - 2 = - 43 (x +1) èëè 4x + 3y - 2 = 0 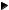
3.2.Плоскость в пространстве
3.2.1.Уравнение поверхности
Пусть в пространстве выбрана прямоугольная система координат XYZ.
О: Уравнение F (x, y, z) = 0 называется уравнением поверхности, если ему удовлетворяют координаты (x, y, z) каждой точки данной поверхности и не удовлетворяют координаты точек, не лежащих на ней.
Аналогично линиям на плоскости, поверхности могут быть заданы характерными геометрическими свойствами, по которым находятся их уравнения. Так, сферой называется гмт, равноудаленных от заданной т. С (x0, y0, z0) — центра сферы. Обозначим через M (x, y, z) точку с текущими координатами на сфере, R — расстояние от т. М до центра С. Тогда (рис. 3.3)
ZÑÌ
 = R Û x - x0 2 + y - y0 2 + z - z0 2 = R.
= R Û x - x0 2 + y - y0 2 + z - z0 2 = R.
z0 |
M |
Нормальное уравнение сферы полу- |
|||||
|
|
|
|
C |
|||
|
|
|
|
||||
|
|
|
|
чим, возведя обе части равенства в квад- |
|||
|
|
|
|
|
|||
|
|
|
|
y0 |
ðàò: |
|
|
X |
|
|
Y |
+ (y - y )2 |
+ (z - z )2 = R2. |
||
|
|
(x - x )2 |
|||||
x |
|
|
|||||
|
|
0 |
0 |
0 |
|||
0
X
Ðèñ. 3.3
#%
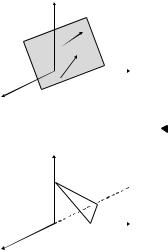
3.2.2. Уравнение плоскости, проходящей через заданную точку (уравнение связки плоскостей)
Положение плоскости W в пространстве вполне определяется r
заданием вектора N = {A, B,C}, перпендикулярного к плоскости
(нормальный вектор), и т. М0(x0, y0, z0). Найдем уравнение этой |
||
плоскости. Пусть т. М(x, y, z) О W — точка с текущими координа- |
||
uuuuuuur |
r uuuuuuur |
r |
тами. Тогда M0M |
^ N Û M0M |
× N = 0 (рис. 3.4). Записав условия |
перпендикулярности через координаты, получим уравнение плоскости, проходящей через заданную точку:
Z |
|
|
|
A(x - x0) + B(y - y0) + C(z - z0) = 0. |
|||
|
|
|
|
|
r |
||
|
|
|
|
|
|
|
|
|
|
r |
|
|
Если координаты вектора N заранее |
||
|
|
|
|
не заданы, то мы имеем уравнение связ- |
|||
|
|
N |
|
|
|||
W |
M |
|
ки плоскостей. |
|
|||
|
|
|
|
|
|
||
|
|
|
|
Y |
Задача. Найти уравнение плоскости, |
||
O |
M0 |
|
|||||
|
|
|
|
проходящей через т. М (-1, 2, 3) перпен- |
|||
|
|
|
|
|
|||
X |
|
|
|
|
|
uuuuuur0 |
|
|
|
|
дикулярно вектору M0K, ãäå K(0, -1, 2). |
||||
Ðèñ. 3.4 |
|
|
|||||
|
|
|
|
|
Уравнение связки плоскостей, прохо- |
||
Z |
|
|
|
дящих через т. М0: A(x + 1) + B (y - 2) + |
|||
|
|
|
|
|
+ C(z - |
3) = 0. |
Нормальный вектор |
|
|
|
|
|
r uuuuuur |
|
|
10 M3 |
|
|
N = M0K |
= {1, - 3, |
-1}. Таким образом, |
||
|
|
|
M1 |
|
1(x + 1) - 3(y - 2) - 1(z - 3) = 0 èëè x - 3y - |
||
|
|
|
-10 |
|
- z + 10 = 0 есть искомое уравнение плос- |
||
|
|
|
M2 |
|
|||
O |
|
10/3 |
Y |
кости. Чтобы построить эту плоскость, |
|||
|
|
|
|
строим три точки плоскости, лежащие на |
|||
|
|
|
|
|
|||
X |
|
|
|
осях координат (рис. 3.5): М1(-10,0,0), |
|||
Ðèñ. 3.5 |
|
|
|||||
Ì2(0,10/3,0), Ì3(0,0,10), затем их последовательно соединяем отрезками прямых,
лежащих в координатных плоскостях 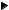
3.2.3. Общее уравнение плоскости, его частные случаи
Из п. 3.1.2 следует, что плоскость определяется уравнением I степени относительно текущих координат. Справедливо и обратное.
Т: Всякое невырожденное уравнение I степени относительно текущих координат
#&

Ax + By + Cz + D = 0 (A2 + B 2 + C 2 ¹ 0) |
(3.1) |
определяет плоскость в пространстве и называется общим уравнением плоскости n
q Возьмем т. М0(x0, y0, z0), координаты которой удовлетворяют данному уравнению. Тогда
Ax0 + By0 + Cz0+ D = 0. |
(3.2) |
Вычитая из уравнения (3.1) равенство (3.2), получаем уравнение плоскости, проходящей через заданную точку: A(x - x0) + + B(y - y0) + C(z - z0) = 0. На плоскости XOY (z = 0) уравнение (3.1) дает общее уравнение прямой Ax + By + D = 0 (A2 + B2 ¹ 0) x
Рассмотрим частные случаи общего уравнения плоскости: a) D = 0 Ю W: Ax + By +Cz = 0 Ю т.O (0, 0, 0)О W;
á) A = 0 Þ W: By +Cz + D = 0 Þ W POX ; â) A = B = 0 Þ W: Cz + D = 0 Þ W P XOY ; ã) A = D = 0 Þ W: By +Cz = 0 ÞOX Ì W.
В евклидовом пространстве Rn с ортонормированным базисом вводится понятие гиперплоскости.
Ее общее уравнение
A1x1 + A2x2 + ... + Anxn + B = 0, Ài,B ÎR, i = 1,n,
r
N = {A1, A2, ..., An} — нормальный вектор гиперплоскости.
3.2.4. Угол между плоскостями.
Условия параллельности и перпендикулярности
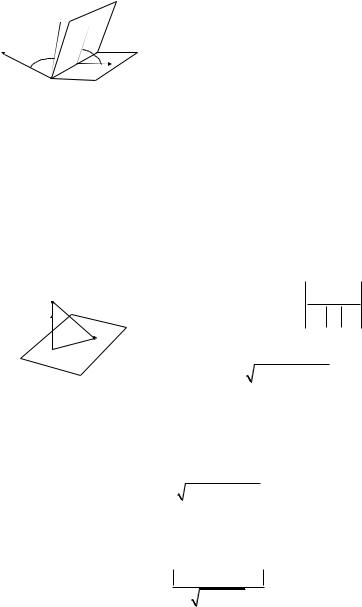
О: Углом Q между двумя плоскостями называется один из двух смежных двугранных углов между этими плоскостями.
Пусть заданы нормальные векторы |
|||||||||||
r |
|
|
r |
|
|
|
|
|
|
||
N1 |
= {A1, B1,C1} è N2 = {A2, B2,C2} |
||||||||||
плоскостей W1 |
è W2 |
соответственно, тогда (рис. 3.6 ) |
|||||||||
|
|
|
|
|
r |
|
|
|
r |
||
|
|
|
cosQ = |
|
N |
× N |
|||||
|
|
|
|
r1 |
|
|
|
r 2 |
|
. |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
N1 |
|
|
|
N2 |
|
|
#'
r
N1 W2
W2
r |
Q |
|
|
N2 Q |
|
|
W1 |
Условия параллельности и перпендикулярности плоскостей получим, рассматривая расположение их нормальных векто-
ðîâ: |
r r |
r |
r |
|
|
|
|||
|
W1 P W2 Û N1 P N2 |
Û N1 |
´ N2 |
= 0 Û |
Ðèñ. 3.6 |
|
|
|
|
A1 |
|
B1 |
|
C1 |
|
|
|
|
|
Û |
= |
= |
; |
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
A2 |
|
B2 |
C2 |
|
|
r |
r |
r |
r |
|
|
|
|
|
|
|
W1 ^ W2 Û N1 |
^ N2 |
Û N1 |
× N2 |
= 0 Û A1A2 + B1B2 |
+C1C2 = 0. |
|||||
3.2.5. Расстояние от точки до плоскости
Найдем расстояние d от т. K (xK, yK, zK)П W до плоскости W. Пусть известны т. M0r(x0, y0, z0) О W и нормальный вектор N = {A, B,C} плоскости W. Тогда (рис 3.7)
|
uuuuur |
|
uuuuuur |
|
uuuuuur |
r |
|
|
K |
|
|
M |
K |
× N |
|
||
|
d = K ¢K |
= |
ïðNr M0K |
= |
|
0 r |
|
= |
r |
d |
|
|
|
|
N |
|
|
NW
|
K ¢ |
M0 |
= |
|
A(xK - x0) + B(yK - y0) +C(zK - z0) |
|
. |
|||
|
|
|
||||||||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
A2 + B2 +C2 |
||||
|
Ðèñ. 3.7 |
|
|
|
|
|
|
|
|
|
Если дано общее уравнение W: |
|
|
|
|
||||||
|
|
Ax + By + Cz + D = 0, |
|
|
|
|
||||
òî |
|
d = |
|
AxK + ByK +CzK + D |
|
. |
|
|
||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
A2 + B2 +C2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
В частности, на плоскости XOY получаем формулу для вычисления расстояния d от т. K (xK, yK) до прямой L: Ax + By + C = 0,
d = AxK + ByK +C .
A2 + B2
Задача. Найти расстояние между параллельными плоскостями W1: x - 2y + 3z + 2 = 0 è W2: 2x - 4y + 6z - 9 = 0.
$
