Лекция 14. Стационарное уравнение Шредингера. Частные случаи,

Решение уравнения Шредингера является очень сложной задачей и не всегда достижимой, однако часто практическое значение имеет не само решение, а оценка физических величин, при которых оно существует.

Если силовое поле, в котором движется частица, постоянно во времени, то силовая функция U не зависит от времени, и тогда можно разделить переменные координат и времени, т.е. волновую функцию можно представить в виде:

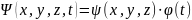(12.5)

Подставим это выражение в уравнение Шредингера:

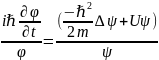, или, после математических преобразований: (12.6)

Слева от знака равенства функция только времени, а справа – только координат. Это возможно, если левая и правая стороны равны некоторой постоянной, назовем ее Е, и запишем соотношение (12.6) еще раз:

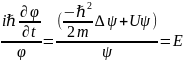(12.7)

Уравнение (12.7) распадается на 2:

1. Первое уравнение . (12.8)

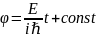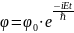Решением этого уравнения является функция: ln ; или, . (12.9)

Из вида решения для временной части волновой функции следует, что уравнение Шредингера находится в согласии с предположением о связи полной энергии частицы Е с частотой волн де Бройля.

2. Второе уравнение 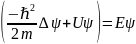, или, после преобразований:

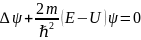. (12.10)

Данное уравнение получило название стационарного уравнения Шредингера.

Стационарное – это уравнение Шредингера для так называемых стационарных состояний, находясь в которых частица имеет определенные, не меняющиеся со временем характеристики.

Последнее уравнение имеет решение не при всех значениях Е. Значения Е_n, при которых решение существует, называются собственными значениями оператора энергии или оператора Гамильтона 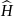. Пси-функции ψ_n , которые являются решением стационарного уравнения при данных значениях Е_n, называются собственными функциями оператора Гамильтона. Если обозначить эту функцию через ψ_n(x), то окончательное решение запишется в виде:

(12.11)

Таким образом, состояние частицы в данный момент времени описывается периодической функцией времени с циклической частотой ω_n= , определяемой значением полной энергии Е_n . Эта связь энергии частицы Е с частотой волны де Бройля является важнейшей основой квантовой механики.

Вероятность нахождения частицы в какой-то точке пространства пропорциональна квадрату модуля функции:

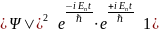
Видно, что вероятность нахождения частицы в какой-то области пространства, перестает зависеть от времени, поэтому подобные состояния, с определенными Е_n , называют стационарными.

Частные случаи.

1. Движение свободной частицы.

При свободном движении частицы ее полная энергия совпадает с кинетической, а скорость постоянна. Направим ось х вдоль вектора скорости v. Тогда стационарное уравнение Шредингера можно записать в следующем виде:

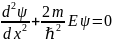. (12.12)

Решением этого уравнения будет гармоническая функция:

,

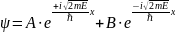где = к - волновое число.

Полное решение общего уравнения Шредингера

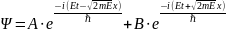(12.13)

Это выражение соответствует суперпозиции двух плоских волн одинаковой частоты, распространяющихся в противоположных направлениях. Сравнивая полученное выражение с общим выражением плоской монохроматической волны, можно показать, что волновое число к для свободной частицы равно:

k = , а частота - ω= .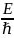

2. Электрон в одномерном потенциальном ящике. Квантование энергии частицы.

Рассмотрим электрон, движущийся в потенциальном поле, изображенном на рис. 12.1. Потенциальная энергия электрона вне и внутри потенциального «ящика» описывается следующими соотношениями:

U =  в областях 1, 3 для 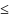x 0 и x 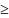  a; U = 0 в области 2 для 0  x a. (12.14)

В классической электронной теории считалось, что вне металла потенциальная энергия электрона равна нулю, а внутри металла она отрицательна и численно равна работе выхода электрона из металла.

Рис. 12.1

Иными словами, считалось, что движение электрона ограничено потенциальным барьером прямоугольной формы с плоским дном. Рассматриваемый нами потенциальный «ящик» с бесконечно высокими стенками более прост, чем реальный случай электрона в металле. Применим к электрону, движущемуся в таком потенциальном поле, уравнение Шредингера в форме (12.10) и учтем, что для одномерной задачи значок .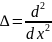

Уравнение Шредингера для электрона в потенциальном поле нашего случая будет иметь вид:

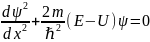. (12.15)

Это уравнение может иметь решение, удовлетворяющие условиям (12.14) только в том случае, если волновая функция 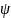(х) будет обращаться в нуль на стенках «ящика»: (0) = (а)=0 , (12.16) так как в области 0  x a имеем U=0, а для областей 1, 3 - U= . Таким образом, для электрона в потенциальном «ящике» с бесконечно высокими стенками решение уравнения Шредингера должно быть таким, чтобы:

= 0, |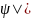 ² =0 вне области 0  x a.

То есть вероятность найти электрон вне «ящика» равна нулю.

С учетом того, что вне «ящика» электрон находиться не может, задача о движении электрона в прямоугольном потенциальном «ящике» с бесконечно высокими стенками сводится к решению уравнения: 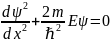при указанных краевых условиях (12.16). Запишем решение этого уравнение в виде: 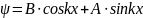, где к имеет смысл волнового числа волны де Бройля для электрона, находящегося внутри потенциального «ящика», А и В – постоянные. Используя первое из краевых условий (12.16), получим В=0 (так как cos0 0, а sin0=0). С учетом второго граничного условия получаем: . Отсюда следует, что В=0, А 0, sinka=0. (12.17)

Но sinka=0, когда kа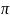=n , a k_n = 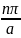, где n=1 ,2,3 (12.18)

Условие (12.18) имеет следующий физический смысл:

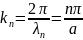, отсюда 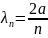, (12.19)

То есть на длине потенциального «ящика» должно укладываться целое число полуволн де Бройля.

Еще один важный вывод из условия (12.18): энергия Е электрона в потенциальном «ящике» не может быть произвольной. Она принимает лишь ряд дискретных собственных значений 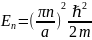, где n=1 ,2,3 и т.д. (12.20)

Для потенциального «ящика» с размерами а, соизмеримыми с размерами атома а=10^-9 м, собственные значения энергии электрона образуют последовательность энергетических уровней, «расстояние» между которыми 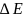= Е_n+1 - Е_n будет равно =(2n+1)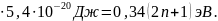

Для потенциального «ящика» с размером а=10^-2 м, соседние уровни отличаются друг от друга на величину

=(2n+1)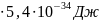 . Энергетические уровни в этом случае расположены так близко, что можно считать эти уровни как бы квазинепрерывными. Для такого потенциального «ящика» квантование энергии дает результаты, не столь существенно отличающиеся от результатов классической физики, чем в случае «ящика» атомного размера. Понятно, что 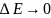, когда а , то есть энергетический спектр в этом случае будет непрерывным.

В общем случае, 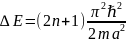или .

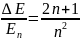Видно, что при увеличении квантового числа n, когда можно положить 2n+1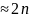 , отношение 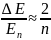и величина 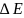становится малой по сравнению с Е_n , то есть происходит относительное сближение энергетических уровней. При больших квантовых числах n квантование энергии дает результаты, близкие к результатам классического рассмотрения.

Вероятность обнаружить внутри «ящика» электрон с энергией, отличной от 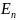, равна нулю. Физические величины, которые могут принимать лишь определенные дискретные значения, называются квантованными. Следовательно, энергия электрона, находящегося в потенциальном «ящике», квантуется. Квантованные значения Е_n называются уровнями энергии, а числа n, определяющие энергетические уровни электрона, называются квантовыми числами. Таким образом, электрон в потенциальном «ящике» может находиться только на определенном энергетическом уровне Е_n. Иногда говорят, что он находится в определенном квантовом состоянии n.

Условие нормировки в данной задаче принимает вид:

Учтем, что 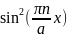= 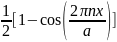и, взяв этот интеграл, получаем А= .

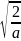В результате имеем конечное выражение для возможных решений уравнения Шредингера в поставленной задаче:

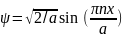, где n=1,2,3 . (12.21)

Данное решение показывает, что поведение электрона в одномерном бесконечно глубоком потенциальном «ящике» может быть различным в зависимости от значения числа n.

На рис. 12.2 представлены графики функций плотности вероятности нахождения частицы в бесконечно глубоком потенциальном «ящике» для n = 1, 2, 3. Горизонтальные, тонкие линии соответствуют значениям энергий состояний (энергетическая диаграмма или уровни возможных энергий системы), толстые линии соответствуют функции | ² .

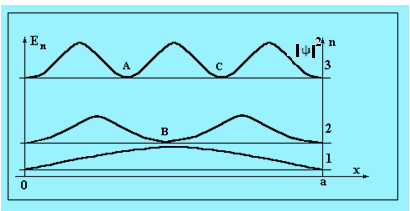
Рис. 12.2.

Из рисунка видно, что во втором и в третьем состояниях электрон не может находиться в некоторых точках «ящика» A,B,C, однако он может находиться между этими точками. Кроме этого, видно, что минимальное значение полной энергии Е₁, которая внутри «ящика» является кинетической энергией, не равна нулю, это означает, что частица находится в непрерывном движении. Такое поведение электрона существенно отличается от поведения макрочастиц, и приводит к тому, что в квантовой механике не может быть использовано классическое понятие траектории.