Министерство науки и высшего образования РФ

Федеральное государственное бюджетное образовательное

учреждение высшего образования

«Уфимский государственный авиационный технический университет»

Факультет информатики и робототехники

Кафедра вычислительной математики и кибернетики

Отчет по лабораторной работе №2

«Генерирование случайных процессов»

по дисциплине

«Компьютерное моделирование»

Выполнил:

студент группы МО-317

Ишпахтин А. А.

Проверила:

Валеева А. Ф.

Уфа 2021

Оглавление

Заключение 7

Задание:

Реализовать два алгоритма генерации случайных процессов: пуассоновский однородный и пуассоновский неоднородный. Проверить каждый на основе полученных данные по критерию согласия К. Пирсона принадлежность исследуемой случайной переменной пуассоновскому закону распределения.

Теоретические сведения:

1. Критерий согласия хи-квадрат К. Пирсона – это статистический критерий о том, что генеральная совокупность имеет распределение предполагаемого типа; позволяет оценить значимость различий между фактическим (выявленным в результате исследования) количеством исходов или качественных характеристик выборки, попадающих в каждую категорию, и теоретическим количеством, которое можно ожидать в изучаемых группах при справедливости гипотезы.

2. Метод программирования «сверху вниз» (или «нисходящее» программирование) – это один из двух основных подходов создания программ и алгоритмов, при которой разработка начинается с определения целей решения проблемы, после чего идет последовательная детализация, заканчивающаяся детальной программой. Является противоположной методике программирования «снизу вверх». При нисходящем проектировании задача анализируется с целью определения возможности разбиения ее на ряд подзадач. Затем каждая из полученных подзадач также анализируется для возможного разбиения на подзадачи. Процесс заканчивается, когда подзадачу невозможно или нецелесообразно далее разбивать на подзадачи. В данном случае программа конструируется иерархически - сверху вниз: от главной программы к подпрограммам самого нижнего уровня, причем на каждом уровне используются только простые последовательности инструкций, циклы и условные разветвления.

Ход работы:

1. Генерирование однородного пуассоновского процесса

• Алгоритм (символом ‘#’ обозначим комментарии кода):

• Вход: T # время окончания процессов, вещественное lambd( 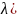# лямбда-параметр, вещественное N # количество данных, целое

• Выход: I # число событий, которые произойдут к моменту времени T, целое S(1), …, S(I) # времена событий в возрастающем порядке, вещественные (< ? >)

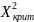
• Шаг 1. Ввести входные данные.

• Шаг 2. Инициализация промежуточных данных: S = [] # список времен событий t = 0 # начальное время I = 0 # число событий

• Шаг 3. Генерация первых времен:

while(t <= T): U = random(0, 1) t = t – 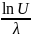I = I + 1 S[I] = t

• Шаг 4. Инициализируем список частот F (список целых чисел): step = T / N # шаг, вещественное for i = 1 to N F[i] = 0

• Шаг 5. Подсчитаем частоты F(список целых чисел):

for i = 1 to I

index = int(t/step)

F[index]=1+ F[index]

• Шаг 6. Задать список теоретических частот Т: for i = 1 to N P[i] = 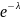* 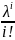Th[i] = I * P[i]

• Шаг 7. Считать значение Chi_Square: Chi_Square = 0 # инициализируем, вещественное for i = 1 to N Chi_Square = Chi_Square + / Th[i]

• Шаг 8. Сравнить полученное значение с табличным при вероятности ошибки 0.05 и степенью свободы N – 2: critical_value = (N – 2) if (Chi_Square < critical_value) output(‘Гипотеза принимается’) else output(‘Гипотеза НЕ принимается’)

2. 

   import random import math table_values = [0.05, 3.841, 5.991, 7.815, 9.488, 11.070, 12.592, 14.067, 15.507, 16.919, 18.307, 19.675, 21.026, 22.362, 23.685, 24.996] # 1. ввод входных значений T = float(input('Введите время окончания процессов: ')) lambd = float(input('Введите лямбду-параметр: ')) N = int(input('Введите количество интервалов времени: ')) # 2. инициализация промежуточных данных S = [] # список времен событий t = 0 # начальное время I = 0 # число событий while (t <= T): U = random.random() t -= math.log(U) / lambd I += 1 S.append(t) S.pop() I -= 1 # 3. подсчет количества точек в интервалах step = T / N # шаг разбиения F = [0 for _ in range(N)] # список счетчиков фактических частот for t in S: index = int(t / step) F[index] += 1 # 4. вычисление теоретических частот P = [math.exp(-lambd) * (lambd ** i) / math.factorial(i) for i in range(N)] # список вероятностей по Пуассону Th = [I * P[i] for i in range(N)] # список теоретических частот # 5. проверка по критерию Пирсона Chi_Square = sum([(F[i] - Th[i]) ** 2 / Th[i] for i in range(N)]) # хи-квадрат (наблюдаемое значение) critical_value = table_values[N - 2] # табличное критическое значение # 6. вывод (выходные значения) print(I) print(S) print(Chi_Square) print(critical_value) print(Chi_Square < critical_value)

   Код программы на языке программирования python

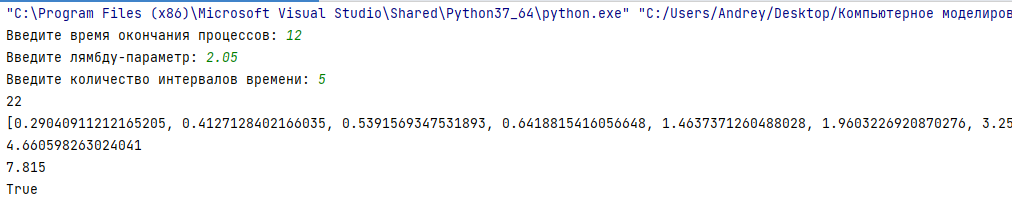
3. Пример генерирования однородного процесса

4. Генерирование неоднородного пуассоновского процесса

• Алгоритм(символом ‘#’ обозначим комментарии кода):

• Вход: T # время окончания процессов, вещественное lambd( # лямбда-параметр, вещественное N # количество данных, целое

• Выход: I # число событий, которые произойдут к моменту времени T, целое S(1), …, S(I) # времена событий в возрастающем порядке, вещественные (< ? >)

• Шаг 1. Ввести входные данные.

• Шаг 2. Инициализация промежуточных данных: S = [] # список времен событий t = 0 # начальное время I = 0 # число событий

• Шаг 3. Генерация первых времен, 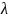(t)=|sin(t)| :

while(t <= T):

U1 = random(0, 1)

t = t -

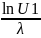
U2 = random(0, 1)

if U2 <= (t)/ :

I = I + 1

S[I] = t

• Шаг 4. Инициализируем список частот F (список целых чисел): step = T / N # шаг, вещественное for i = 1 to N F[i] = 0

• Шаг 5. Подсчитаем частоты F(список целых чисел):

for i = 1 to I

index = int(t/step)

F[index]=1+ F[index]

• Шаг 6. Задать список теоретических частот Т: for i = 1 to N P[i] = * Th[i] = I * P[i]

• Шаг 7. Считать значение Chi_Square: Chi_Square = 0 # инициализируем, вещественное for i = 1 to N Chi_Square = Chi_Square + / Th[i]

• Шаг 8. Сравнить полученное значение с табличным при вероятности ошибки 0.05 и степенью свободы N – 2: critical_value = (N – 2) if (Chi_Square < critical_value) output(‘Гипотеза принимается’) else output(‘Гипотеза НЕ принимается’)

5. 

   import random import math table_values = [0.05, 3.841, 5.991, 7.815, 9.488, 11.070, 12.592, 14.067, 15.507, 16.919, 18.307, 19.675, 21.026, 22.362, 23.685, 24.996] # 1. ввод входных значений T = float(input('Введите время окончания процессов: ')) lambd = float(input('Введите лямбду-параметр: ')) N = int(input('Введите количество интервалов времени: ')) # 2. инициализация промежуточных данных S = [] # список времен событий t = 0 # начальное время I = 0 # число событий while (t <= T): U1 = random.random() t -= math.log(U1) / lambd U2 = random.random() if U2 <= abs(math.sin(t)) / lambd: I += 1 S.append(t) # 3. подсчет количества точек в интервалах step = T / N # шаг разбиения F = [0 for _ in range(N)] # список счетчиков фактических частот for t in S: index = int(t / step) F[index] += 1 # 4. вычисление теоретических частот P = [math.exp(-lambd) * (lambd ** i) / math.factorial(i) for i in range(N)] # список вероятностей по Пуассону Th = [I * P[i] for i in range(N)] # список теоретических частот # 5. проверка по критерию Пирсона Chi_Square = sum([(F[i] - Th[i]) ** 2 / Th[i] for i in range(N)]) # хи-квадрат (наблюдаемое значение) critical_value = table_values[N - 2] # табличное критическое значение # 6. вывод (выходные значения) print(I) print(S) print(Chi_Square) print(critical_value) print(Chi_Square < critical_value)

   Код программы на языке программирования python

6. Пример генерирования неоднородного процесса

Заключение

В ходе данной лабораторной работы были запрограммированы два алгоритма для генерации случайного однородного пуассоновского процесса и для генерации случайного неоднородного пуассоновского процесса, а алгоритм также для проверки принадлежности числа событий в интервалах пуассоновскому закону распределения по критерию Пирсона.