Цель работы: Сгенерировать пары зависимых случайных чисел, с заданными математическим ожиданием, СКО и коэффициентом корреляции по следующему алгоритму:

Ход работы

1. Сгенерировать , ,… , случайных чисел [0;1].

2. Получит сумму S этих чисел.

3. Вычислить число x по следующей формуле 1:

,

(1)

где:

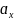• – математическое ожидание для x

• – среднеквадратическое отклонение для x

4. Вычислить число по следующей формуле 2:

,

(2)

где:

• – математическое ожидание для y

• – среднеквадратическое отклонение для y

• – коэффициент корреляции

5. Вычислить число по следующей формуле 3:

   =

   (3)

6. Сгенерировать 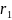, ,… , случайных чисел [0;1].

7. Получит сумму K этих чисел.

8. Вычислить число y по следующей формуле 4:

(4)

После генерации пар зависимых случайных чисел необходимо рассчитать для них математическое ожидание, СКО и коэффициент корреляции и сравнить их с введенными данными.

Для реализации данного алгоритма был использован Microsoft Excel, в котором был созданы следующие ячейки:

1. Созданы 6 столбцов B (рис.1) 6 столбцов R (рис.2) для генерации

случайных величин и 2 столбца для вычисления их суммы

Р исунок 1 – Столбцы B

Р исунок 2 – Столбцы R

Формула для получения случайных чисел: =СЛЧИС()*(0-1)+1

Р исунок 3 – Х теоретические и полученные значения

Х получ. (Мат. Ож.): =СРЗНАЧ(Расчеты!G2:G10001)

Х получ. (Ср. кв. откл.): =КОРЕНЬ(ДИСПР(Расчеты!G7:G10006))

Рисунок 4 – Y теоретические и полученные значения

Y получ. (Мат. Ож.): =СРЗНАЧ(Расчеты!L2:L10001)

Y получ. (Ср. кв. откл.): =КОРЕНЬ(ДИСПР(Расчеты!L2:L10001))

Рисунок 5 – RO теоретические и полученные значения

RO получ.: =СРЗНАЧ(C2:C10001)/(I4*T9)

2. С озданы 2 столбца для получения зависимых пар x и y представленные на рисунке 3

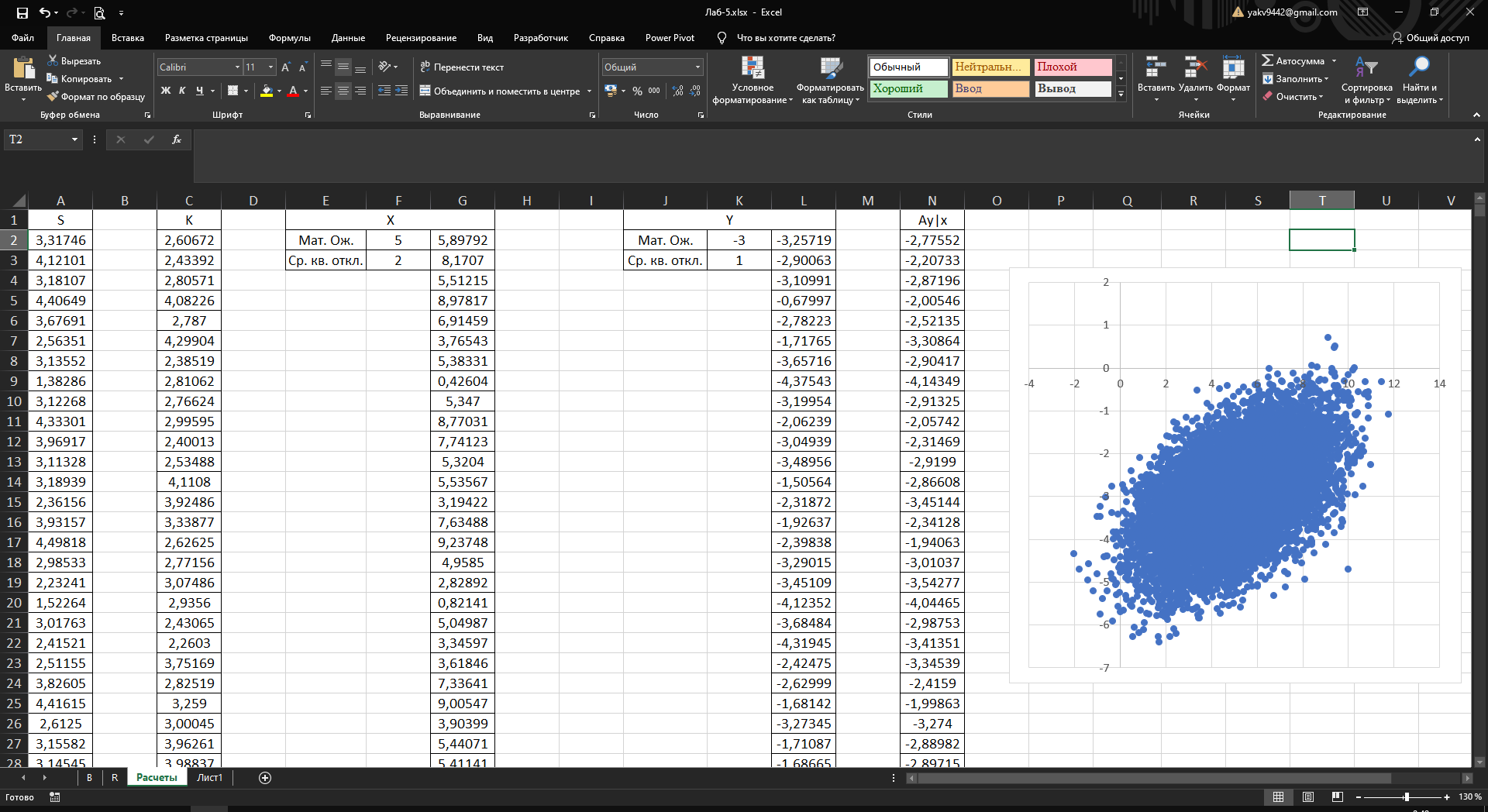
Рисунок 3 – Столбцы x и y

Для построения столбца Х использовалась формула:

=КОРЕНЬ(2)*$F$3*(A2-3)+$F$2

Для построения столбца Y использовалась формула:

=КОРЕНЬ(2)*Лист1!$I$9*(C2-3)+N2

3. Для анализа результатов была построен график, представленный на рисунке 4

Рисунок 4 – График для анализа результатов

Заключение

Из полученных результатов можно сделать вывод, что на основе приведенного алгоритма можно получить пары зависимых случайных чисел, с заданными параметрами, при чем их зависимость определяется значением коэффициента корреляции, при значении равному 0 зависимость отсутствует, при значении равному 1 зависимость линейная.