Ход работы

Воспользуемся методом критерия 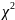для проверки псевдослучайной последовательности, сгенерированной посредством линейного конгруэнтного генератора с параметрами (1 -3).

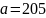(1)

(2)

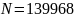(3)

Формула генератора представлена в 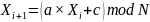(4).

(4)

Алгоритм проверки состоит из следующих шагов:

1. Генерация достаточно большой (n шт) псевдослучайной последовательности (в рамках данной работы – n = 279936 ед.).

2. Разбиение отрезка [0, N-1] на k = 100 интервалов (N – модуль генератора).

3. Подсчет количества элементов, попавших в интервал .

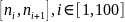4. Вычисление статистики по формуле (5), где S – номер интервала, 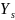– количество элементов последовательности, попавших в интервал S.

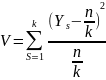(5)

5. Сравнение с экспериментального значения V с теоретическим значением .

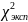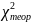В пункте 5 возможны три случая. Первый случай: много больше любого в строке — гипотеза о случайности равномерного генератора не выполняется (разброс чисел слишком велик, чтобы быть случайным). Второй случай: много меньше любого в строке — гипотеза о случайности равномерного генератора не выполняется (разброс чисел слишком мал, чтобы быть случайным). Третий случай: лежит между значениями двух рядом стоящих столбцов — гипотеза о случайности равномерного генератора выполняется с вероятностью p (то есть в p случаях из 100). Следует заметить, что чем ближе получается p к значению 50%, тем лучше.

В ходе данной работы был использован генератор, полученный в ходе лабораторной работы 1 и разработана программа на языке программирования C#, удовлетворяющая алгоритму проверки методом критерия (исходный код представлен в приложении А). Результат выполнения программы п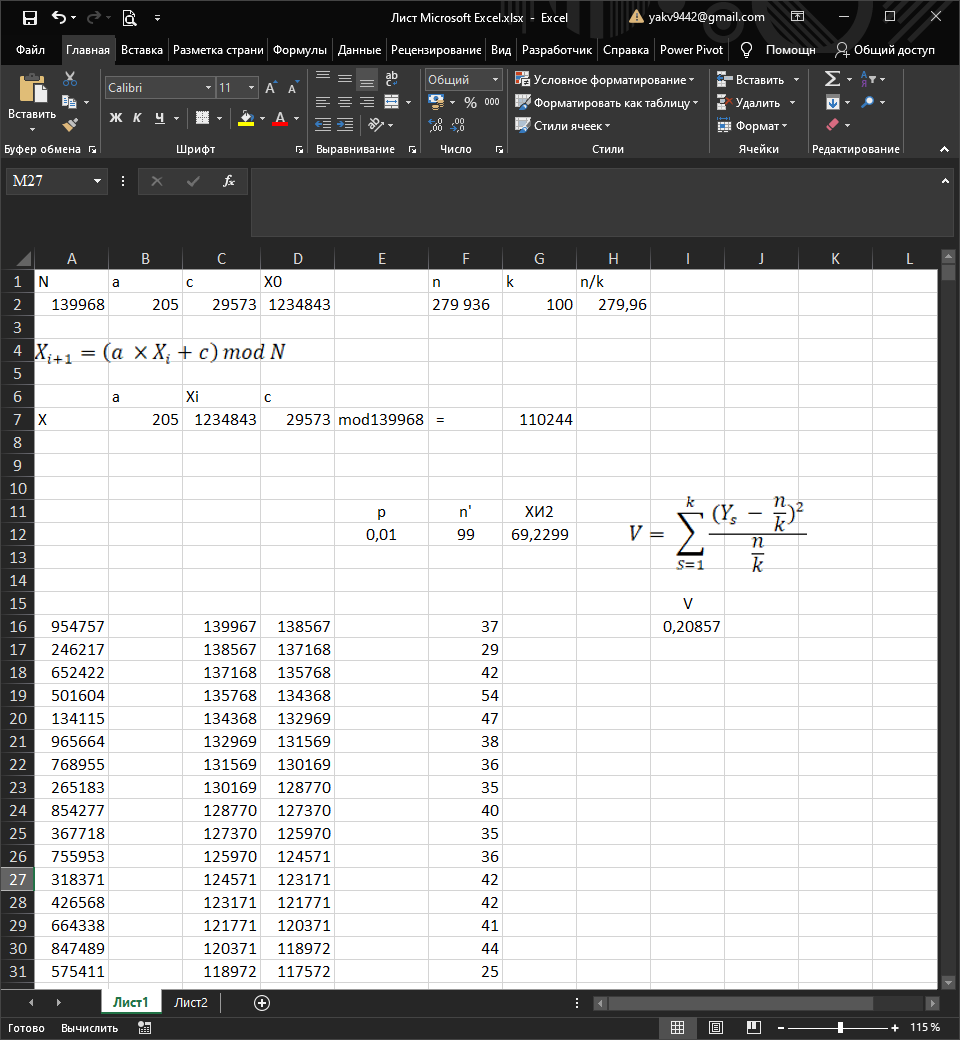 редставлен на рисунке 1.

Рисунок 1 – Результат работы программы

В результате было получено значение V = 0,20857. Его следует сравнить с теоретическим значением критерия, который можно получить в Excel по формуле 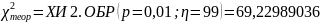, где p – это вероятность попадания в интервал (6), а 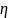– число степеней свободы (7).

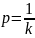(6)

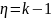(7)

Заключение

Исходя из полученных данных, можно сказать, что 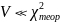, потому мы попадаем в случай 2: разброс чисел слишком мал, чтобы быть случайным. Следовательно, гипотеза о случайности генератора не выполняется.

В данной работе был получен практический опыт применения критерия для проверки псевдослучайной последовательности, была реализована в Microsoft Exel для автоматизации проверки больших последовательностей.