
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ ИНФОРМАТИКИ И РОБОТОТЕХНИКИ
КАФЕДРА ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ И КИБЕРНЕТИКИ
|
|
|
||
|
УТВЕРЖДАЮ Проректор университета по научной работе ФИО |
|||
|
|
|
||
|
"___" ______________ _______г. |
|||
|
|
|
||
Расчетно-графическая работа
«СМО с одним устройством» |
||||
|
||||
по предмету: КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ |
||||
Преподаватель |
|
А. Ф. Валеева |
||
|
|
|
||
|
|
|
||
|
|
|
||
Исполнитель |
|
А. Р. Шакиров |
||
|
|
|
||
Уфа - 2021 |
||||
ЗАДАНИЕ
Требуется разработать имитационную модель работы магазина «Рога и Копыта» с одной кассой. График работы магазина с 8 до 18, но продолжает работать до ухода последнего покупателя, в среднем в час прибывает 3 человека. Известно, что наибольшее количество посетителей приходит в первой половине дня.
Пусть Y – случайная переменная – время обслуживания устройства с распределением G.
• Клиенты прибывают в систему с одним устройством и одной очередью.
• Когда клиенты поступают в систему, они образуют очерет если устройство занято
• Когда обслуживание клиента завершается он покидает систему, и клиент, находящийся дольше всего в очереди, начинает обслуживаться.
Пояснения к модели:
1. Устройство обслуживания – касса;
2. Требования – покупатели;
3. Единица времени – час;
4. Интенсивность – 3 человека в час;
5.
Функция интенсивности λ
(t):

6. Время работы T – 10 часов (с 8 до 18);
Обеденный перерыв не учитывается (отсутствует / сменная работа), есть
вероятность переработки (последний клиент уйдет после закрытия магазина).
Оценки модели:
Оценка ожидаемой средней задержки клиентов в очереди:
 ,
,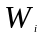 —
время задержки
клиента i
в
очереди,
—
время задержки
клиента i
в
очереди,
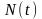 -
число клиентов, которые прибыли в период
времени
-
число клиентов, которые прибыли в период
времени
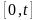
Оценку ожидаемого среднего числа клиентов в очереди:
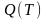 -
число клиентов в системе в период времени
-
число клиентов в системе в период времени
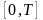 .
.

Оценка занятости устройства – ожидаемый коэффициент
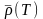 использования
устройства
(время, когда устройство занято/период
моделирования
T),
где функция
занятости В(t):
использования
устройства
(время, когда устройство занято/период
моделирования
T),
где функция
занятости В(t):
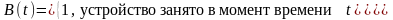

Среднее время, в течение которого клиент проводит в системе, вычисляется как:
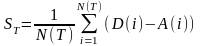 ,
,
где
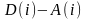 - это количество времени, в течение
которого клиент
- это количество времени, в течение
которого клиент
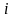 проводит
в системе;
проводит
в системе;
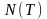 - общее число клиентов, которые пришли
до времени
- общее число клиентов, которые пришли
до времени
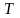 .
.
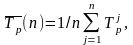
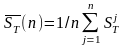 (оценки
для математических ожиданий
(оценки
для математических ожиданий
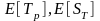 ,
имитация проводится
,
имитация проводится
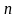 раз,
- достаточно велико).
раз,
- достаточно велико).
Описание модели
Вспомогательные функции
Функция интенсивности
Входные данные:
t – время в системе.
Выходные данные:
Значение функции интенсивности в момент времени t
Алгоритм:
1. Вернуть результат
Функция получения Пуассоновской случайной переменной относительно времени в системе или время первого прибытия после времени s
Входные данные:
s – время в системе,
λ – интенсивность.
Выходные данные:
t – время следующего события в системе.
Алгоритм:
1. Присвоить t = s.
2. Сгенерировать случайную переменную u1 = Uniform(0,1)
3.
Присвоить t =
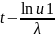
4. Сгенерировать случайную переменную u2 = Uniform(0,1), независимую от u1 .
5.
Если
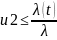 ,
,
5.1. то присвоить Tt = t
5.2. конец алгоритма
6. Иначе идти на шаг 2.
Функция генерации показательной случайной величины
Входные данные:
λ – интенсивность.
Выходные данные:
Y – значение показательной СВ
Алгоритм:
1. Сгенерировать случайное число U = Uniform(0,1).
2.
Возвратить величину Y =
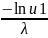
Процедуры работы смо
Случай 1. Следующее событие – прибытие клиента.
Условие возникновения:
tA ≤ tD и tA ≤ T
Входные данные:
T – время конца работы магазина относительно начала работы,
tA – время следующего прибытия клиента,
tD – время завершения работы устройства после обслуживания клиента,
NA – число приходов ко времени t,
ND – число уходов ко времени t,
n – длина очереди к моменту времени t.
Выходные данные:
NA – число приходов ко времени t,
t – время события (прибытия клиента),
tA – время следующего прибытия клиента,
tD – время завершения работы устройства после обслуживания клиента,
n – длина очереди к моменту времени t.
Алгоритм:
1. Присвоить: t = tA (движение вдоль оси времени ко времени tA)
2. Присвоить: NA = NA + 1 (подсчитано более одного прибытия к моменту времени tA)
3. Присвоить: n = n + 1 (в настоящее время имеется более одного клиента)
4. Генерировать Tt и присвоить tA = Tt (это время следующего прибытия клиента)
5. Если n=1, генерировать случайную переменную Y, имеющую показательное распределение и присвоить tD = t + Y
6. Запомнить выходные данные A(NA) = t (время прибытия клиента NA)
Случай 2. Следующее событие – уход клиента.
Условие возникновения:
TD ≤ tA и tA ≤ T
Входные данные:
T – время конца работы магазина относительно начала работы,
tD – время завершения работы устройства после обслуживания клиента,
NA – число приходов ко времени t,
ND – число уходов ко времени t,
n – длина очереди к моменту времени t.
Алгоритм:
1. Присвоить: t = tD
2. Присвоить ND = ND + 1(подсчитано более одного ухода клиента)
3. Присвоить: n = n – 1 (имеется меньше одного клиента)
4.
Если n
= 0, присвоить tD
=
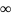
Иначе генерировать случайную величину Y, распределенную по показательному закону, и присвоить tD = t + Y
5. Запомнить выходные данные D(ND) = t (время ухода клиента ND)
Выходные данные:
ND – число уходов ко времени t,
t – время события (ухода клиента),
tD – время завершения работы устройства после обслуживания клиента,
n – длина очереди к моменту времени t.
Случай 3. Время работы закончилось, но остались необслуженные
клиенты.
Условие возникновения:
min(tD , tA ) > T и n > 0
Входные данные:
T – время конца работы магазина относительно начала работы,
tD – время завершения работы устройства после обслуживания клиента,
tA – время следующего прибытия клиента,
ND – число уходов ко времени t,
n – длина очереди к моменту времени t.
Выходные данные:
ND – число уходов ко времени t,
t – время события (ухода клиента),
tD – время завершения работы устройства после обслуживания клиента,
n – длина очереди к моменту времени t.
Алгоритм:
1. Присвоить: t = tD
2. Присвоить: ND = ND + 1(подсчитано более одного ухода клиента)
3. Присвоить: n = n - 1(имеется меньше одного клиента)
4. Если n >0, генерировать случайную переменную Y, распределенную по показательному закону и присвоить tD = t + Y
5. Запомнить выходные данные D(ND) = t
Случай 4. Время работы закончилось, клиентов в системе не осталось
Условие возникновения:
min(tD , tA ) > T и n = 0
Входные данные:
T – время конца работы магазина относительно начала работы,
tD – время завершения работы устройства после обслуживания клиента,
tA – время следующего прибытия клиента,
ND – число уходов ко времени t,
n – длина очереди к моменту времени t.
Выходные данные:
Tp – время окончания обслуживания последнего клиента, после закрытия.
Алгоритм:
1. Запомнить выходные данные Tp = max(t − T, 0)
Основная процедура
Входные данные:
T – время конца работы магазина относительно начала работы,
λ1 – интенсивность поступления клиентов,
λ2 – интенсивность времени обслуживания клиента.
Выходные данные:
A(i) – время прибытия клиента i,
D(i) – время ухода клиента i,
Tp – время после T, когда последний клиент уходит.
Алгоритм:
1.
Присвоить
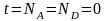
2.
Присвоить
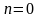
3.
Генерировать
![]() и присвоить
и присвоить
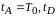 =
=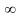
Изменения системы будут происходить в зависимости от того, какое из раннее определённых событий будет следующим:
- прибытие клиента,
- уход клиента,
- время работы закончилось, но остались необслуженные клиенты,
- время работы закончилось, клиентов в системе не осталось.
Анализ модели
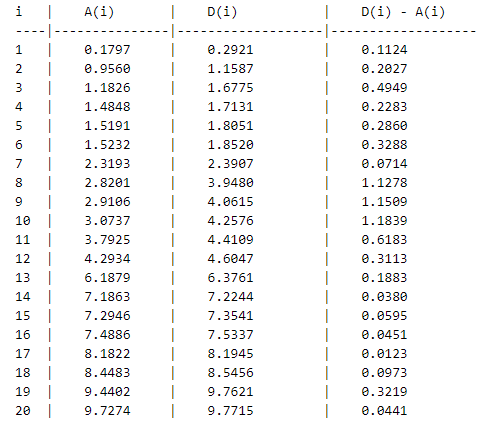
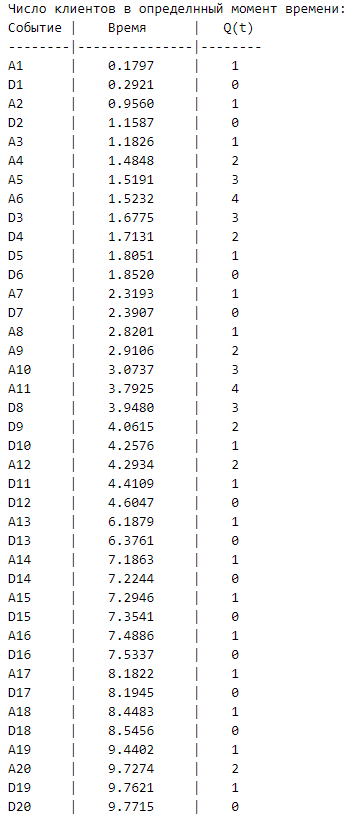
Результат работы модели:


Верификация имитационной модели
Для проверки правильности программы необходимо проверить выходные данные имитации с результатами, полученными вручную. В качестве примера возьмем среднее время, проведенное клиентами в системе St.
Во время работы программы были сохранены и выведены на экран события прихода и ухода клиентов.
Используя эти значения, а конкретно разность между уходом и приходом клиента (время, проведенное клиентами в системе) посчитаем среднее: (0.112+0.203+0.495+0.228+0.286+0.329+0.071+1.128+1.151+1.184+0.6183+0.311+0.188+0.038+0.06+0.045+0.012+0.097+0.322+0.044) / 20 = 0,34616
Программа показала результат St = 0,3462.
∆= |0,3462− 0,34611| = 0,00009 часов или же 324 миллисекунды. Расхождение появилось из-за погрешности округления.
Программа успешно прошла верификацию.
Оценка неизвестного параметра
Было проведено 10 прогонов имитационной модели, результаты представлены в таблице.
Требуется получить точечную оценку и приближенный (95%) доверительный интервал для ожидаемой средней задержки клиента в течение дня и доли клиентов, обслуженных после закрытия.
Результаты независимых повторных прогонов имитационной модели:
№ |
Число клиентов |
Время окончания обслуживания, ч |
Средняя задержка очереди, ч |
Средняя длина очереди |
Доля клиентов, обслуженных после закрытия |
1 |
20 |
9,77 |
0,166 |
1,256 |
0 |
2 |
21 |
9,91 |
0,041 |
0,946 |
0 |
3 |
26 |
9,84 |
0,133 |
1,211 |
0 |
4 |
33 |
9,93 |
0,091 |
1,148 |
0 |
5 |
26 |
9,40 |
0,136 |
1,161 |
0 |
6 |
25 |
10,357 |
0,027 |
0,810 |
1/25 = 0,04 |
7 |
21 |
10,004 |
0,051 |
0,903 |
1/21 = 0,05 |
8 |
21 |
9,79 |
0,022 |
0,76 |
0 |
9 |
25 |
10,045 |
0,083 |
0,945 |
1/25 = 0,04 |
10 |
26 |
10,161 |
0,057 |
0,926 |
1/26 = 0,038 |
Пусть
доверительная вероятность
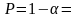
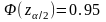 ,
по таблице значений функции
,
по таблице значений функции
 находится
находится
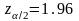 ,
уровень значимости
,
уровень значимости
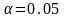 .
.
Вычислим среднюю задержку по формуле:
 ,
где
,
где
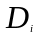 – задержка
–го
клиента
– задержка
–го
клиента
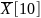 =
0,071
=
0,071
Вычислим среднеквадратичное отклонение:
S
=
 =
√0,003= 0,055
=
√0,003= 0,055
Рассчитаем доверительный интервал:
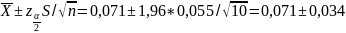
Можно утверждать с доверительной вероятностью в 95%, что средняя
задержка попадает в интервал [0,037; 0,105] ч.
Вычислим среднюю долю клиентов, обслуженных после закрытия:
 =
0,017
=
0,017
Вычислим среднеквадратичное отклонение:
S = = √0,000005= 0,0022
Рассчитаем доверительный интервал:
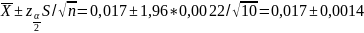
Можно утверждать с доверительной вероятностью в 95%, что доля клиентов, обслуженных после закрытия, попадает в интервал [0,0156; 0,0184].
Вывод
В ходе расчетно-графической работы была спроектирована модель работы магазина с одним устройством обслуживания.
На основе выходных данных были посчитаны оценки:
среднего времени, в течение которого клиент проводит в системе,
среднего времени после, когда уходит последний клиент,
ожидаемой средней задержки клиентов в очереди,
занятости устройства.
Также были проведены верификация модели и оценка неизвестного параметра.
