Коллок

1.Уравнение Шредингера в квантовой механике 

 

Общее уравнение Шредингера справедливо для любой частицы (со спином, равным 0), движущейся со скоростью малой по сравнению со скоростью света. Оно дополняется условиями, накладываемыми на волновую функцию:   

• волновая функция должна быть конечной, однозначной и непрерывной;  

• производные должны быть непрерывны;  

• функция   должна быть интегрируема; это условие в простейших случаях сводится к условию нормировки вероятностей.  

В тех случаях, когда частица находится в стационарных потенциальных силовых полях (энергия U=U(x,y,z) не зависит от времени), общее уравнение Шредингера можно упростить, исключив зависимость ψ от времени. 

2. Потенциальная энергия в атоме водорода 

Из уравнения движения электрона следует, что  кинетическая энергия равна потенциальной. Тогда можно записать:

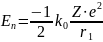
 Подставим сюда выражение для радиуса первой орбиты и получим:

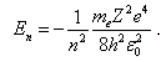
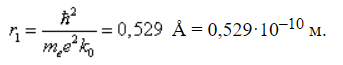
3. Собственное значение энергии электрона в атоме водорода

Полную информацию о возможных состояниях внешнего электрона в водородоподобных атомах можно получить, решив трехмерное уравнение Шредингера для стационарных состояний: где ψ – собственная волновая функция стационарного состояния, U – энергия кулоновского взаимодействия электрона с атомным ядром, Е – собственное значение энергии.

4. Волновая функция, отвечающая основному состоянию (1s -состоянию)

Волновая функция ψ, являясь основной характеристикой состояния микрочастицы, позволяет в квантовой механике вычислить средние значения физических величин, характеризующих данный микрообъект. Волновая функция – основной носитель информации о корпускулярных и волновых свойствах микрочастицы.

5. Волновая функция, отвечающая 2s состоянию

6. Первый боровский радиус

Радиус первой орбиты водородного атома называют боровским радиусом.

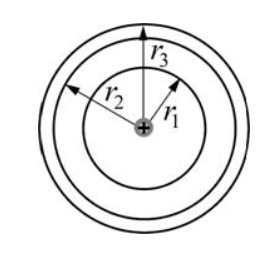
7. Вероятность обнаружить электрон в области, ограниченной элементом объема

Движение квантовой частицы отличается от движения классической частицы. В квантовой механике существует конечная вероятность обнаружить частицу в классически запрещённой области пространства.

Вероятность найти частицу в момент t в конечном объѐме V:

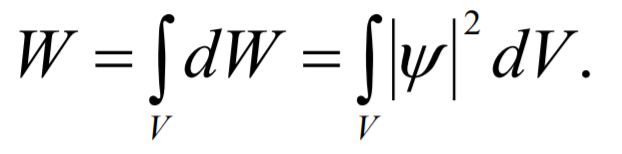
При интегрировании по бесконечному V вероятность обнаружить частицу равна 1. Из этого следует условие нормировки:

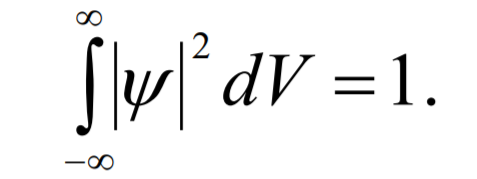
Все положения свободной частицы в пространстве равновероятны, т.к. вероятность обнаружить частицу в любой точке пространства

8. Состояние электронов в атоме однозначно определяется набором четырех квантовых чисел…

• главного n  ;

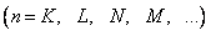• орбитального l   , обычно эти состояния обозначают 1s, 2d, 3f;

• магнитного m  ;

•  магнитного спинового

9. Принцип Паули:

в одном и том же атоме не может быть более одного электрона с одинаковым набором четырех квантовых чисел: n, l, m , m_s :

где Z (n, l, m , m_s ) - число электронов, находящихся в квантовом состоянии, описываемых набором четырех квантовых чисел: n, l, m , m_s . Таким образом, принцип Паули утверждает, что два электрона, связанные в одном и том же атоме различаются значениями, по крайней мере, одного квантового числа.

10. Максимальное число электронов находящихся в состоянии с данным n

      Максимальное число электронов, находящихся в состояниях, определяемых значением главного квантового числа n, равно:

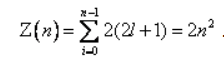
11. Максимальное число электронов находящихся в состоянии с данным l

Максимальное число  электронов, находящихся в состояниях, определяемых двумя квантовыми числами n и l:

12. Орбитальный момент импульса электрона

Момент импульса электрона в атоме квантуется

13. Проекция орбитального момента импульса электрона на направление внешнего магнитного поля

14. Магнитный момент импульса электрона

Орбитальный магнитный момент p_m, вызванный движением электрона по орбите обозначают L_m

Вектора L_l и L_m направлены в противоположные стороны.

L_m иногда обозначают μ_l .

15. Магнетон Бора

Это элементарный магнитный момент.

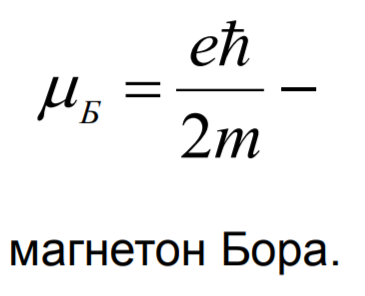
16. Проекция магнитного момента импульса электрона на направление внешнего магнитного поля

Проекция магнитного момента на направление внешнего магнитного поля (например, ось z): m_l – магнитное квантовое число, определяющее проекцию момента импульса электрона на z.

17. Собственный магнитный момент импульса электрона

Помимо собственного механического момента – спина, у электрона есть собсвенный магнитный момент, который связан с механическим соотношением:

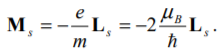
18. Проекция спинового магнитного момента импульса электрона на направление внешнего магнитного поля

Проекция магнитного момента спина на направление внешнего магнитного поля (например, ось z):

Электрон обладает собственным моментом импульса – спином, который не связан с движением электрона в пространстве и имеет только две ориентации относительно внешнего магнитного поля.