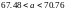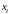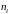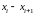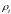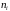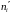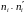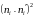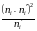Вар20_ОвчинниковА
.docxЗадача 1.
Решение. Найдём выборочную среднюю:
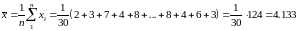
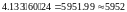
Ответ: В среднем мимо поста ГАИ за сутки проедет 5952 автомобиля.
Задача 2.
Решение. Даны 20 значений тока, найдём выборочную среднюю:
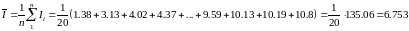
Средняя
мощность электрического тока
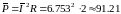
Ответ: 91.21
Задача 4.1. Дана выборка
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
13 |
8 |
9 |
11 |
15 |
9 |
8 |
5 |
13 |
9 |
Решение. Объём выборки
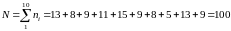
а)
Построим полигон. Отложим на оси абсцисс
варианты
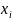 ,
а на оси ординат - соответствующие им
частоты
,
а на оси ординат - соответствующие им
частоты
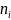 ,
соединив точки
,
соединив точки
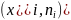 отрезками прямых, получим искомый
полигон частот.
отрезками прямых, получим искомый
полигон частот.
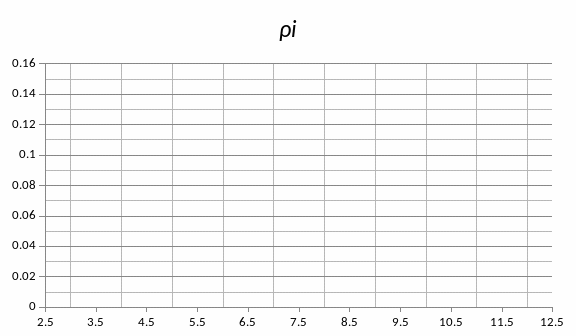
Построим
гистограмму относительных частот, для
этого запишем интервальный ряд и найдём
плотность относительной частоты
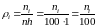 :
:
|
2,5; 3,5 |
3,5; 4,5 |
4,5; 5,5 |
5,5; 6,5 |
6,5; 7,5 |
7,5; 8,5 |
8,5; 9,5 |
9,5; 10,5 |
10,5; 11,5 |
11,5; 12,5 |
|
13 |
8 |
9 |
11 |
15 |
9 |
8 |
5 |
13 |
9 |
|
0,13 |
0,08 |
0,09 |
0,11 |
0,15 |
0,09 |
0,08 |
0,05 |
0,13 |
0,09 |
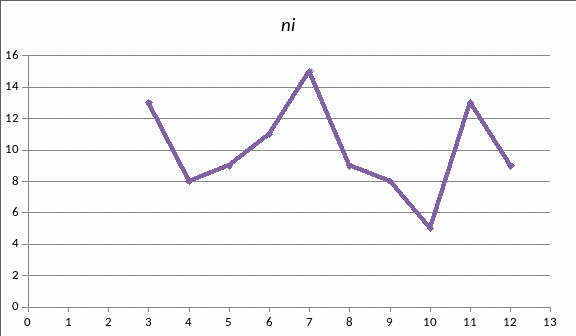
b) Найдём выборочную среднюю
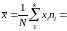
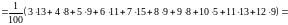
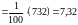
Найдём выборочную несмещённую оценку дисперсии
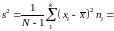
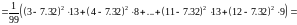
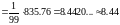
c) Теоретический закон равномерного распределения
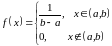
Параметры
 и
и
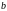 оценим по формулам:
оценим по формулам:
 ,
,
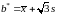 :
:
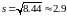
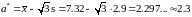 ,
,
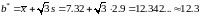 .
.
Предполагая,
что
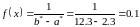 найдём теоретические частоты по формулам
найдём теоретические частоты по формулам
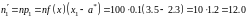
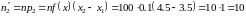
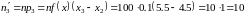 ,
,
Очевидно, что
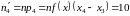
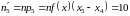
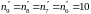
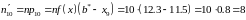
Прямая,
соответствующая функции плотности
вероятности
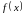 ,
проведена красной линией на гистограмме
относительных частот.
,
проведена красной линией на гистограмме
относительных частот.
d)Наблюдаемое значение критерия Пирсона вычисляется по формуле
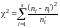
Здесь s=10 – число интервалов, на которые разбита выборка.
Результаты вычислений занесем в таблицу.
Интервалы |
Частота
|
Частота
|
|
|
|
2,5; 3,5 |
13 |
12 |
1 |
1,00 |
0,083 |
3,5; 4,5 |
8 |
10 |
-2 |
4,00 |
0,400 |
4,5; 5,5 |
9 |
10 |
-1 |
1,00 |
0,100 |
5,5; 6,5 |
11 |
10 |
1 |
1,00 |
0,100 |
6,5; 7,5 |
15 |
10 |
5 |
25,00 |
2,500 |
7,5; 8,5 |
9 |
10 |
-1 |
1,00 |
0,100 |
8,5; 9,5 |
8 |
10 |
-2 |
4,00 |
0,400 |
9,5; 10,5 |
5 |
10 |
-5 |
25,00 |
2,500 |
10,5; 11,5 |
13 |
10 |
3 |
9,00 |
0,900 |
11,5; 12,5 |
9 |
8 |
1 |
1,00 |
0,125 |
7,208
Вычислим
число степеней свободы
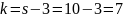 (s - число интервалов выборки). По таблице
значений хи-квадрат Пирсона при
(s - число интервалов выборки). По таблице
значений хи-квадрат Пирсона при
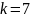 и уровне значимости
и уровне значимости
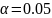 найдём критическое значение статистики
найдём критическое значение статистики
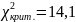
Так
как
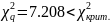 ,
то нет оснований отвергать гипотезу
о равномерном законе распределения.
,
то нет оснований отвергать гипотезу
о равномерном законе распределения.
Задача 5.
|
[0;1] |
[1;2] |
[2;3] |
[3;4] |
[4;5] |
[5;6] |
[6;7] |
[7;8] |
|
3 |
6 |
14 |
21 |
35 |
15 |
5 |
1 |
Решение.
Число вариант в выборке
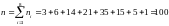
Для оценки математического ожидания служит доверительный интервал
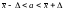 ,
,
где
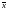 - выборочная средняя,
- выборочная средняя,
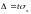 и
t есть такое значение аргумента функции
Лапласа
и
t есть такое значение аргумента функции
Лапласа
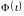 ,
при котором
,
при котором
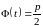 ,
,
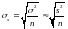 и
и
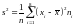
Вычислим выборочную среднюю:
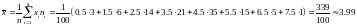 Вычислим
выборочную дисперсию:
Вычислим
выборочную дисперсию:

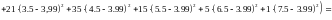
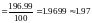
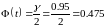 по
таблице находим
по
таблице находим
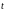 =1,96.
=1,96.
Находим
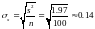 и
и
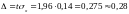
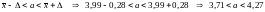
Доверительный
интервал для математического ожидания:
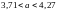
Ответ:
Задача 6.
Решение.
Для оценки математического ожидания
при известном
 служит доверительный интервал
служит доверительный интервал
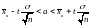 ,
,
t
есть такое значение аргумента функции
Лапласа
,
при котором
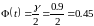 ,
по таблице находим
=1,64.
,
по таблице находим
=1,64.
Подставим
в формулу
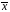 =69.12,
=69.12,
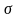 =10,
=10,
 =100
=100
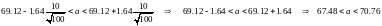
Ответ: