ПР3

Цели работы

а) освоение методов интерполяции функций;

б) совершенствование навыков по алгоритмизации и программированию вычислительных задач.

Постановка задачи

Составить схему алгоритма и программу на языке C/C++ решения задачи по теме «Интерполяция» в соответствии с индивидуальным заданием.

Вариант 5:

Значения

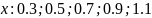
Значения

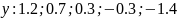
Метод интерполяции: Ньютона

Oписание метода интерполяции функций

Для интерполяции функций, заданных таблицами с равноотстоящими значениями аргумента

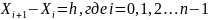
построение интерполяционных формул и вычисление по формулам заметно упрощается. В записях этих интерполяционных алгоритмов используются разности между значениями функции в соседних узлах интерполяции.

Конечной разностью первого порядка называется

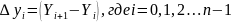
Из конечных разностей первого порядка образуются конечные разности второго порядка:

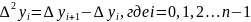
Аналогично определяются конечные разности третьего, четвёртого и более высоких порядков.

Для функций, заданных таблицами с постоянным шагом изменения аргумента, наиболее часто используются первая или вторая формулы Ньютона, в которых интерполяционная функция определяется как многочлен вида:

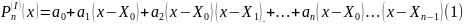
при интерполяции от нулевого узла 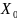или

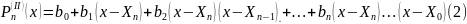
при интерполяции от узла .

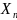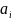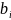Значения коэффициентов и в формулах (1) или (2) находятся из условий Лагранжа, определяющих в узлах интерполяции совпадение значений интерполирующей функции со значением табличнозаданной функции

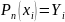
Полагая 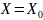, в формуле (1) получим

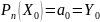
Аналогично для

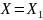
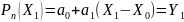
и далее

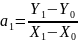
или, используя введённые обозначения,

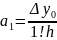
Продолжая подстановки значений Хi , получим

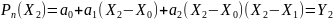
и далее

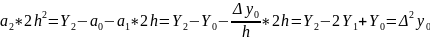
откуда

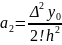
Проведя аналогичные преобразования для 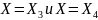, получим

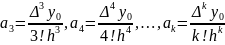
Найденные коэффициенты подставляются в формулы (1) или (2) для вычисления значений интерполируемой функции

На рисунке 2 представлен пример графика интерполирующей функции для узловых точек с координатами, которые представлены на рисунке 1.

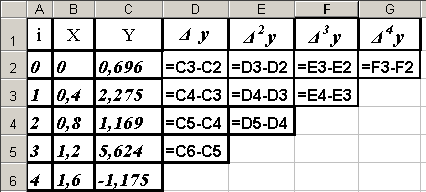
Рисунок 1 – Координаты узловых точек

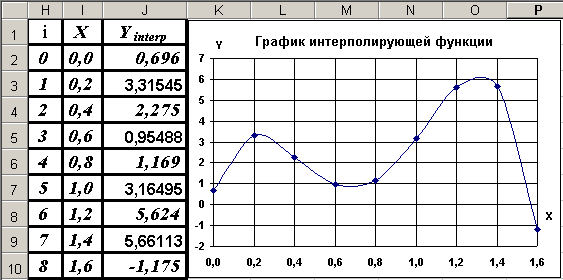
Рисунок 2 – График интерполирующей функции

Аналитический расчеты

На рисунках 3-7 представлены аналитические расчеты, выполненные с помощью онлайн-калькулятора.

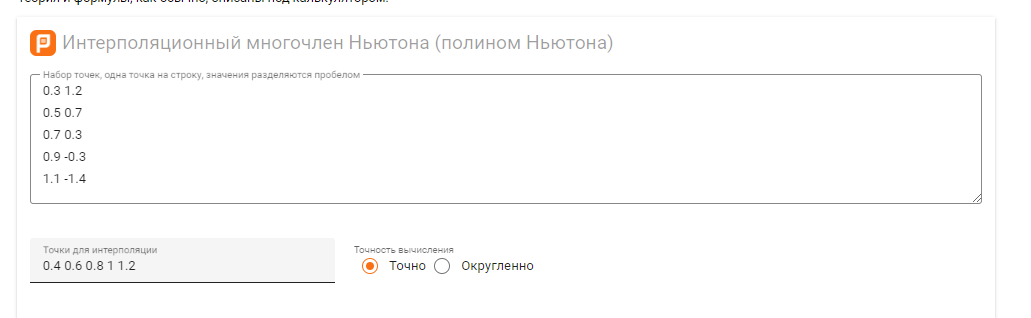
Рисунок 3 – Задание параметров для онлайн-калькулятора

Рисунок 4 – Результат интерполяции

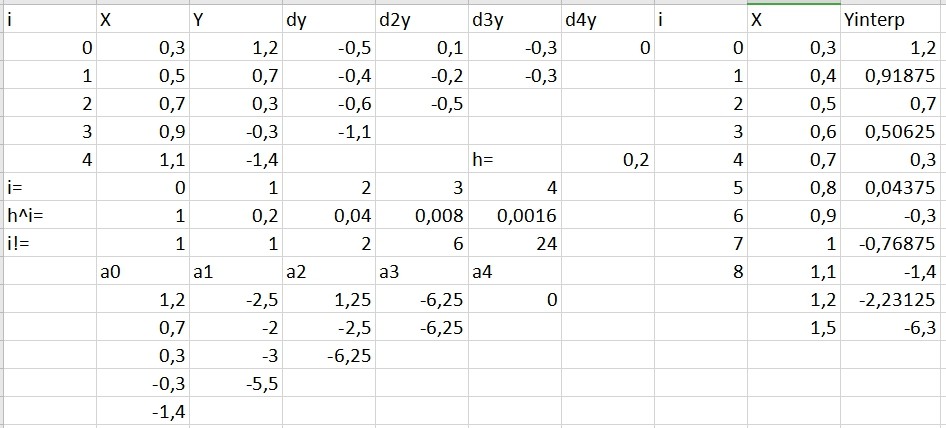
Рисунок 5 - Расчеты коэффициентов и значений полинома 

Рисунок 6 – Условные обозначения для графика интерполирующей функции

Рисунок 7 – График функции

Схема алгоритма решения задачи

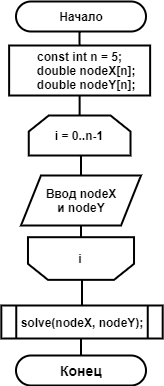
Рисунок 8 – Блох-схема функции main

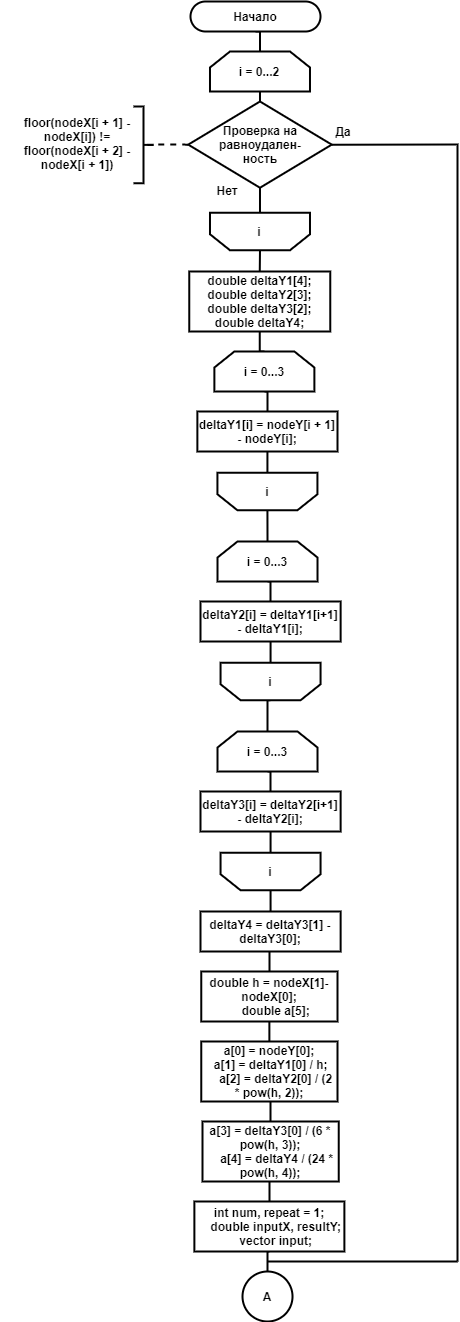
Рисунок 9 – Блок-схема функции solve (часть 1)

Рисунок 10 – Блок-схема функции solve (часть 2)

Текст программы

#include <iostream>

#include <vector>

using namespace std;

void solve(double nodeX[], double nodeY[]);

int main()

{

setlocale(LC_ALL, "rus");

const int n = 5;

double nodeX[n];

double nodeY[n];

cout << "Ввод координат узловых точек: \n";

for (int i = 0; i < n; i++) {

cout << "nodeX[" << i << "] = ";

cin >> nodeX[i];

cout << "nodeY[" << i << "] = ";

cin >> nodeY[i];

}

solve(nodeX, nodeY);

}

void solve(double nodeX[], double nodeY[]) {

//Проверка на равноудаленность значений nodeX

for (int i = 0; i < 3; i++) {

if (floor(nodeX[i + 1] - nodeX[i]) != floor(nodeX[i + 2] - nodeX[i + 1])) {

cout << "Ошибка значения nodeX не равноудалены руг от друга\n";

return;

}

}

//Вычисление конечных разностей

double deltaY1[4];

double deltaY2[3];

double deltaY3[2];

double deltaY4[1];

for (int i = 0; i < 4; i++) {

deltaY1[i] = nodeY[i + 1] - nodeY[i];

}

for (int i = 0; i < 3; i++) {

deltaY2[i] = deltaY1[i + 1] - deltaY1[i];

}

for (int i = 0; i < 2; i++) {

deltaY3[i] = deltaY2[i + 1] - deltaY2[i];

}

deltaY4[0] = deltaY3[1] - deltaY3[0];

//Вычисление значений коэффициентов полинома

double h = nodeX[1] - nodeX[0];

double a[5];

a[0] = nodeY[0];

a[1] = deltaY1[0] / h;

a[2] = deltaY2[0] / (2 * pow(h, 2));

a[3] = deltaY3[0] / (6 * pow(h, 3));

a[4] = deltaY4[0] / (24 * pow(h, 4));

int num, repeat = 1;

double inputX, resultY, mult;

vector <double> input;

while (repeat == 1)

{

//Ввод значений x

input.clear();

cout << "Введите количество точек: ";

cin >> num;

for (int i = 0; i < num; i++) {

cout << "x[" << i << "] = ";

cin >> inputX;

input.push_back(inputX);

}

//Вычисления y по первой формуле Ньютона

for (int i = 0; i < num; i++) {

mult = 1;

resultY = 0;

for (int j = 0; j < 5; j++) {

resultY += mult * a[j];

mult *= input[i] - nodeX[j];

}

cout << "resultY[" << i << "] = " << resultY << "\n";

}

cout << "\nВвести еще значения - 1, Выйти - 0\n";

cin >> repeat; }

}

Результаты программных расчетов

На рисунке 11 представлен результат работы программы.

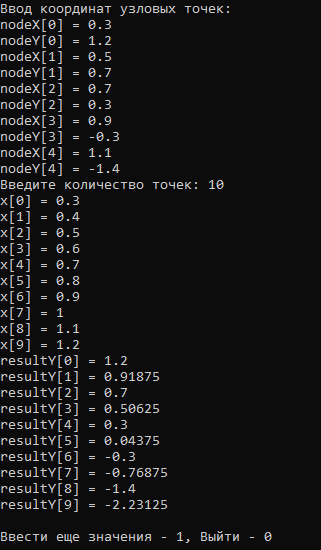
Рисунок 11 – Результат работы программы

Сравнение результатов программных и аналитических расчетов

В ходе тестирования программы выявлено, что полученные результаты совпадают с предсказанными в ходе аналитических расчетов с точностью до округления. Результаты интерполяции приведены на рисунках 3 - 6 для аналитического расчета и на рисунке 11 для программного расчета.

Выводы

В ходе выполнения практической работы был изучен метод Ньютона для интерполяции функции. Составлена схема решения поставленной задачи. Были аналитически предсказаны результаты работы программы с помощью онлайн-калькулятора. Так же была написана программа, позволяющая решать задачу интерполяции методом Ньютона. Полученные после работы программы результаты совпадают с аналитическими расчетами, следовательно программа работает корректно. При отладке ошибок не обнаружено.